A particle is dropped from point P at time t = 0. At the same time another particle is thrown from point O as shown in the figure and it collides with the particle P. Acceleration due to gravity is along the negative y-axis. If the two particles collide 2 s after they start, find the initial velocity v0 of the particle which was projected from O. Point O is not necessarily on ground.

√6m/s−1,θ=tan−1(1) with X-axis
√26m/s−1,θ=tan−1(5) with X-axis
√2m/s−1,θ=tan−1(2) with X-axis
√13m/s−1,θ=tan−1(4) with X-axis
The correct Answer is:B
x=(Ucosθ)t=2,Ucosθ=1
(Usinθ)t−12gt2=−10,Usinθ=5
V=√(Ucosθ)2+(Usinθ)2=√26,Tanθ=5
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level -V Multi answer18videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level -V Passage15videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - NCERT BASED QUES. PASSAGE8videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)24videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W29videos
MOTION IN A STRAIGHT LINE
Similar Questions
A particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?
 View Solution
View Solution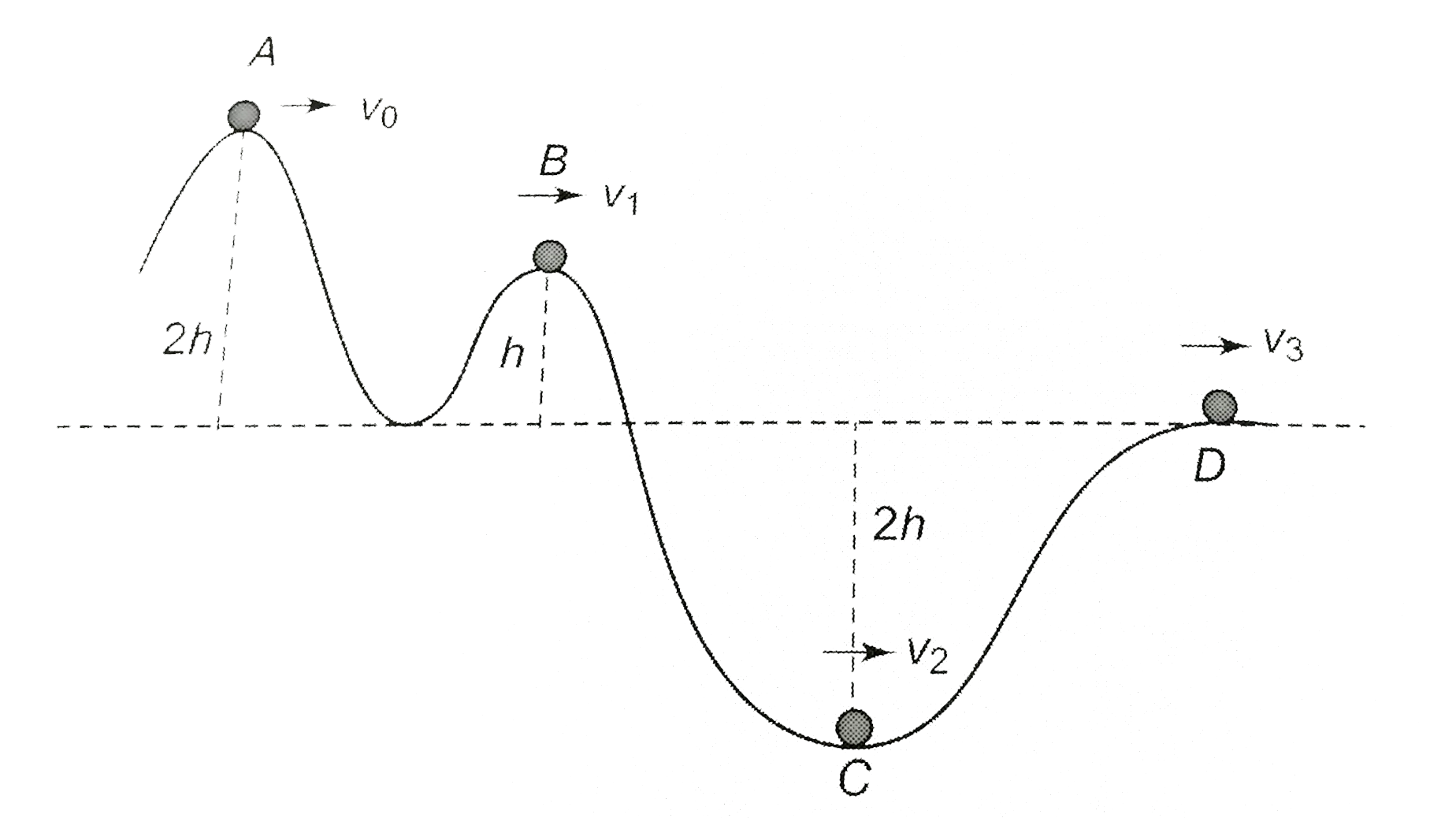
A particle is given velocity v0 at point A as shown in the figure. Find the speed of particle at point B,C and DView Solution
Knowledge Check
- Question 1 - Select One
A particle is dropped from a height 12 g metre and 4 s after another particle is projected from the ground towards it with a velocity 4gms−1 The time after which the second particle meets first is
A4 sB2 sC12sD1 s - Question 2 - Select One
A particle is dropped from a height 12 g metre and 4 s after another particle is projected from the ground towards it with a velocity 4gms−1 The time after which the second particle meets first is
A4 sB2 sC12sD1 s - Question 3 - Select One
Figure shows that particle A is projected from point P with velocity u along the plane and simultaneously another particle B with velocity v at an angle α with vertical. The particles collide at point Q on the plane. Then
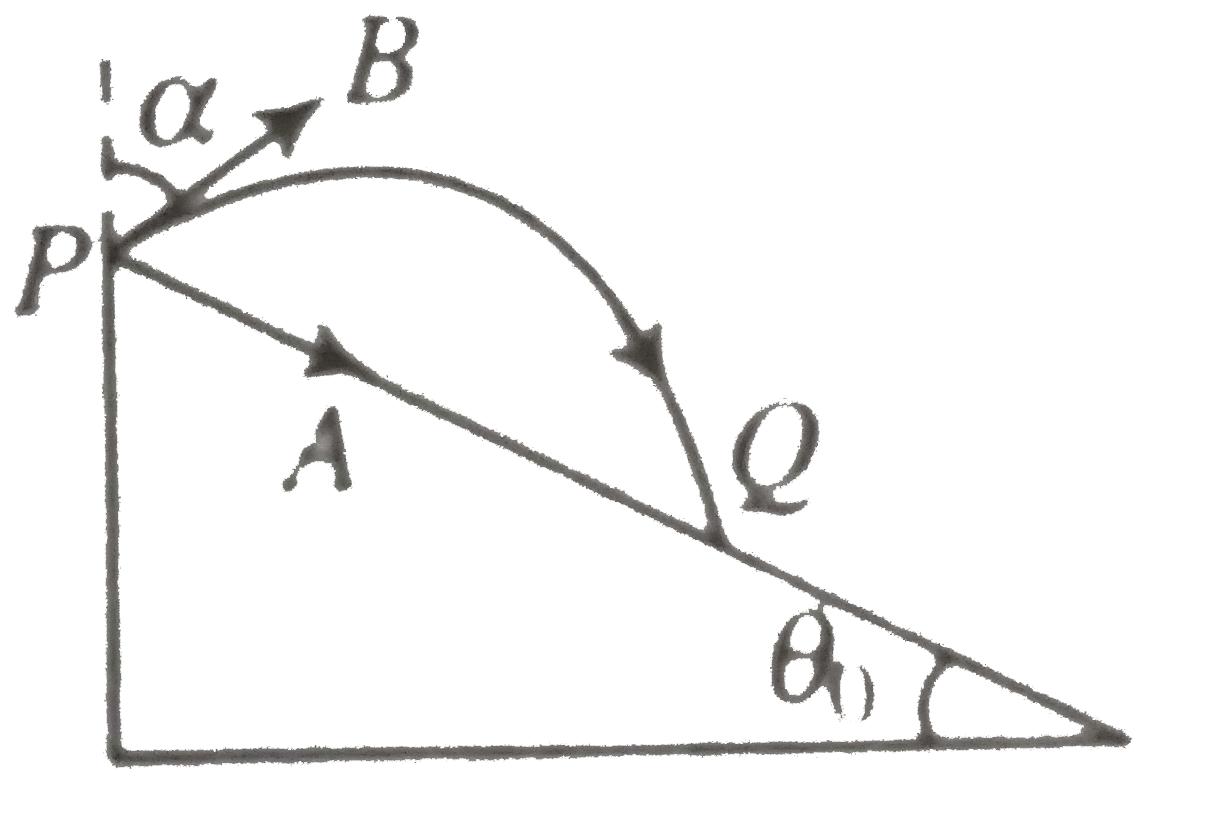 Avsin(α−θ0)=uBvcos(α−θ0)=uCv=uDNone of these
Avsin(α−θ0)=uBvcos(α−θ0)=uCv=uDNone of these
The acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.
 View Solution
View SolutionA particle P is moving along a straight line as shown in the figure. During the motion of the particle from A to B the angular momentum of the particle about O
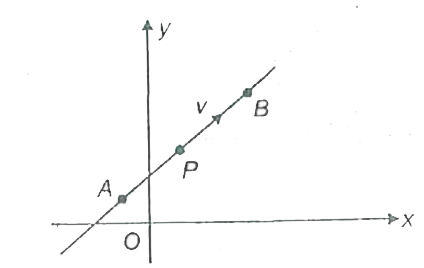 View Solution
View SolutionA graph of acceleration versus time of a particle starting from rest at t=0 is as shown in figure. The speed of the particle at t=14s is
 View Solution
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
View SolutionThe acceleration of particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be.
View Solution

