The coordinate of a particle moving in a plane are given by $x (t) = a cos (p t) and y (t) = b sin (p t)$ where $a, b (< a)$ and $P$ are positive constants of appropriate dimensions . Then

A

The path of the particle is an ellipse

B

The velocity and acceleration of the particle are normal to each other at $t = \frac{π}{2 p}$

C

The acceleration of the particle is always directed towards a fixed position

D

The distance travelled by the particle in time internal $t = 0$ to $t = \frac{π}{2 p}$ is $a$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C

$\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ ,So the path is an ellipse
$V_{x} = - a p sin p t, V_{y} = b p cos p t$
$a_{x} = - a p^{2} cos p t a_{y} = - b p^{2} sin p t$
So $\to V - \to a = 0$ when $\to V ⊥ \to a$
So $a^{2} p^{3} sin p t . cos p t - b^{2} p^{3} sin p t . cos p t$
$\Rightarrow a^{2} p^{3} sin p t . cos p t - b^{2} p^{3} sin p t . cos p t$
as $a \neq b$ So $sin$ pt. $cos p t = 0$
$\Rightarrow sin p 2 t = 0 \Rightarrow, 2 π \Rightarrow t = \frac{π}{2 P} - -$
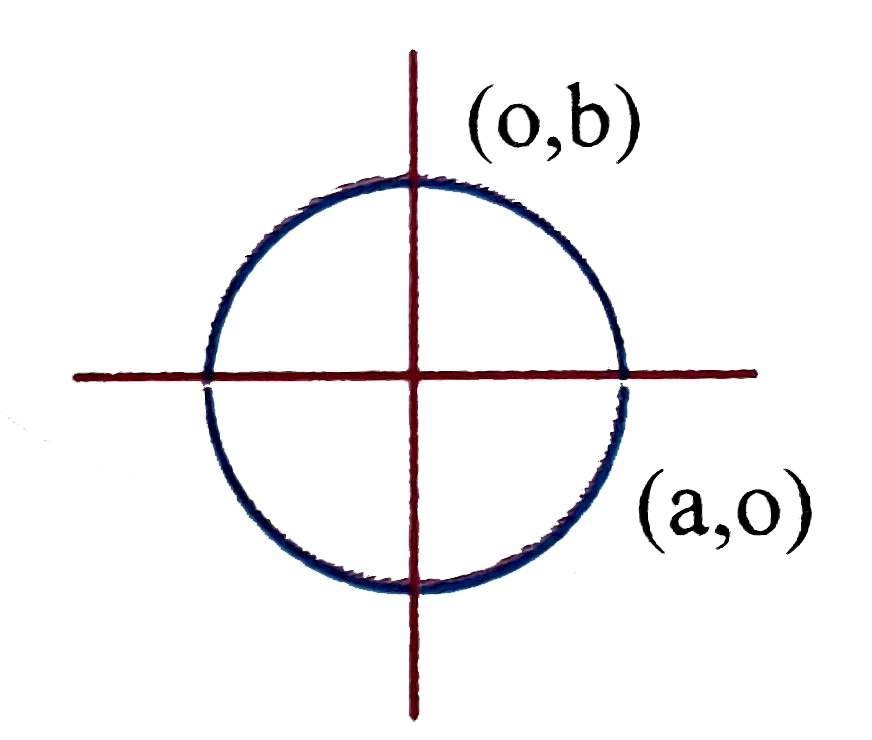
The motion is similar to motion of earth around sun So force always towards focus and hence acceleration. At $t = 0$ particle is at $(a, o)$
At $t = \frac{π}{2 p}$ particle is at $(o, b)$
So distance travelled along $X$ axis is a not the actual distance, which is the length of the part of the elipse between $(a, o)$ to $(o, b)$ you can try out for distance by following method $d s = \sqrt{{d x}^{2} + {d y}^{2}}$
$\Rightarrow d s = \sqrt{1 + {(\frac{d y}{d x})}^{2}} \Rightarrow \int_{0}^{s} = \int_{a}^{0} \sqrt{1 + {(\frac{d y}{d x})}^{2}} . (d x)$

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
The coordinates of a particle moving in a plane are given by $x (t) = a cos (p t) and y (t) = b sin (p t) where a, b (< a) and p$ are positive constants of appropriate dimensions. Then
Athe path of the particle is an ellipse.
Bthe velocity and acceleration of the particle are normal to each other at $t = π / (2 p)$ .
Cthe acceleration of the particle is always directed toward a focus.
Dthe distance traveled by the particle in time interval t = 0 to $t = π / (2 p)$ is a.
Question 2 - Select One
The coordinates of a moving particle at any time t are given by x = ct and y = bt. The speed of the particle at time t is given by
A2t(c-b)
B $\sqrt{(c^{2} + b^{2})}$
C $2 t \sqrt{(c^{2} + b^{2})}$
D $2 t \sqrt{(c^{2} + b^{2})}$
Question 3 - Select One
The coordinates of a moving particle at any time t are given by $x = c t$ and $y = b t^{2}$ . The speed of the particle is given by
A $2 t \sqrt{b^{2} - c^{2}}$
B $\sqrt{4 b^{2} t^{2} + c^{2}}$
C $2 t (b + c)$
D $2 t (b - c)$

NARAYNA-MOTION IN A PLANE-Level -V Multi answer

Home
Ask Doubt
Profile