A man in a boat crosses a river from point A. If he rows perpendicular to the banks he reaches point C (BC=120m) in 10 min. If the man heads at a certain angle α to the straight line AB (AB is perpendicular to the banks) against the current he reaches point B in 12.5 min. Find the width of the river w, the rowing velocity u, the speed of the river current v and the angle α. Assume the velocity of the boat relative to water to be constant and the same magnitude in both cases.

The width of the river is 300m
The width of the river is 200m
The rowing velocity is 20m/min
The rowing velocity is 30m/min
The correct Answer is:B, C
In the first case BC=vt1 and w=ut1.In the second caste usinα=v and w=ucosα12
Solving these four equations with proper substitution, we get w=200m,u=20m/min,v=12m/min and α≅37∘

Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level -V Passage15videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Integer6videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level -V Single answer31videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)24videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W29videos
MOTION IN A STRAIGHT LINE
Similar Questions
A man crosses a river in a boat. If he cross the river in minimum time he takes 10min with a drift 120m. If he crosses the river taking shortest path, he takes 12.5min, find
(a) width of the river
(b) velocity of the boat with respect to water
(c) speed of the currentView SolutionA man swimming in a river from a point. A on one bank has to reach a point C on other bank, which is at a distance l from the point B, directly opposite to A on other bank. River width is d and the current velocity is u0. Find the minimum speed of swimmer relative to still water with which he should swim.
View Solution
Knowledge Check
- Question 1 - Select One
A man in a boat crosses a river from point A. if the rows perpendicu lar to the bank he reaches point C(BC=120m) in 10 minutes. If the the man heads at a certain angle α to the straight line AB(AB is perpendicualr to the banks) against the current be reaches point B in12.5 minutes.
 Athe width of the river is 300mBthe width of the river is 200mCthe rowing velocity is 20m/minDthe rowing velocity is 30m/min.
Athe width of the river is 300mBthe width of the river is 200mCthe rowing velocity is 20m/minDthe rowing velocity is 30m/min. - Question 2 - Select One
A man is boat intends to cross river from A. If he rows perpendicular to the banks then he takes t1 = 10 minutes to reach the other bank and he reaches point C at a distance l = 120 m down the stream from the point B which is exactly opposite to A on the other bank. If he heads at a certain angle α to the straight path AB against the current he will reach point B in t2 = 12.5 minutes.
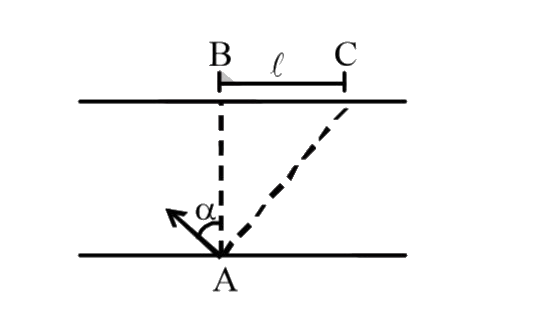
The width of river is-A180 mB200mC220 mDnone of these - Question 3 - Select One
A man crosses a 320m wide river perpendicular to the current in 4 min. If in still water he can swim with a speed 5/3 times that of the current, then the speed of the current, in m/min is
A30B40C50D60
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30oand 45o, respectively. If the bridge is at a height of 3 m from the banks, find the width of the river.
View SolutionThe speed of a swimmer with respect to the water is v, the speed of the stream is u. In what direction should the swimmer move to reach the opposite point on the other bank of the river? How long will he swim if the width of the river is l?
View SolutionA man wishes to cross a river to an exactly opposite point on the other bank. if the can swim with twice the velocity of the current, the inclination to the current of the direction he should swim is
View SolutionA man swims from a point A on the bank of a river if width 100m. When he swims perpendicular to the water current, he reaches the other bank 50m downstream. The angle to the bank at which he should swim, to reach the directly opposite point B on the other bank is.
 .View Solution
.View SolutionA man in a row boat must get from point A to point B on the opposite bank of the river (see figure).The distance BC=a.The width of the river AC=b.At what minimum speed u relative to the still water should the boat travel to reach the point B?The velocity of flow of the river is v0
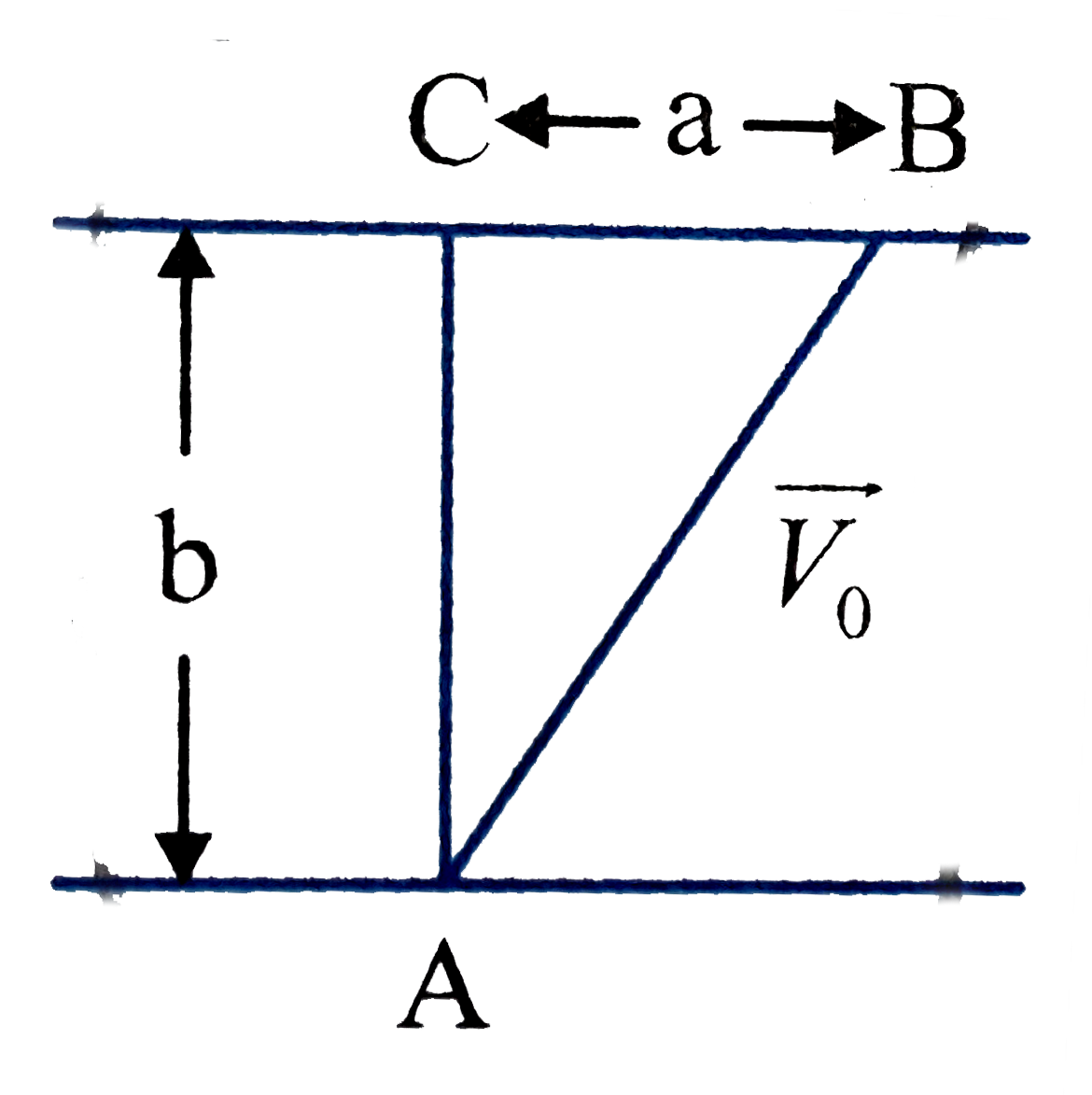 View Solution
View Solution

