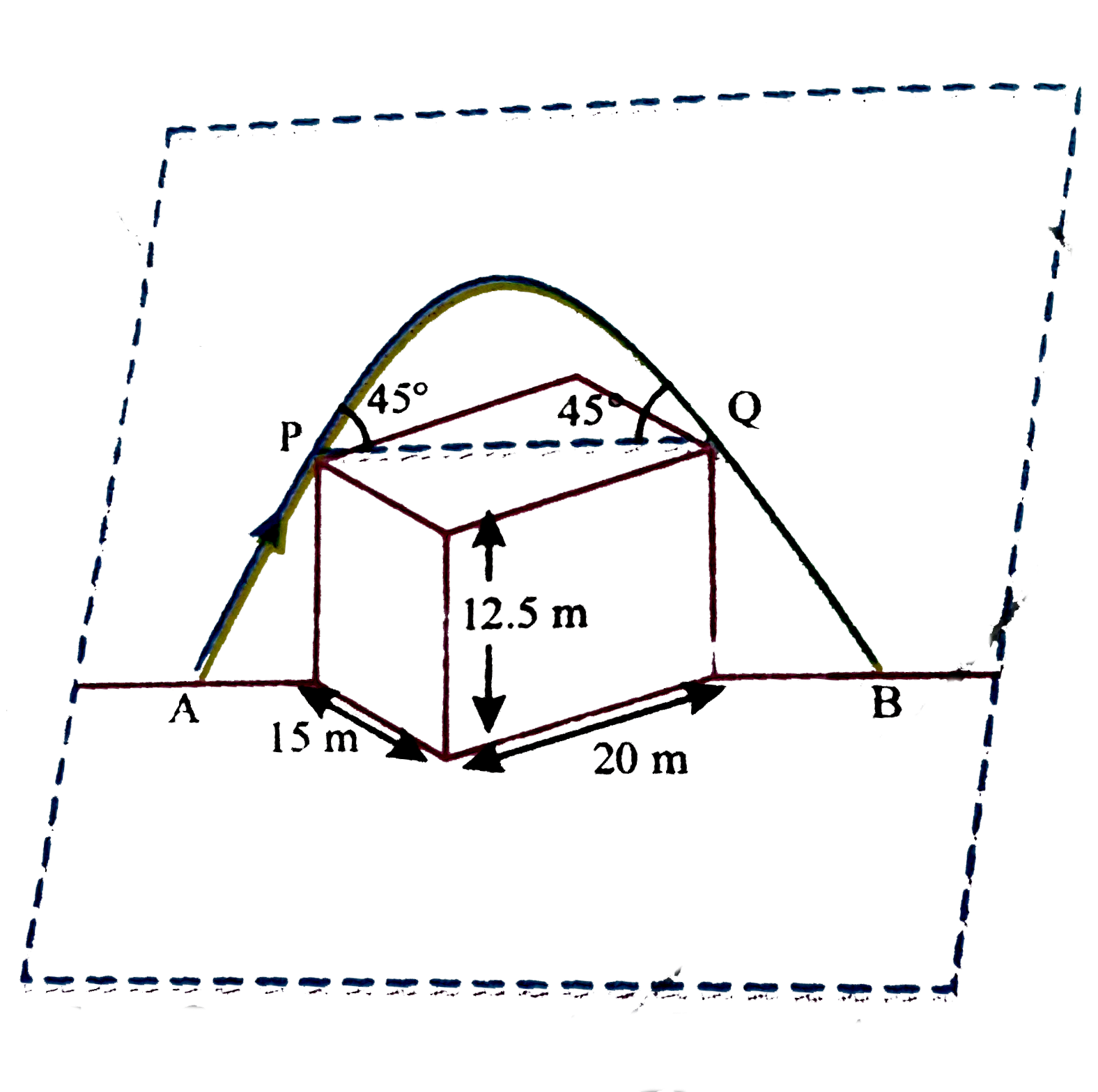
A particle is fired from A in the diagonal plane of a building of dimension 20m(length) × 15m (breadth) × 12.5m(height), just clears the roof diagonally & falls on the other side of the building at B.It is observed that the particle is travelling at an angle 45∘ with the horizontal when it clears the edges P and Q of the diagonal. Take g=10m/s2.
The speed of the particle at point P will be:
5√10m/s
10√5m/s
5√15m/s
5√5m/s
The correct Answer is:A
PQ length , U2sin2θg=25,U=5√10m/s
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Integer6videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-Vi single answer30videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level -V Multi answer18videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)24videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W29videos
MOTION IN A STRAIGHT LINE
Similar Questions
Knowledge Check
- Question 1 - Select One
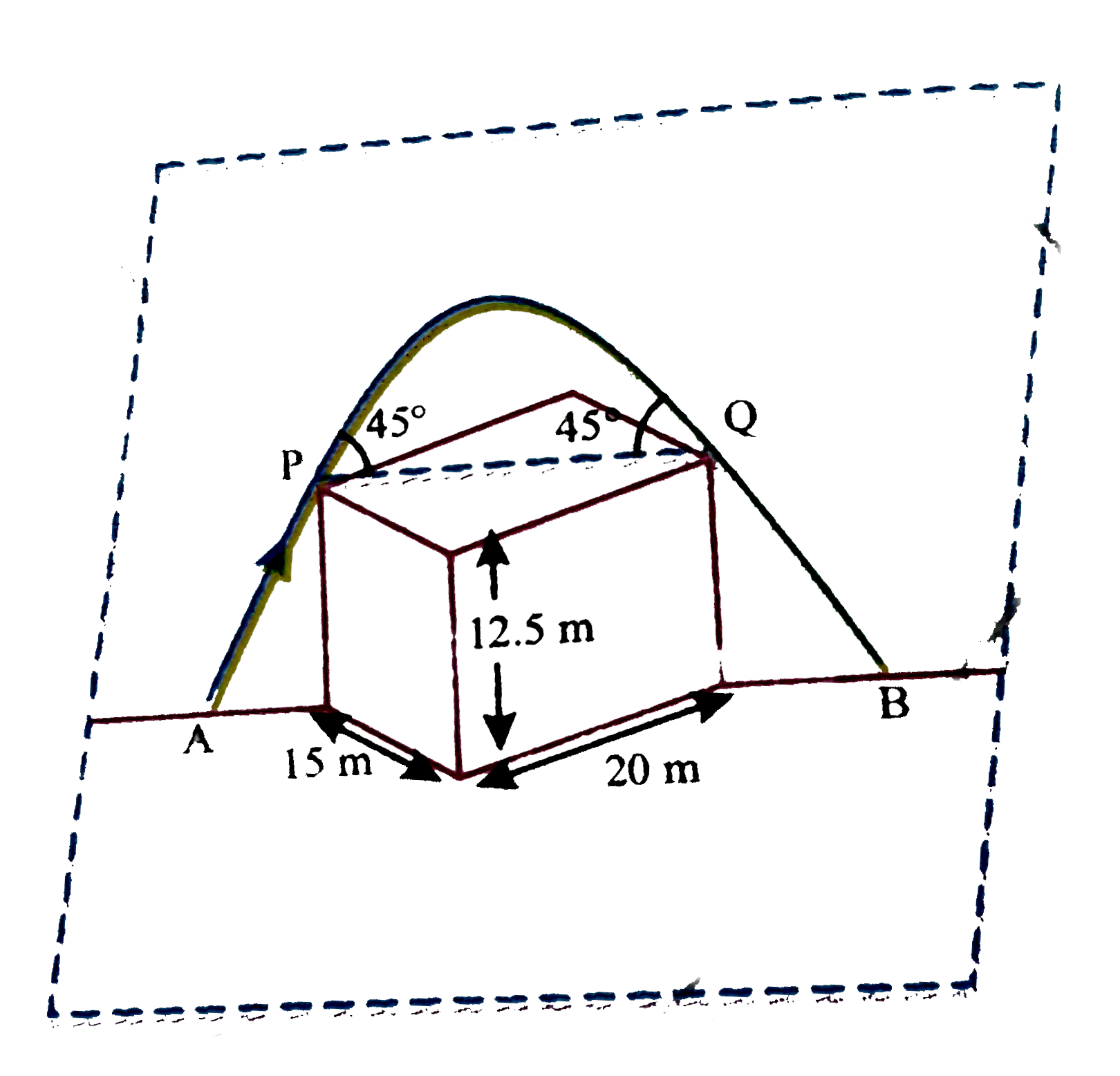
A particle is fired from A in the diagonal plane of a building of dimension 20m(length) × 15m (breadth) × 12.5m(height), just clears the roof diagonally & falls on the other side of the building at B.It is observed that the particle is travelling at an angle 45∘ with the horizontal when it clears the edges P and Q of the diagonal. Take g=10m/s2.
The speed of projection of the particle at A will be:
 A5√10m/sB10√5m/sC5√15m/sD5√5m/s
A5√10m/sB10√5m/sC5√15m/sD5√5m/s - Question 2 - Select One
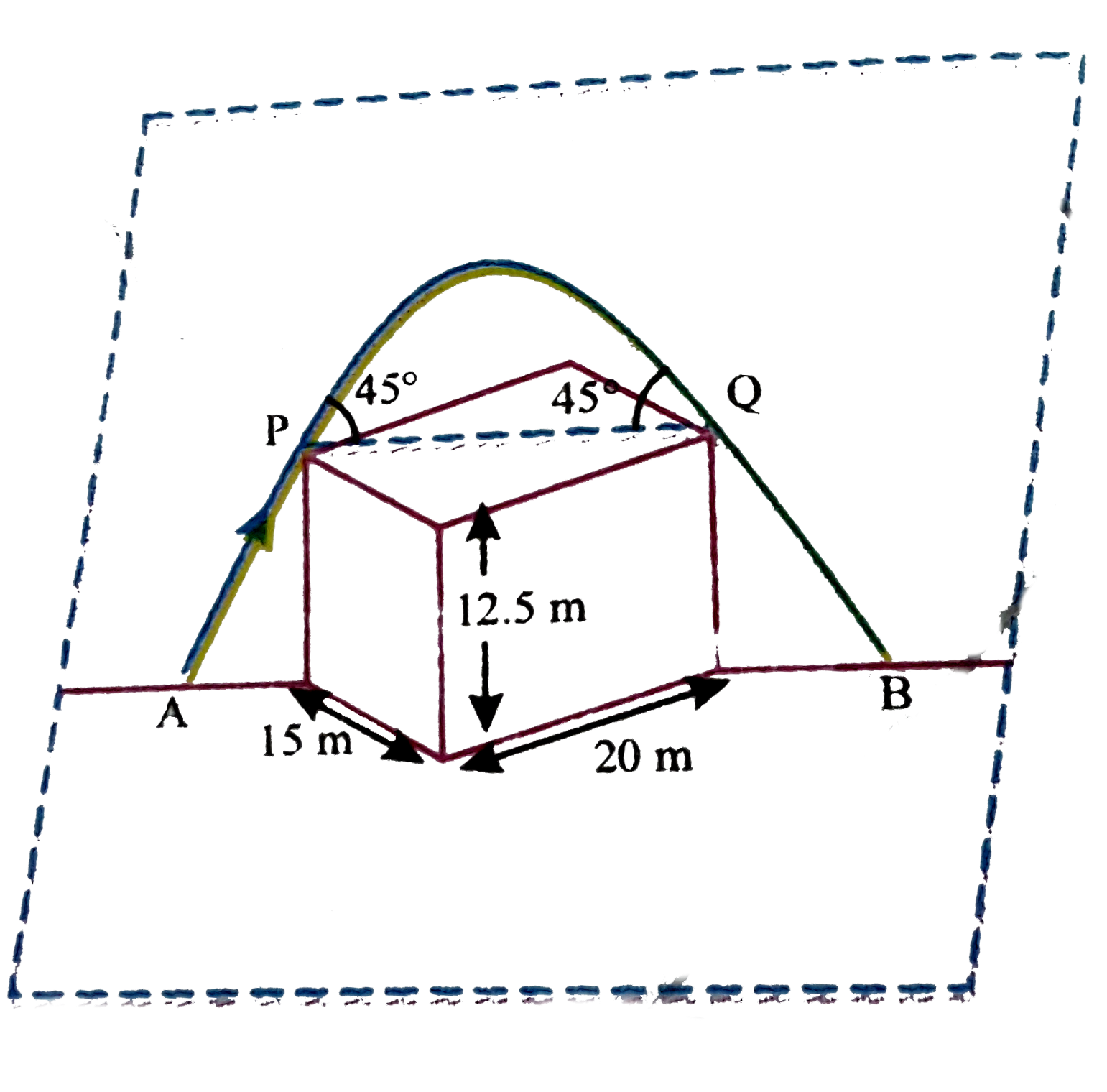
A particle is fired from A in the diagonal plane of a building of dimension 20m(length) × 15m (breadth) × 12.5m(height), just clears the roof diagonally & falls on the other side of the building at B.It is observed that the particle is travelling at an angle 45∘ with the horizontal when it clears the edges P and Q of the diagonal. Take g=10m/s2.
The range that is AB will be:
 A5√10mB25√3mC5√15mD25√5m
A5√10mB25√3mC5√15mD25√5m - Question 3 - Select One
A particle is fired from 'A' in the diagonal plane of a building of dimension 20m (length)×15m (breath) xx12.5m (height), just clears the roof diagonally and falls on the other side of the building at B. It is observed that the particle is travelling at an angle 45∘ with the horizonal when it clears the edges P and Q of the diagonal. Take g=10m/s2.

The speed of the particle at point P will be:A5√10m/sB10√5m/sC5√15m/sD5√5m/s
A commander fires a shell at certain angle of projection from A which clears the building of dimensions 20×15×12.5m in it's diagonal plane. Shell just clears the roof diagonally at points P and Q and falls on the other side of the building at B and makes angle 45∘ with the horizontal at P and Q as shown in the figure. If the range AB of the shell is a2×√b then find b? (a and b lowest possible integers)
 View Solution
View SolutionA particle is fired from 'A' in the diagonal plane of a building of dimension 20m (length)×15m (breath) xx12.5m (height), just clears the roof diagonally and falls on the other side of the building at B. It is observed that the particle is travelling at an angle 45∘ with the horizonal when it clears the edges P and Q of the diagonal. Take g=10m/s2.
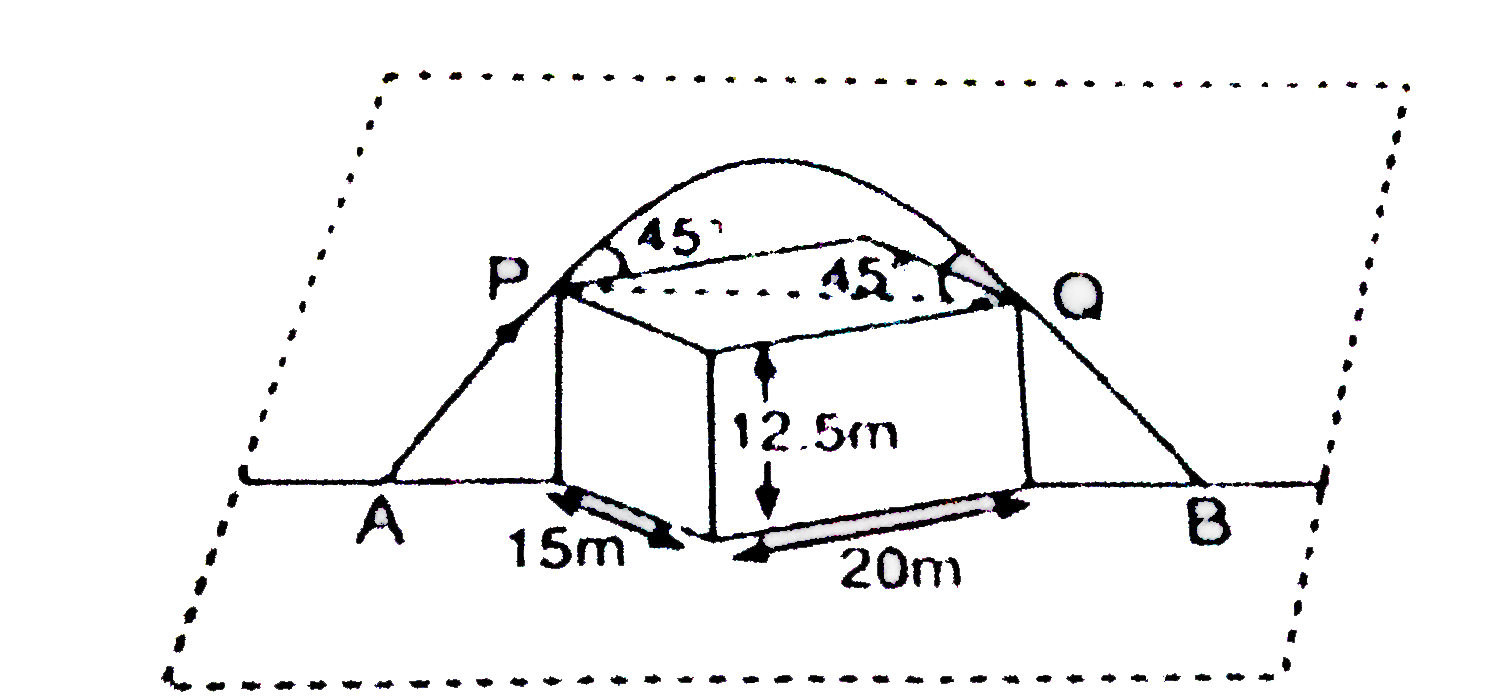
The speed of projection of the particle at A will be:View SolutionA particle is fired from 'A' in the diagonal plane of a building of dimension 20m (length)×15m (breath) xx12.5m (height), just clears the roof diagonally and falls on the other side of the building at B. It is observed that the particle is travelling at an angle 45∘ with the horizonal when it clears the edges P and Q of the diagonal. Take g=10m/s2.
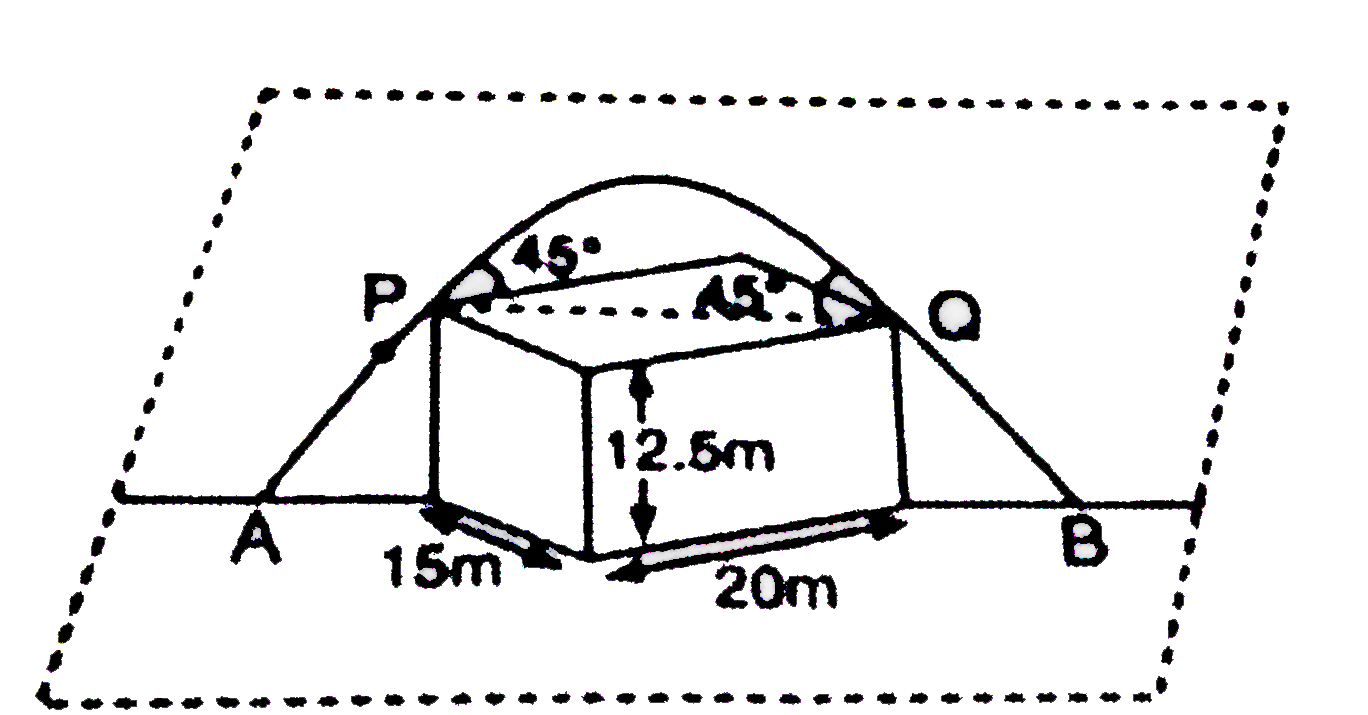
The range that is AB will be:View SolutionA particle is fired from 'A' in the diagonal plane of building of dimension 20 m (length)x 1.5 m (breadth) x 12.5 m (height) , just clears the roof diagonally & falls on the other side of the building at B. it is observed that the particle is travelling at an angle 45∘ with the horizontal whtn it clears tha edges P and Q of the diagonal Take g=10m/s2

The angle pf projection at A will be :View SolutionA particle is projected at an angle 60∘ with the horizontal with a speed 10m/s. Then, latus rectum is (Take g=10m/s2)
 View Solution
View Solution

