A commander fires a shell at certain angle of projection from A which clears the building of dimensions 20×15×12.5m in it's diagonal plane. Shell just clears the roof diagonally at points P and Q and falls on the other side of the building at B and makes angle 45∘ with the horizontal at P and Q as shown in the figure. If the range AB of the shell is a2×√b then find b? (a and b lowest possible integers)

The correct Answer is:3
PQ=√152+202=25
25=V2Psin(2×45∘)g⇒VP=5√10m/s
v2Asin2θ−2×10×12.5=(5√5)2
⇒VAsinθ=5√15m/s
VAcosθ=VPcos45∘=5√5m/sandθ=60∘
AB=VA2sin2θg=25√3
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physic48videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS18videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - Part-1 Physics15videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS45videos
TEST PAPER 4
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle is fired from A in the diagonal plane of a building of dimension 20m(length) × 15m (breadth) × 12.5m(height), just clears the roof diagonally & falls on the other side of the building at B.It is observed that the particle is travelling at an angle 45∘ with the horizontal when it clears the edges P and Q of the diagonal. Take g=10m/s2.
The range that is AB will be:
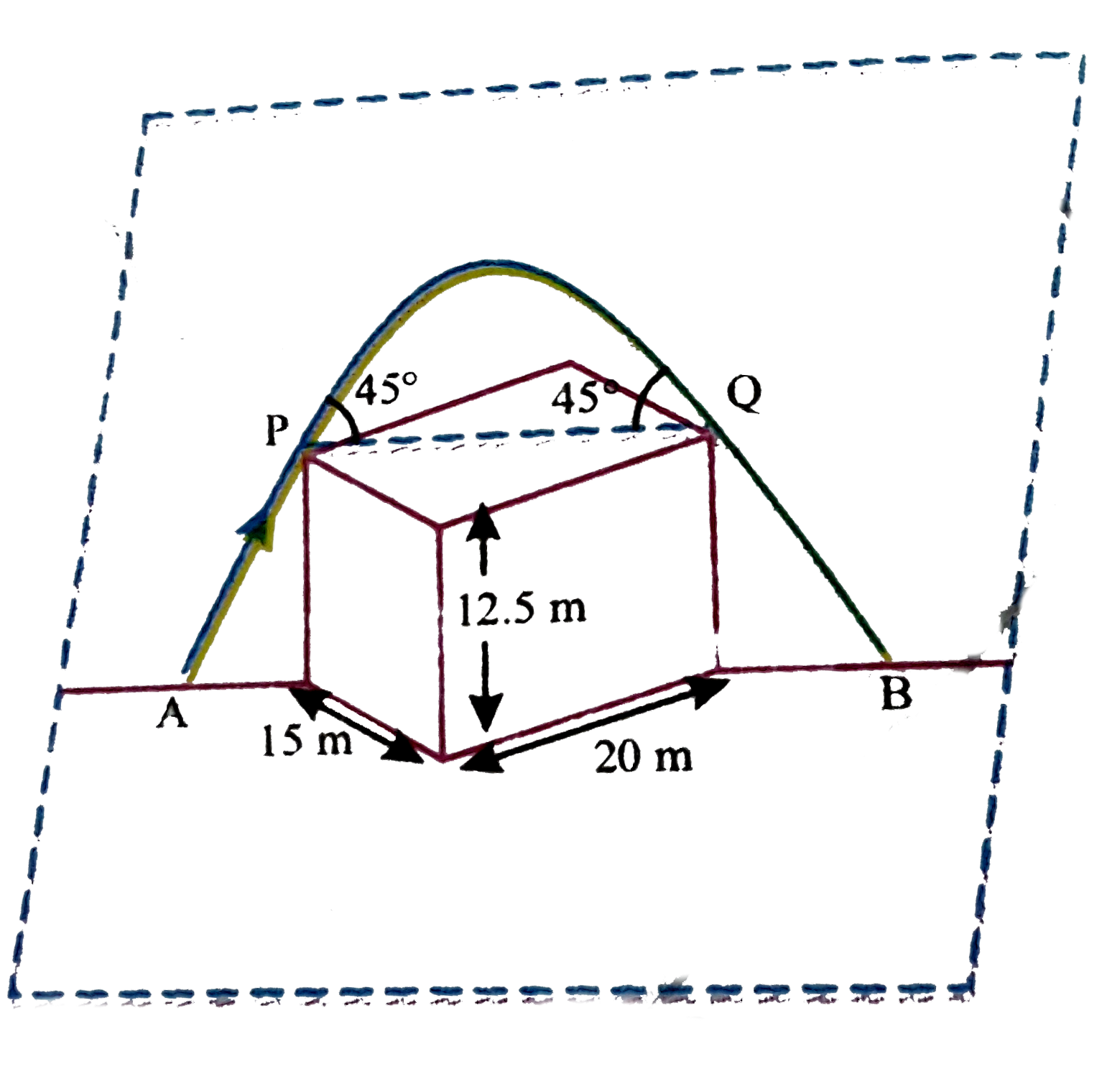 A5√10mB25√3mC5√15mD25√5m
A5√10mB25√3mC5√15mD25√5m - Question 2 - Select One
A particle is fired from 'A' in the diagonal plane of a building of dimension 20m (length)×15m (breath) xx12.5m (height), just clears the roof diagonally and falls on the other side of the building at B. It is observed that the particle is travelling at an angle 45∘ with the horizonal when it clears the edges P and Q of the diagonal. Take g=10m/s2.
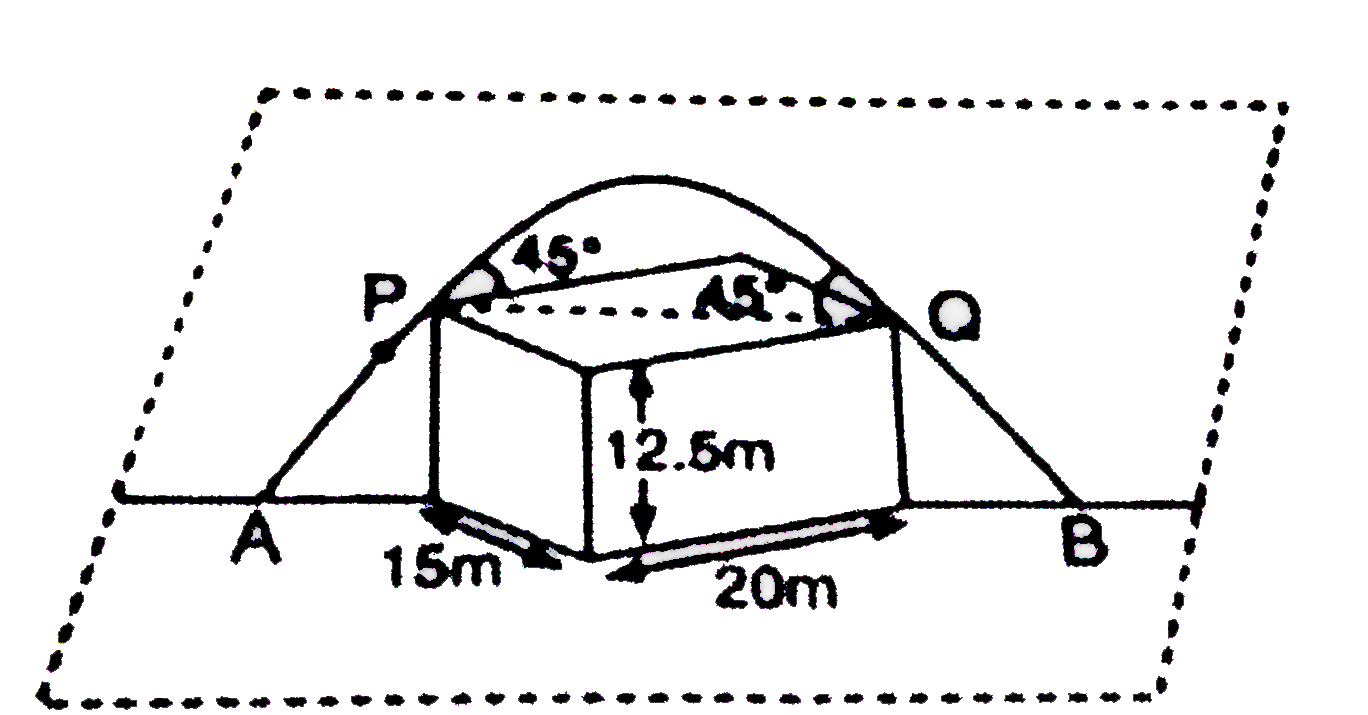
The range that is AB will be:A5√10mB25√3mC5√15mD25√5m - Question 3 - Select One
A particle is fired from 'A' in the diagonal plane of a building of dimension 20m (length)×15m (breath) xx12.5m (height), just clears the roof diagonally and falls on the other side of the building at B. It is observed that the particle is travelling at an angle 45∘ with the horizonal when it clears the edges P and Q of the diagonal. Take g=10m/s2.

The speed of the particle at point P will be:A5√10m/sB10√5m/sC5√15m/sD5√5m/s
A particle is fired from A in the diagonal plane of a building of dimension 20m(length) × 15m (breadth) × 12.5m(height), just clears the roof diagonally & falls on the other side of the building at B.It is observed that the particle is travelling at an angle 45∘ with the horizontal when it clears the edges P and Q of the diagonal. Take g=10m/s2.
The speed of the particle at point P will be:
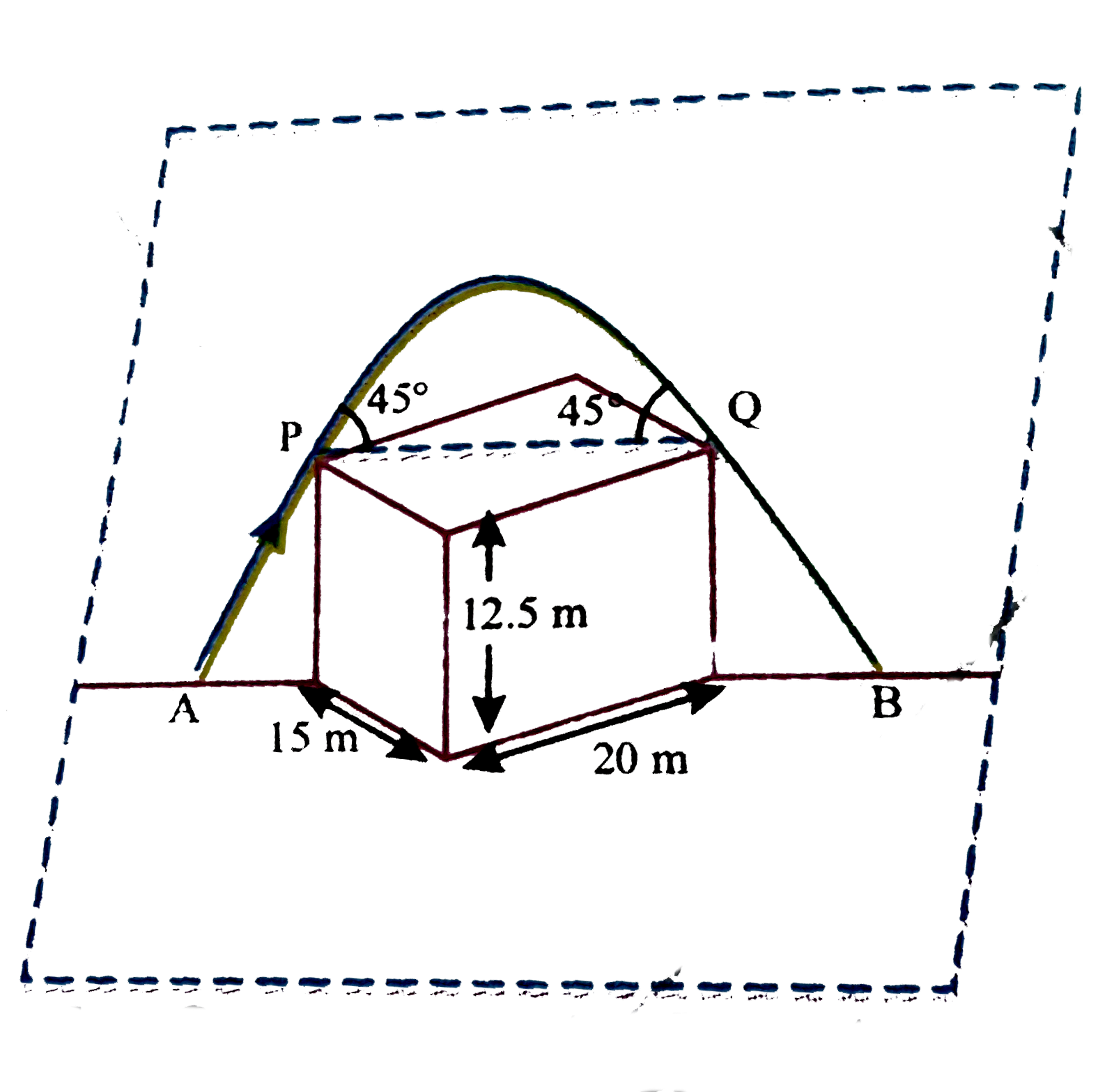 View Solution
View SolutionA particle is fired from A in the diagonal plane of a building of dimension 20m(length) × 15m (breadth) × 12.5m(height), just clears the roof diagonally & falls on the other side of the building at B.It is observed that the particle is travelling at an angle 45∘ with the horizontal when it clears the edges P and Q of the diagonal. Take g=10m/s2.
The speed of projection of the particle at A will be:
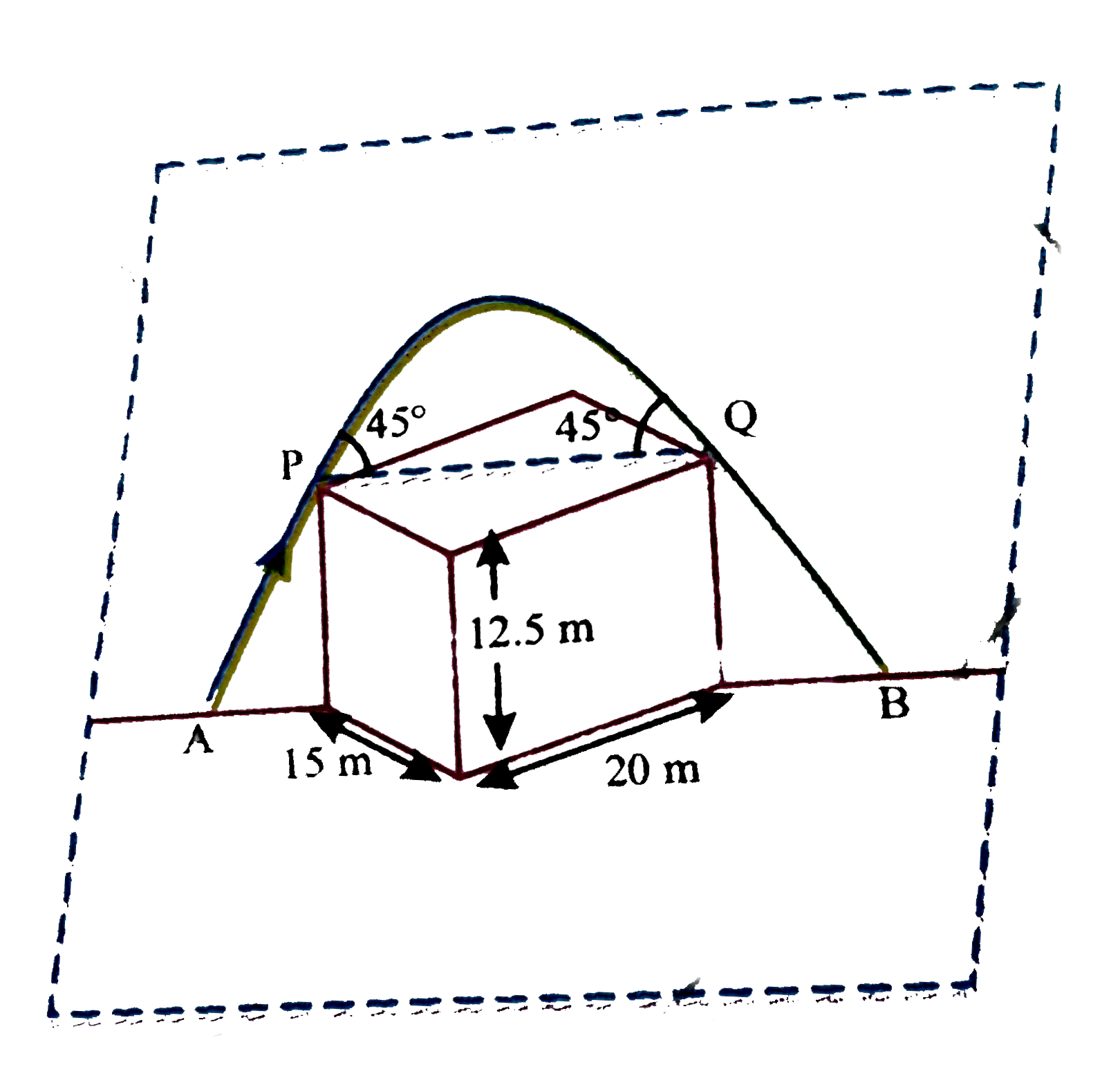 View Solution
View SolutionA particle is fired from 'A' in the diagonal plane of a building of dimension 20m (length)×15m (breath) xx12.5m (height), just clears the roof diagonally and falls on the other side of the building at B. It is observed that the particle is travelling at an angle 45∘ with the horizonal when it clears the edges P and Q of the diagonal. Take g=10m/s2.
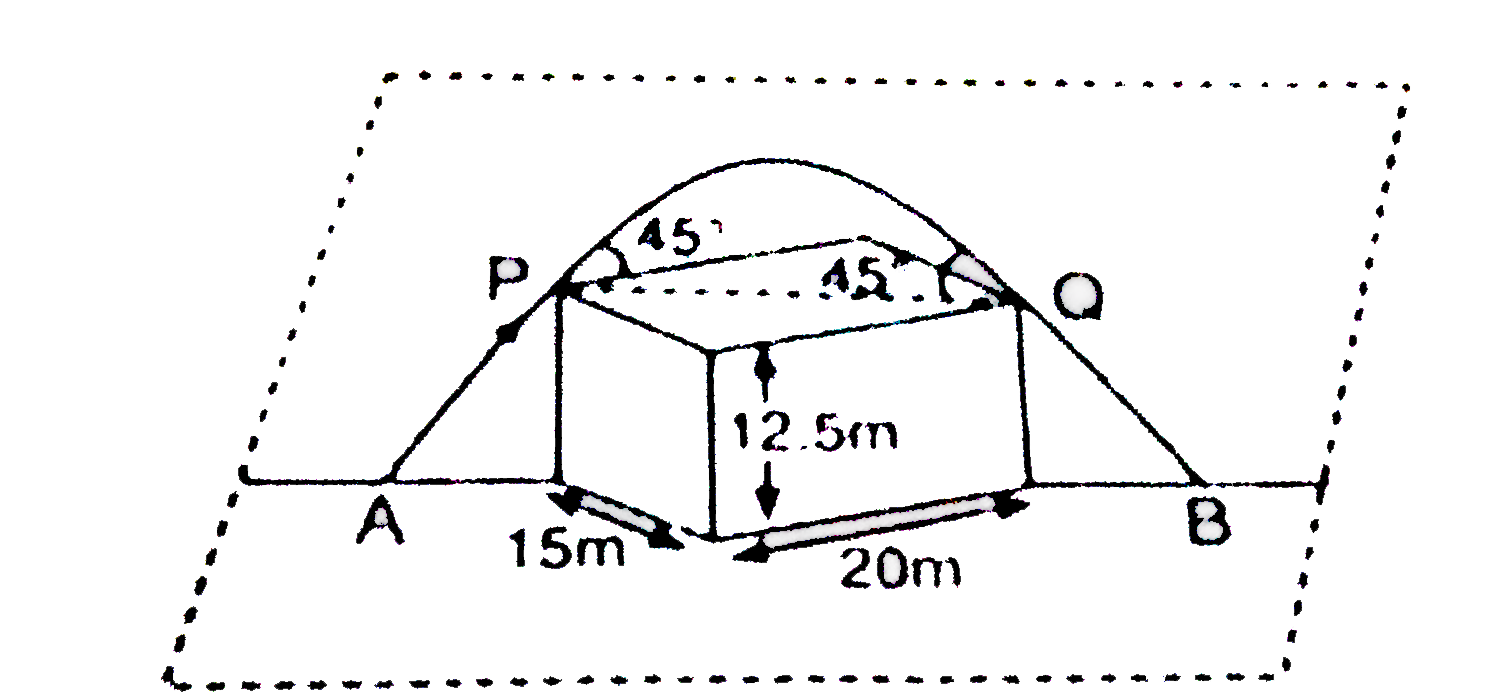
The speed of projection of the particle at A will be:View SolutionA particle is fired from 'A' in the diagonal plane of building of dimension 20 m (length)x 1.5 m (breadth) x 12.5 m (height) , just clears the roof diagonally & falls on the other side of the building at B. it is observed that the particle is travelling at an angle 45∘ with the horizontal whtn it clears tha edges P and Q of the diagonal Take g=10m/s2

The angle pf projection at A will be :View SolutionA projectile is fired at an angle of 45∘ with the horizontal. Elevation angle of the projection at its highest point as seen from the point of projection is
View Solution

