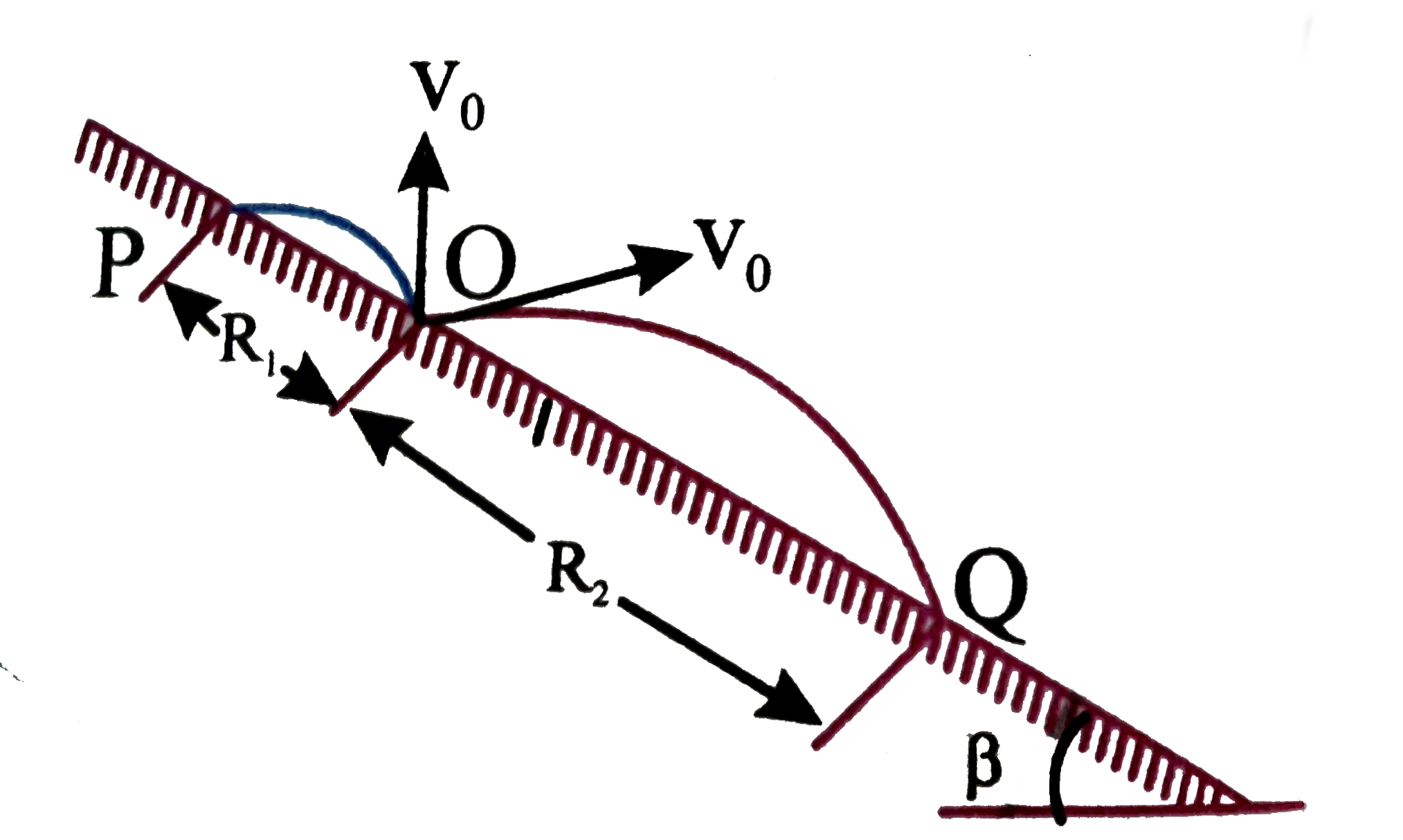
A body has maximum range R1 when projected up the plane. The same body when projected down the inclined plane, it has maximum range R2. Find the maximum horizontal range. Assume equal speed of projection in each case and the body is projected onto the inclined plane in the line of the greatest slope.
R=2R1R2R1−R2
R=2R1R2R1+R2
R=R1R2R1−R2
R=4R1R2R1+R2
The correct Answer is:B
As derive earlier, for upward projection, Rmax=v20g(1−sinβ)=R1…(i)
For downward projection,
Rmin=v20g(1−sinβ)=R2…(ii)
For a projection of horizontal surface substituting β=0,Then, we have Rmax=v20g(1−sinβ)=R(say)…(iii)
To establish a relation between R,R1 and R2 , we need to eliminate sinβ.Adding 1R1 form eq. (i) with 1R2 from eq.(ii) we have 2R=1R1+1R2 then, ans . R=2R1R2R1+R2
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-Vi multiple answer
16 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-VI Passage answer
18 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Integer
6 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)
24 Videos
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W
29 Videos
Similar Questions
Knowledge Check
A body has maximum range R1 when projected up the inclined plane. The same body when projected down, the inclined plane. It has maximum range R2. Find its maximum horizontal range. Assume the equal speed of projection in each case and the body is projected onto the gretest slope.
 AR=2R1R2R1−R2BR=2R1R2R1+R2CR=R1R2R1−R2DR=4R1R2R1+R2
AR=2R1R2R1−R2BR=2R1R2R1+R2CR=R1R2R1−R2DR=4R1R2R1+R2If R is the range of a projectiel on a horizontal plane and h its maximum height, the maximum horizontal range with the same velocity of projection is:
A2hBR28hC2R+h28RD2h+R28hThe horizontal range and the maximum height of a projectile are equal. The angle of projection of the projectile is
Aθ=tan−1(14)Bθ=tan−1(4)Cθ=tan−1(2)Dθ=45∘
A projectile when fired at a certain inclination has maximum rang R. Find its maximum height attained by it in terms of R .
View SolutionFor a projectile projected at an angle _____the maximum height and horizontal range are equal.
View SolutionFor a given velocity of projection from a point on the inclined plane, the maximum range down the plane is three times the maximum range up the incline. Then find the angle of inclination of the inclined plane.
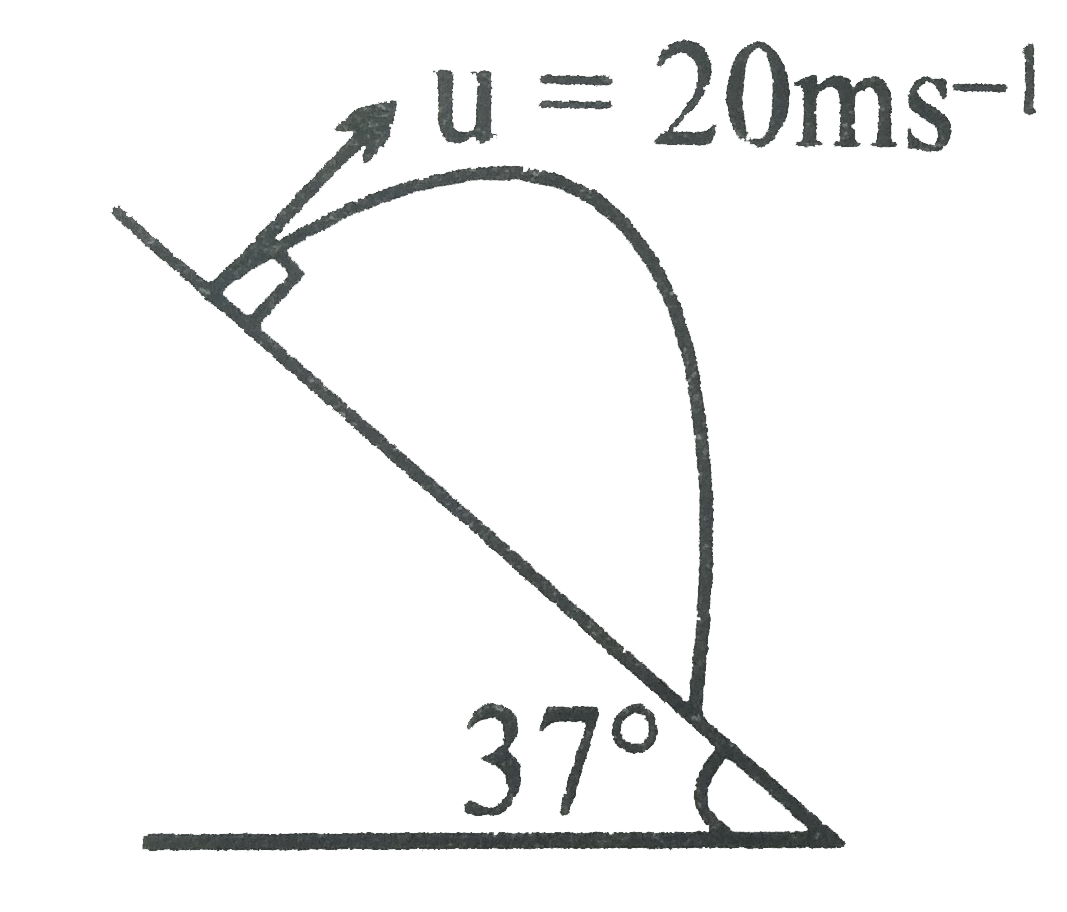
View SolutionFind range of projectile on the inclined plane which is projected perpendicular to the incline plane with velcoity 20m/s as shwon in figure.
View SolutionA body is projected with velocity u so that its horizontal range is twice the maximum height.The range is
View Solution
