Two particles are projected from the same point on ground simultaneously with speeds and 20m/sand20/√3 at angles 30∘ and 60∘ with the horizontal in the same direction.The maximum distance between them till both of them strike the ground is approximately (g=10m/s2)
23.1m
16.4m
30.2m
10.4m
The correct Answer is:A
Components of velocities of both the particles in vertical direction are equal.Therefore, their time of flights are equal and their relative motion is in horizontal direction only.Thus, the maximum distance between them is equal to the difference in their horizontal ranges.
R1(20)2sin60∘g=(400)√310×2=34.64m
R2=(20√3)2sin120∘g=400×√310×3×2=11.55m
∴Smax=34.64−11.55=2309m=23.1m
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-Vi multiple answer16videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-VI Passage answer18videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Integer6videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)24videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W29videos
MOTION IN A STRAIGHT LINE
Similar Questions
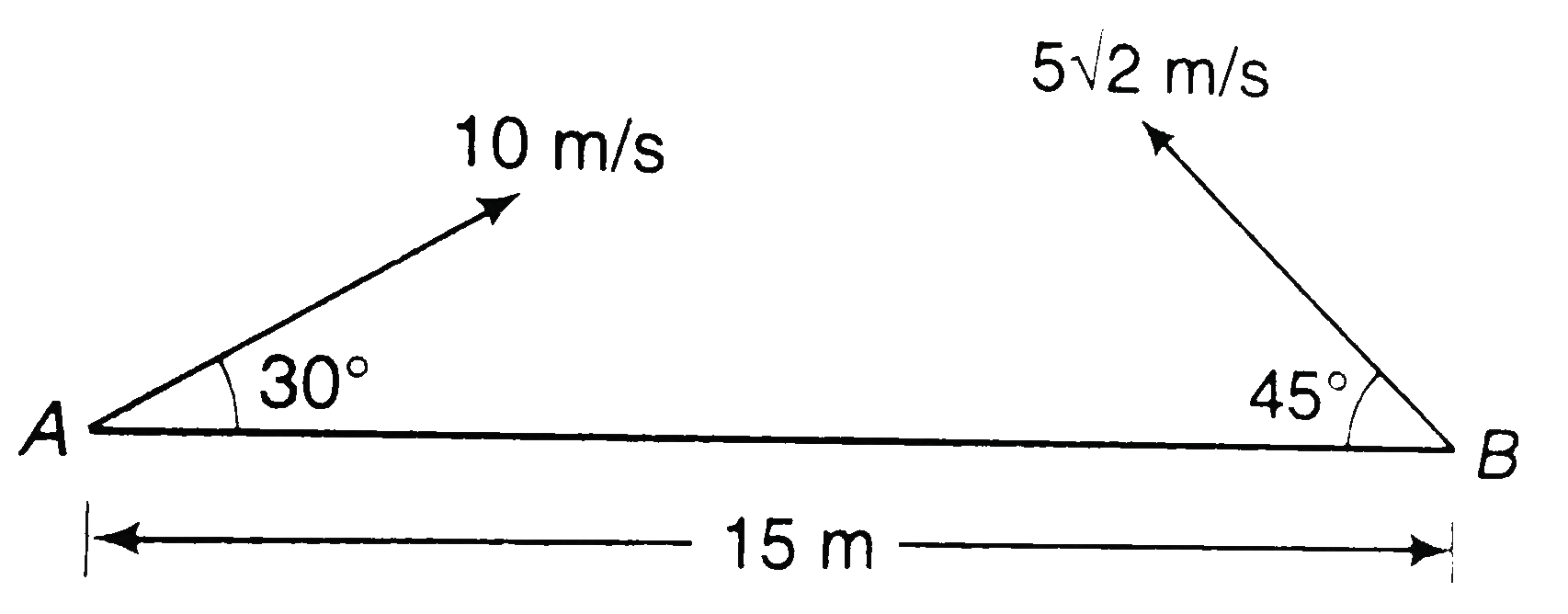
Two particles A and B are projected from ground towards each other with speeds 10m/s and 5(√2)m/s at the angle 30∘and45∘ with horizontal from two points separated by a distance of 15 m.
will they collide or not ?
 View Solution
View SolutionA particle is projected from the ground with an initial velocity of 20m/s at angle fo 30∘ with the horizontal. What is the magnitude of chang in velocity in 0.5scond ? ( g= 10 m//s^2).
View Solution
Knowledge Check
- Question 1 - Select One
Two particle are projected from the same point on ground simultaneously with speed 20m/s and 20/√3m/s at angle 30∘ and 60∘ with the horizontal in the same direction. The maximum distance between them till both of them strikes the ground is approximately (g=10m/s2)
A23.1mB16.4mC30.2mD10.4m - Question 2 - Select One
Two particles are projected from two points 4m apart on the horizontal ground, simultaneously with speed 20ms−1 above 60∘ and 15ms−1 above 30∘ from horizontal towards each other. Find the shortest distance between them during the flight.
A3.9mB2.8mC1.7mD1.5m - Question 3 - Select One or More
A particle is projected at an angle θ from ground with speed u (g = 10 m/s2 )
Aif u = 10 m/s and θ=30∘, then time of flight will be 1 secBIf u=10√3m/sandθ=60∘, then time of flight will be 3 sec.Cif u=10√3m/sandθ=60∘, then after 2 sec velocity becomes perpendicular to initial velocity.Dif u = 10 m/s and θ=30∘, then velocity never becomes perpendicular to initial velocity during its flight.
Two particles of equal mass are projected simultaneously with speeds 20m/s end 10√3m/s as shown in figure. Find the maximum height reached by the centre of mass of the particles
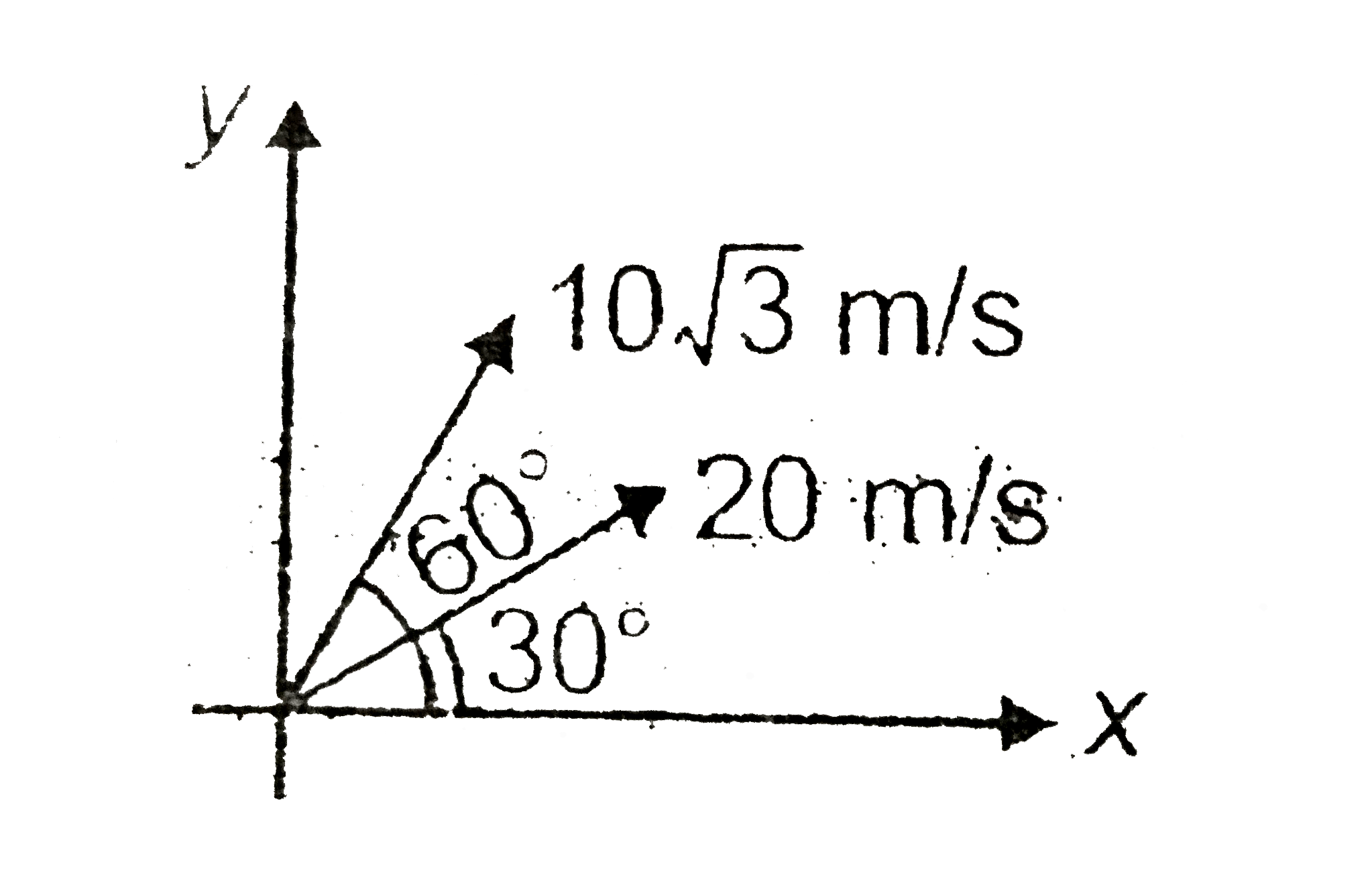 View Solution
View SolutionA particle is projected with a speed of "18m/s" at an angle of 60∘ with the horizontal.The average velocity of the particle between two instants when it is at the same height is
View SolutionTwo particles P & Q are projected simultaneously from a point O on a level ground in the same vertical plane with the same speed in directions making angle of 30∘ and 60∘ respectively with the horizontal.
View SolutionTwo particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then :
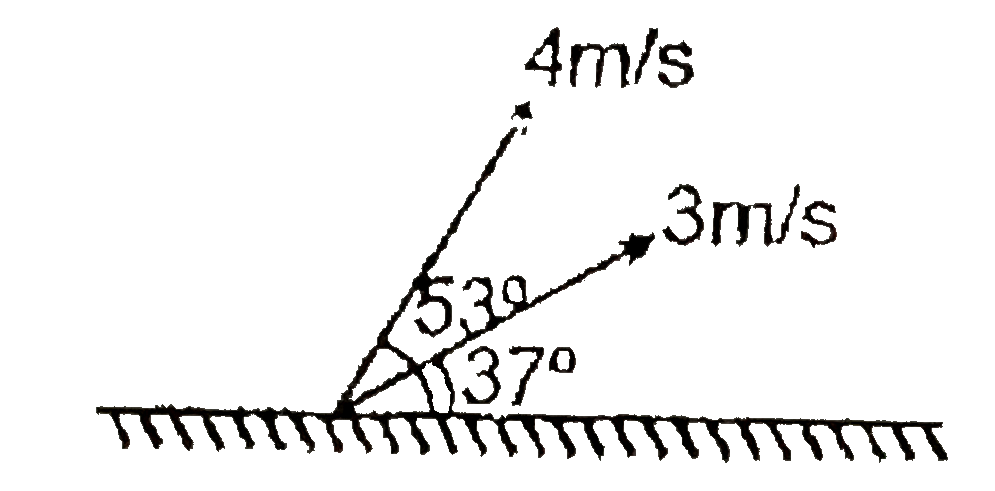 View Solution
View SolutionTwo particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then:
 View Solution
View Solution

