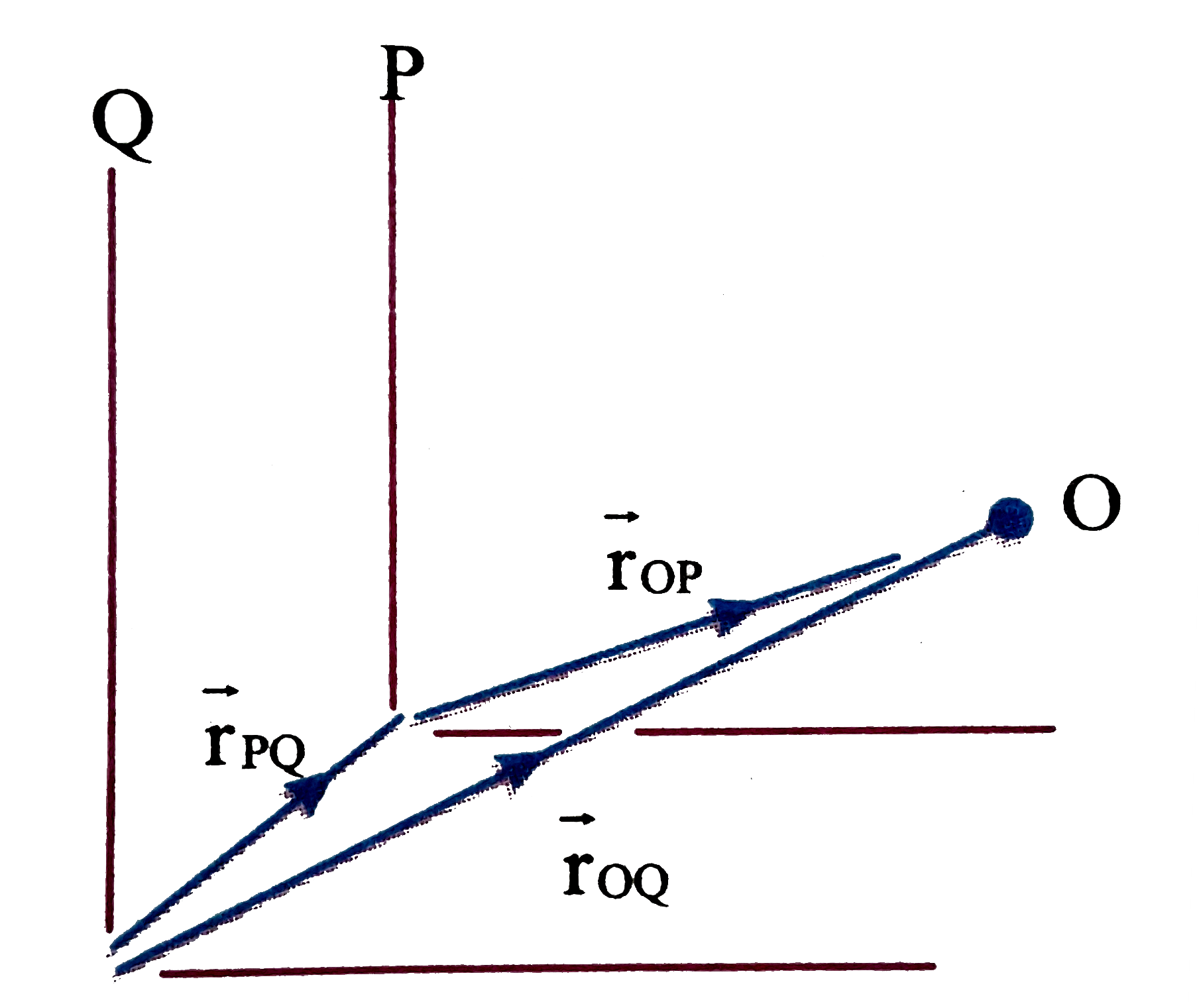
Two frames of reference P and Q are moving relative to each other at constant velocity. Let →vOP and →aOP represent the velocity and the acceleration respectively of a moving particle O as measured by an observer in frame P and →VOQ and →aOQ represent the velocity and the acceleration respectively of the moving particle O as measured by an observer in frame Q, then
→vOP=→vOQ
→vOP=→vOQ+→vQP
→aOP=→aOQ
→aOP=→aOQ+→aQP
The correct Answer is:B, C, D
¯rOQ=¯rPR+¯rOP,¯rOQ=¯rPQ+¯rOP,¯rOQ=¯aOQ=¯¯¯O+¯aOP
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-VI Passage answer18videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-Vi Integer9videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-Vi single answer30videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)24videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W29videos
MOTION IN A STRAIGHT LINE
Similar Questions
The position, velocity and acceleration of a particle moving with a constant acceleration can be represented by :
View SolutionThe velocities of two particles of masses m1 and m2 relative to an observer in an inertial frame are v1 and v2. Determine the velocity of the center of mass relative to the observer and the velocity of each particle relative to the center of mass.
View Solution
Knowledge Check
- Question 1 - Select One
Let v and a represent instantaneous velocity and acceleration of a particle respectively.
AAcceleration a can be zero when velocity v =cancel0BAcceleration a can be nonzero when velocity v=0CAcceleration a can be zero when velocity v=0DAcceleration a must be zero when velocity v=0. - Question 2 - Select One
For a particle moving in a straight line assume s,v,a and t represents displacement, velocity, acceleration and time respectively.
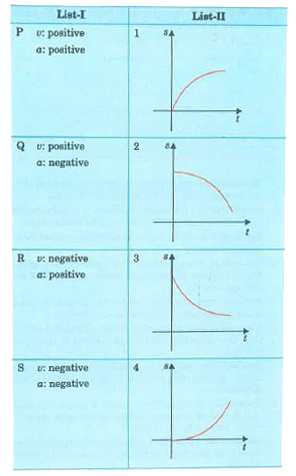 APQRS3241BPQRS1324CPQRS2134DPQRS4132
APQRS3241BPQRS1324CPQRS2134DPQRS4132 - Question 3 - Select One
Two identical particles move towards each other with velocity 2v and v, respectively. The velocity of the centre of mass is:
AvBv/3Cv/2Dzero
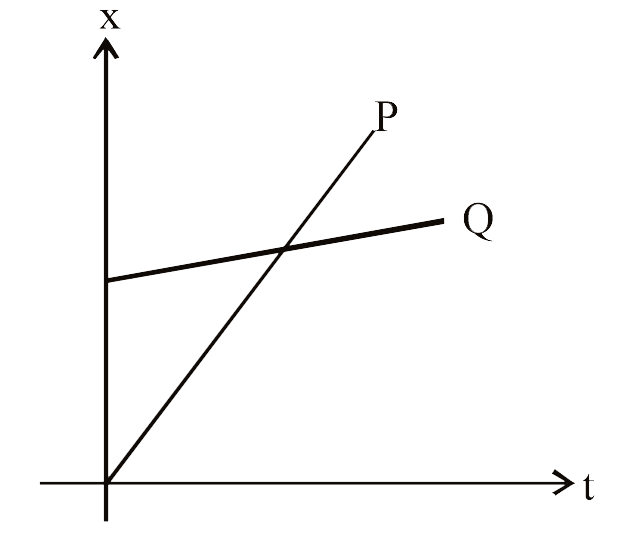
Two bodies P and Q are moving along positive x-axis their position-time graph is shown below. If →VPQ is velocity of
 View Solution
View SolutionThe velocity components of a particle moving in the xy plane of the reference frame K are equal to vx and vy. Find the velocity v′ of this particle in the frame K in the positive direction of its x axis.
View SolutionTwo identical particles move towards each other with velocity 2v and v respectively. The velocity of centre of mass is
View SolutionSuppose that two objects A and B are moving with velocities →vA and →vB (each with respect to some common frame of refrence). Let →vAB represent the velocity of A with respect to B. Then
View SolutionVelocity and acceleration vector of a charged particle moving in a magnetic field at some instant are →v=3ˆi+4ˆjand→a=2ˆi+xˆj. Select the correct options.
View Solution

