If two chords AB and AC of a circle with centre O are such that the centre O lies on the bisector of ∠BAC; Prove that AB=AC
Step by step video & image solution for If two chords AB and AC of a circle with centre O are such that the centre O lies on the bisector of /_BAC; Prove that AB=AC by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Two chords AB and CD of a circle with centre O intersect at point P within the circle. ∠AOC+∠BOD=?
A∠APCB2∠APCC32∠APCDNone of theseA,B and C are three points on a circle such that the angles subtended by the chords AB and AC at the centre O are 90∘ and 110∘ respectively . Further suppose that the centre O lies on the interior ∠BAC. The ∠BAC is
A40∘B80∘C160∘D20∘AB and AC are tangents to the circle with centre O. Then x equals.
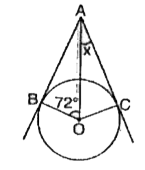A22∘B18∘C20∘D36∘
Two chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the angle bisector of ∠BAC.
View SolutionTwo chords AB and AC of a circle with centre O are on the opposite sides of OA. Then, ∠OAB=∠OAC.
View SolutionIn the given figure, AB and AC are two equal chords of a circle with centre O. Show that O lies on the bisectors of ∠BAC.
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionIn a circle with centre O, chords AB and CD intersect inside the circumference at E. Prove that ∠AOC+ ∠BOD=2 ∠AEC
View Solution