Question

Pythagorous Theorem and Important results

Explanation

Pythagoras Theorem

In this chapter, we will discuss Pythagoras Theorem. Well, this is a very important topic in Maths which needs clear understanding. This theorem explains the relations between the sides of a right-angled triangle. Students should keep in mind that this is also known as Pythagorean Theorem.

Here, in this chapter, students would be able to understand the formula and proof of the theorem. By using this theorem, we can understand how to find the length of the base, perpendicular and hypotenuse formula of a right-angled triangle. So, let us go ahead and understand it in the best way.

Pythagoras Theorem Statement

According to the Pythagoras theorem, “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.” In this case, the sides of the triangle have been termed as Base, Perpendicular and Hypotenuse.  Here, the longest side is the hypotenuse because of the reason that it is opposite to the 90⁰ angle. If we take the sides of a right triangle as a, b and c, having the values of a positive integer, it is known as a Pythagorean triple. This is seen when the sides of a right triangle are squared and put into an equation.

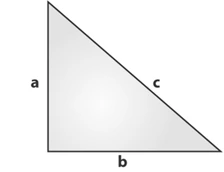
Pythagoras Theorem Formula

Look at the triangle above.

You can see that

Perpendicular side = a

Base = b

Hypotenuse side = c

When we make use of the Pythagoras Theorem Formula,

i.e, Hypotenuse² = Perpendicular² + Base²

So, we get c² = a² + b²

Students should remember that the side which is opposite to the 90⁰ (right angle) is the longest side. This is also known as hypotenuse because the side opposite to the greatest angle is the longest.

In the above figure, we find a, b and c are mounted on the three sides of a triangle. Well, it has the same sides as shown.

According to the Pythagoras Theorem,

Area of square A + Area of square B = Area of square C

Related Videos:

• Similar Triangles and their properties


• Similar Polygons


• State and prove the Pythagoras theorem


• How similarity is different from congruence

Pythagoras Theorem Proof

Here, it is given: A right-angled triangle ABC.

You have to prove that AC² = AB² + BC²

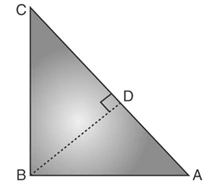
Proof:  We need to draw a perpendicular line BD onto the side AC

We know, △ADB ~ △ABC

Therefore, ADAB=ABAC (Condition for similarity)

Or, AB² = AD × AC ……………………………..……..(1)

Also, △BDC ~△ABC

Therefore, CDBC=BCAC (Condition for similarity)

Or, BC²= CD × AC ……………………………………..(2)

Now adding (1) and (2) we get,

AB² + BC² = AD × AC + CD × AC

AB² + BC² = AC (AD + CD)

Since, AD + CD = AC

Therefore, AC² = AB² + BC²

Hence, the Pythagorean theorem is proved.

Important note: It is only to the Right Angled Triangle that Pythagoras Theorem is applicable.

Applications of Pythagoras Theorem

• To get the right idea whether the triangle is a right-angled triangle or not.


• To  calculate the diagonal of a square


• If two sides of a right-angled are given, then it is possible to calculate the length of any side.

Pythagorean Theorem Problems

Problem 1: The sides of a triangle are 7, 9 & 12 units. Find out whether it is a right angle or not.

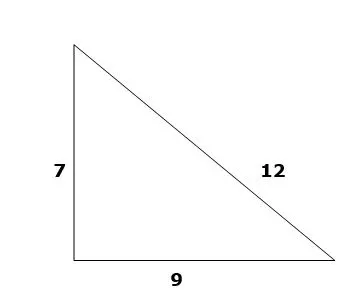
Solution: From Pythagoras Theorem, we have;

Perpendicular² + Base² = Hypotenuse²

Perpendicular = 7 units

Base = 9 units

Hypotenuse = 12 units

7² + 9² = 12²

⇒ 49 + 81 = 144

⇒ 130 = 144 

L.H.S. = R.H.S.

Therefore, the angles opposite to the 12 unit side cannot be a right angle.

Problem 2

In the figure below, the two sides of a right-angled have been shown. Can you find out the third side?

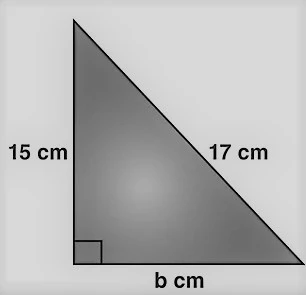
Solution: Given;

Perpendicular = 15 cm

Base = b cm

Hypotenuse = 17 cm

As per the Pythagorean Theorem, we have;

Perpendicular² + Base² = Hypotenuse²

⇒ 15² + b² = 17²

⇒ 225 + b² = 289

⇒ b² = 289 – 225

⇒ b² = 64

⇒ b = √64

Therefore, b = 8

Problem 3: In the figure below, the sides of a square are 4 cm. Can you find the length of the diagonal?

Solution- Given;

Sides of a square = 4 cm

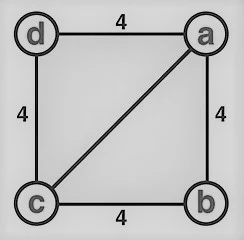
What To Find - The length of diagonal ac.

Let us consider triangle abc or acd

(ab)² + (bc)² = (ac)²

(4)² + (4)² = (ac)²

16 + 16 = (ac)²

32 = (ac)²

(ac)²  = 32

or ac = 4√2.

Therefore, the length of the diagonal is 4√2.

Problem 4: In the below figure, you can find the two sides of 3 cm and 4 cm. Find out the length of the hypotenuse.

                            

Solution: Let the length of the hypotenuse = c

Here, a =3 and b = 4

Now, we apply the formula, which is:

   a² + b² = c²

  ⇒ 3² + 4² = c²

   ⇒ 9 + 16 = c²

   ⇒ 25 = c²

     ⇒ √25 = c²

     ⇒ 5 = c

Now, we will check this answer to verify:

3² + 4² = 5²

⇒ 9 + 16 = 25

⇒ 25 = 25

Therefore, we can conclude that the length of the hypotenuse is 5.

Important Chapters:

• NCERT Solution for Maths


• NCERT Solution for Maths Class 7 Chapter The Triangles and its Properties


• NCERT Solution for Maths Class 9 Chapter Triangles


• NCERT Solution for Maths Class 10 Chapter Triangles