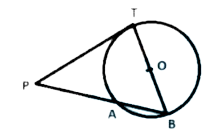
If PAB are secant to the circle and PT is tangent segment; then PA×PB=PT2
Step by step video & image solution for If PAB are secant to the circle and PT is tangent segment; then PAxxPB=PT^2 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
In the given figure, TB is a chord which passes through the centre of the circle . PT is a tangent to the circle at the point T on the circle . If PT=10cm, PA=5cm and AB=xcm, then the radius of the circle is :
 A5√3cmB6√5cmC3√5cmD10√3cm
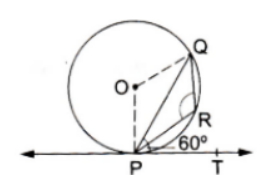
A5√3cmB6√5cmC3√5cmD10√3cmIn the figure , PQ is a chord of a circle and PT is a tangent at P such that ∠QPT=60∘, then ∠PRQ =
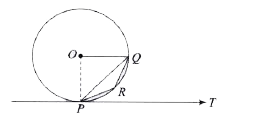 A100∘B110∘C120∘D150∘
A100∘B110∘C120∘D150∘In the figure, PT = 5 cm, PA = 4 cm. Find AB
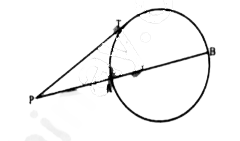 A49cmB94cmC5cmD23cm
A49cmB94cmC5cmD23cm
Let PAB be a secant to a circle intersecting the circle at A and B. Let PT be the tangent segment. If PA = 9 cm and PT =12 cm, then what is AB equal to?
View SolutionIn the given figure, TB is a chord which passes through the centre of the circle. PT is a tangent to the circle at the point T on the circle. If PT = 10 cm, PA = 5 cm and AB = x cm. then the radius of the circle is:
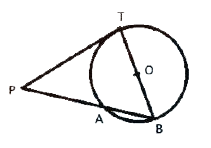
View SolutionAs shown in the figure, PA is a tangent to a circle and PBC is a secant, so that PB = AB. Prove that PB.PC=AC2
View SolutionIn the adjoining figure, PQ is a chord of a circle and PT is the tangent at P such that ∠QPT=60∘.Find ∠PRQ.
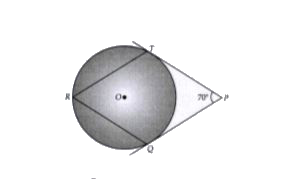
View SolutionIn figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ=70∘, find ∠TRQ.
View Solution
