As shown in the figure, PA is a tangent to a circle and PBC is a secant, so that PB = AB. Prove that PB.PC=AC2
As PA is tangent to circle and PBC is a secant. So, from secant rule:
PA2=PB⋅PC eq(1)
As, PA is tangent to AC,
∠ACB=∠PABeq(2)
Given that PB=AB, So,
∠PAB=∠APBeq(3)
From eq(2) and eq(3),
∠ACB=∠APB
So, PA = AC, putting this in eq(1)
AC2=PB⋅PC
Similar Questions
In the figure, AB is a diameter PA is a tangent to the circle and PCB is a secant. Show that △ABP~△CAP
View SolutionIn the following figure, ray PA is the tangent to the circle at point A and PBC is a secant. If AP = 14, BP = 10, then find BC.
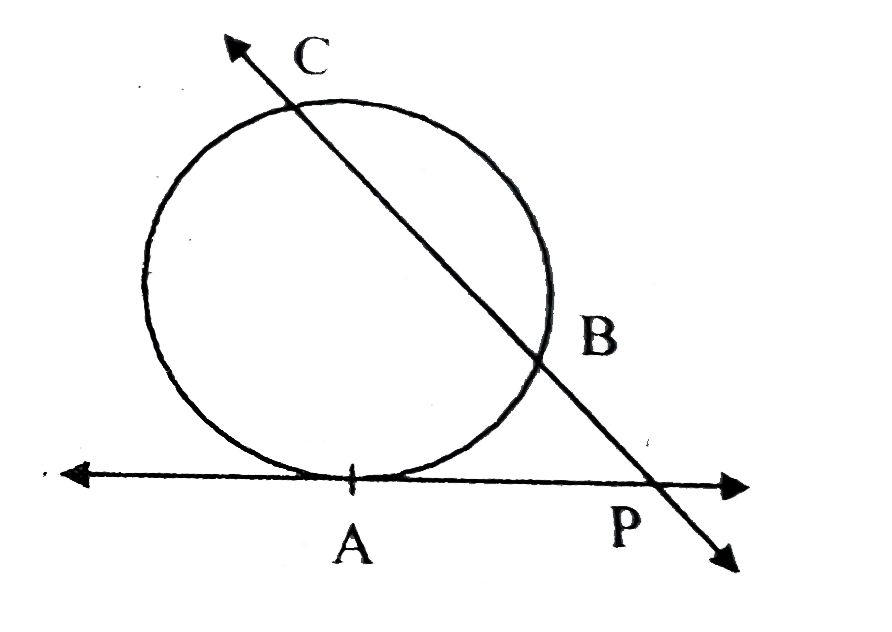
View SolutionIn the following figure , ray PA is the tangent to the circle at point A and PBS is secant . If AP=14,BP=10, find BC.
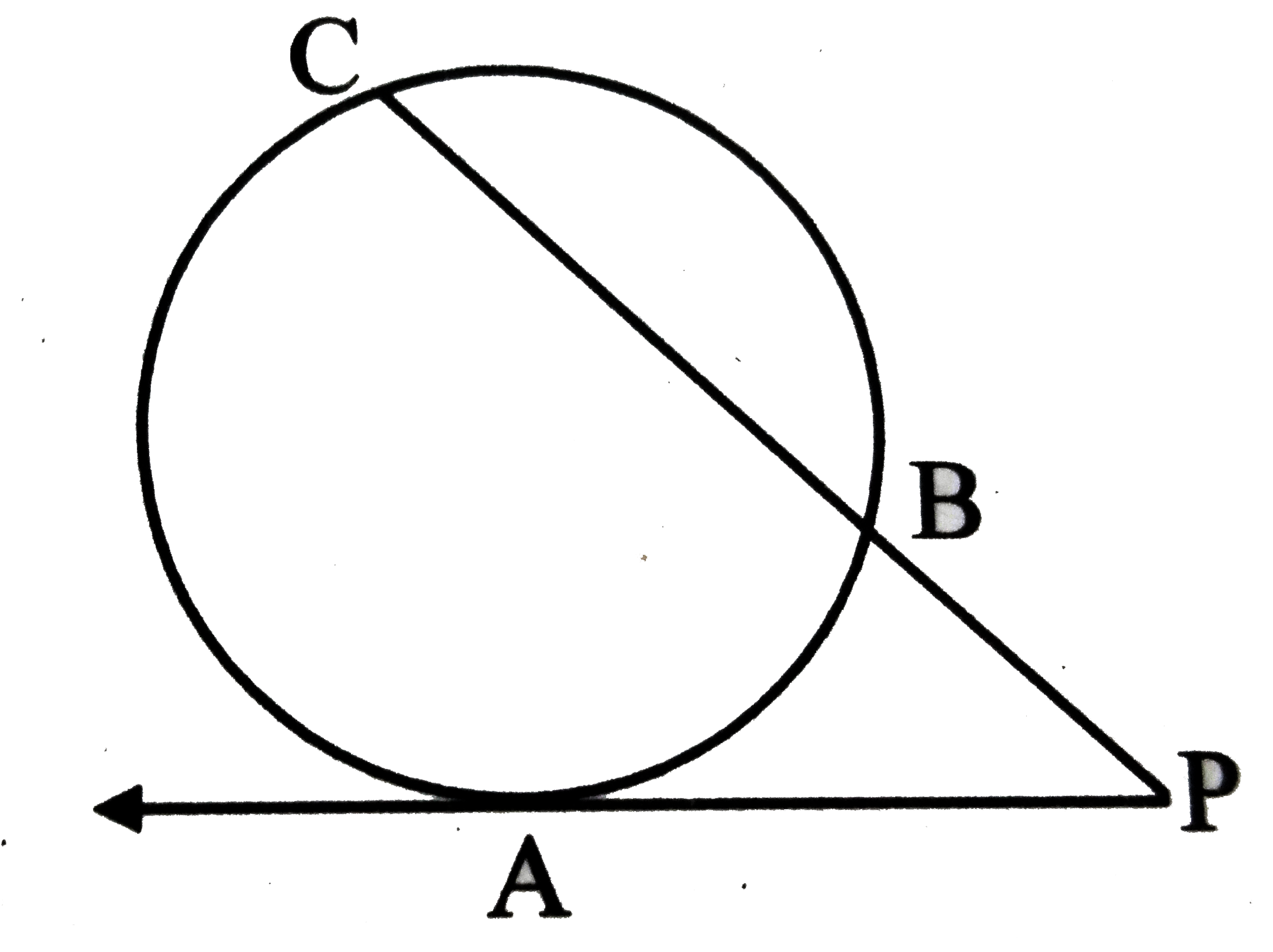
View SolutionIf PAB are secant to the circle and PT is tangent segment; then PA×PB=PT2
View SolutionTwo tangent segments PA and PB are drawn to a circle with centre O such that ∠APB=120o . Prove that OP=2 AP .
View SolutionIn the given figure, a tangent segment PA touching a circle in A and a secant PBC are shown. If AP = 15 cm and BP = 10 cm, find the length of PC.

View SolutionIn the figure, a tangent PT and 2 line signs PBA is drawn to a circle with center O. If OL⊥AB. Prove that the PA×PB=PT2.
View SolutionIn the given Fig. 5, from an external point P, a tangent PT and a secant PAB is drawn to a circle with centre 0. ON is perpendicular on the chord AB. Prove that PA.PB=PT2?.

View SolutionAs shown in the given figure, from an external point P, a tangent PT and a line segment PAB are drawn to a circle with centre O. ON is perpendicular on the chord AB, Prove that
PA.PB=PN2−AN2
View SolutionIn the adjoining figure, AB>AC and the angle bisectors of ∠B and ∠C meet at point P. Prove that
PB>PC.

View Solution
