Let AB and CD be parallel chords of a circle with centre O; M is the mid point of AB and N is the mid point of CD. Prove that O,N,M are to lines.If MN = 3cm , AB = 4cm, CD = 10cm. find the radius of circle.
ON⊥CD
OM⊥AB
so, ONM are on same line.
In∠ONC
by pythagorus theoram
OC2=ON2+CN2
r2=x2+52
r2=x2+25
similarly, In ∠OAM
r2=x2−6x+13
From 1 and 2
x2+25=x2−6x+13
6x=12
x=2
From eq1
r2=x2+25
r2=19
r=±√29cm
Similar Questions
M and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that :
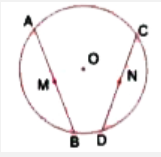
∠AMN=∠CNM.
View SolutionIn the given figure, AB and CD are two equal chords of a circle, with centre O. If P is the mid-point of chord AB, Q is the mid-point of chord CD and ∠POQ=150∘ find angleAPQ
View SolutionIn the given diagram 'O is the centre of the circle and AB is parallel to CD. AB = 24 cm and distance between he chord AB and CD is 17 cm. It the radius of the circle is 13 cm, find the length of the chord CD.
View SolutionIn the figure, M is the mid-point of [AB] and N is the mid-point of [CD] and O is the mid-point of [MN]. Prove that : vec(BC)+vec(AD)=2vec(MN) .
View SolutionABCDA is a quadrilateral of a circle ABCD of radius r and center at O. Here AB is the diameter, and CD is parallel to and half of AB. If the circle completes one rotation about the centre, then the locus of the mid-point of CD is a circle of what radius?
View SolutionL and M are mid-points of two eqal chords AB and CD of a circle with centre O Prove that angleOLM = angleOML
View SolutionL and M are mid-points of two equal chords AB and CD of a circle with centre O Prove that angleALM = angleCML
View SolutionEqual chords AB and CD of a circle with centre O, cut at right angles at E. If L and M are the mid-points of AB and CD respectively, prove that OLEM is a square.
View Solution
