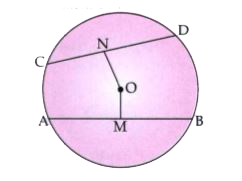
In the given diagram 'O is the centre of the circle and AB is parallel to CD. AB = 24 cm and distance between he chord AB and CD is 17 cm. It the radius of the circle is 13 cm, find the length of the chord CD.
The correct Answer is:10 cm
To solve the problem step-by-step, we will use the properties of circles, triangles, and the Pythagorean theorem.
Step 1: Understand the Given Information
- We have a circle with center O.
- Chord AB is parallel to chord CD.
- Length of chord AB (AB) = 24 cm.
- Distance between the chords AB and CD = 17 cm.
- Radius of the circle (OA) = 13 cm.
Step 2: Find the Half-Length of Chord AB
Since AB is a chord, we can find the midpoint M of AB. The length of AM will be half of AB.
AM=AB2=24 cm2=12 cm
Step 3: Apply the Pythagorean Theorem in Triangle OAM
In triangle OAM, we can apply the Pythagorean theorem:
OA2=AM2+OM2
Where:
- OA = radius = 13 cm
- AM = 12 cm
- OM is the perpendicular distance from O to chord AB.
Substituting the known values:
132=122+OM2
169=144+OM2
OM2=169−144=25
OM=√25=5 cm
Step 4: Find the Distance ON
We know the distance from chord AB to chord CD is 17 cm. Therefore, we can find ON:
ON=Distance between chords−OM
ON=17 cm−5 cm=12 cm
Step 5: Apply the Pythagorean Theorem in Triangle OCN
Now, we will apply the Pythagorean theorem in triangle OCN:
OC2=ON2+CN2
Where:
- OC = radius = 13 cm
- ON = 12 cm
- CN is the half-length of chord CD.
Substituting the known values:
132=122+CN2
169=144+CN2
CN2=169−144=25
CN=√25=5 cm
Step 6: Find the Length of Chord CD
Since CN is half of chord CD, we can find the full length of chord CD:
CD=2×CN=2×5 cm=10 cm
Final Answer
The length of chord CD is 10 cm.
---
- We have a circle with center O.
- Chord AB is parallel to chord CD.
- Length of chord AB (AB) = 24 cm.
- Distance between the chords AB and CD = 17 cm.
- Radius of the circle (OA) = 13 cm.
Since AB is a chord, we can find the midpoint M of AB. The length of AM will be half of AB.
AM=AB2=24 cm2=12 cm
In triangle OAM, we can apply the Pythagorean theorem:
OA2=AM2+OM2
Where:
- OA = radius = 13 cm
- AM = 12 cm
- OM is the perpendicular distance from O to chord AB.
132=122+OM2
169=144+OM2
OM2=169−144=25
OM=√25=5 cm
We know the distance from chord AB to chord CD is 17 cm. Therefore, we can find ON:
ON=Distance between chords−OM
ON=17 cm−5 cm=12 cm
Now, we will apply the Pythagorean theorem in triangle OCN:
OC2=ON2+CN2
Where:
- OC = radius = 13 cm
- ON = 12 cm
- CN is the half-length of chord CD.
132=122+CN2
169=144+CN2
CN2=169−144=25
CN=√25=5 cm
Since CN is half of chord CD, we can find the full length of chord CD:
CD=2×CN=2×5 cm=10 cm
The length of chord CD is 10 cm.
Topper's Solved these Questions
Similar Questions
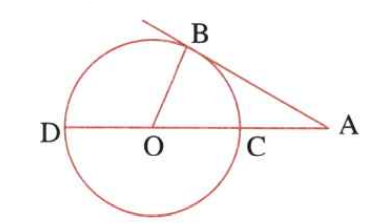
In the given figure, O is the centre of the circle ans AB is a tangent at B. If AB=15 cm and AC=7.5cm, calculate the radius of the circle.
View SolutionAB and CD are two chords such that AB = 10 cm , CD = 24 cm and AB // CD The distance between the chords is 17 cm . Find the radius of the circle.
View Solution
Knowledge Check
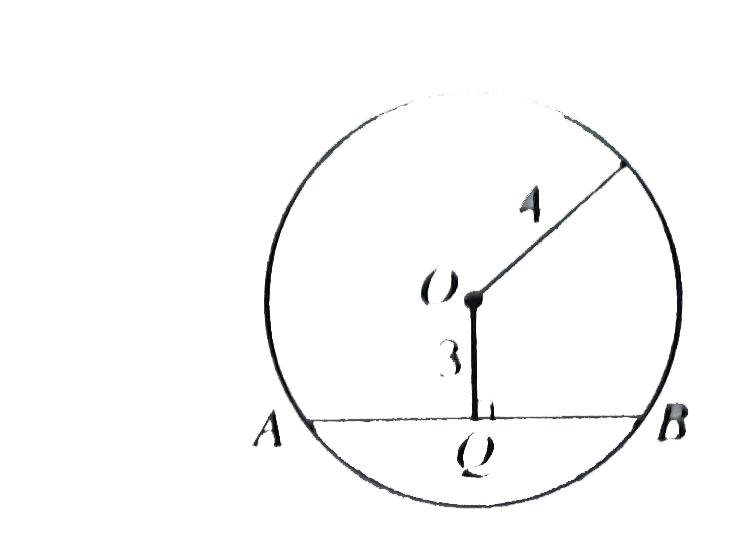
A chord ¯¯¯¯¯¯AB is 3 cm. from the center of a circle with radius 4. What is the length of chord ¯¯¯¯¯¯AB ?A√7B2√7C5D10
In the given figure O is the centre of the circle and AB is a tangents at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of the circle.
View SolutionIn the given 'O' is the centre of the circle, Arc AB=ArcBC=Cd.If∠OAB=48∘, find:
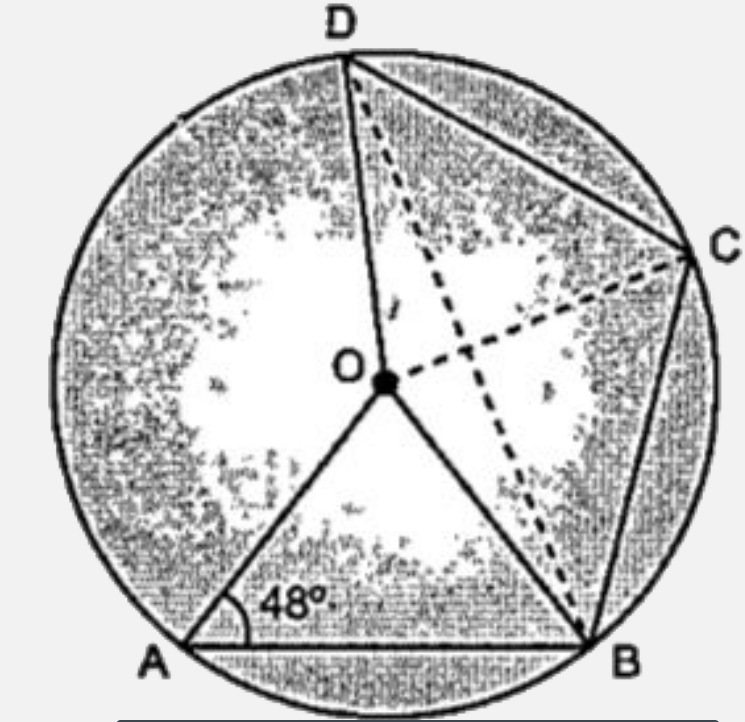
∠OBD
View SolutionLet ABCD be a trapezium ,in which AB is parallel to CD, AB =11 ,BC=4,CD=6 and DA=3. the distance between AB and CD is
View SolutionAB and CD are two parallel chords of a circle on opposite sides of a diameter such that AB = 24 cm and CD = 10 cm. If the radius of the circle is 13 cm, find the distance between the two chords.
View SolutionIn the adjoining figure O is the centre of the circle . If chord AB=2 cm radius OA=2 cm, then find the value of ∠ACB.

View SolutionIn the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the :
(i) radius of the circle
(ii) length of chord CD
View SolutionIn the adjoining figure, 'O' is the centre of the circle. OL and OM are perpendiculars from O to the chords AB and CD respectively. If OL=OM and AB=16cm, then find the length of CD.

View Solution
