$A (1, - 2) and B (2, 5)$ are two points. The lines $O A, O B$ are produced to $C and D$ respectively, such that $O C = 2 O A and O D = 2 O B$ . Find $C D$ .

Video Solution

Answer

Step by step video & image solution for A(1, -2) and B(2, 5) are two points. The lines OA, OB are produced to C and D respectively, such that OC=2OA and OD=2OB. Find CD. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Similar Questions

On the xy plane where O is the origin, given points, $A (1, 0), B (0, 1) and C (1, 1)$ . Let $P, Q, and R$ be moving points on the line $O A, O B, O C$ respectively such that $¯ ¯¯¯¯ ¯ O P = 45 t ¯ ¯¯¯¯¯¯¯ ¯ (O A), ¯ ¯¯¯¯ ¯ O Q = 60 t ¯ ¯¯¯¯¯¯¯ ¯ (O B), ¯ ¯¯¯¯ ¯ O R = (1 - t) ¯ ¯¯¯¯¯¯¯ ¯ (O C)$ with $t > 0 .$ If the three points $P, Q and R$ are collinear then the value of $t$ is equal to

A $\frac{1}{106}$
B $\frac{7}{187}$
C $\frac{1}{100}$
D none of these
View Solution
O is the origin and lines OA, OB and OC have direction cosines $l_{r}, m_{r} and n_{r} (r = 1, 2 and 3)$ . If lines OA', OB' and OC' bisect angles BOC, COA and AOB, respectively, prove that planes AOA', BOB' and COC' pass through the line $\frac{x}{l_{1} + l_{2} + l_{3}} = \frac{y}{m_{1} + m_{2} + m_{3}} = \frac{z}{n_{1} + n_{2} + n_{3}}$ .
View Solution
If $D$ , $E$ and $F$ are the mid-points of the sides $B C$ , $C A$ and $A B$ respectively of the $Δ A B C$ and $O$ be any point, then prove that $O A + O B + O C = O D + O E + O F$
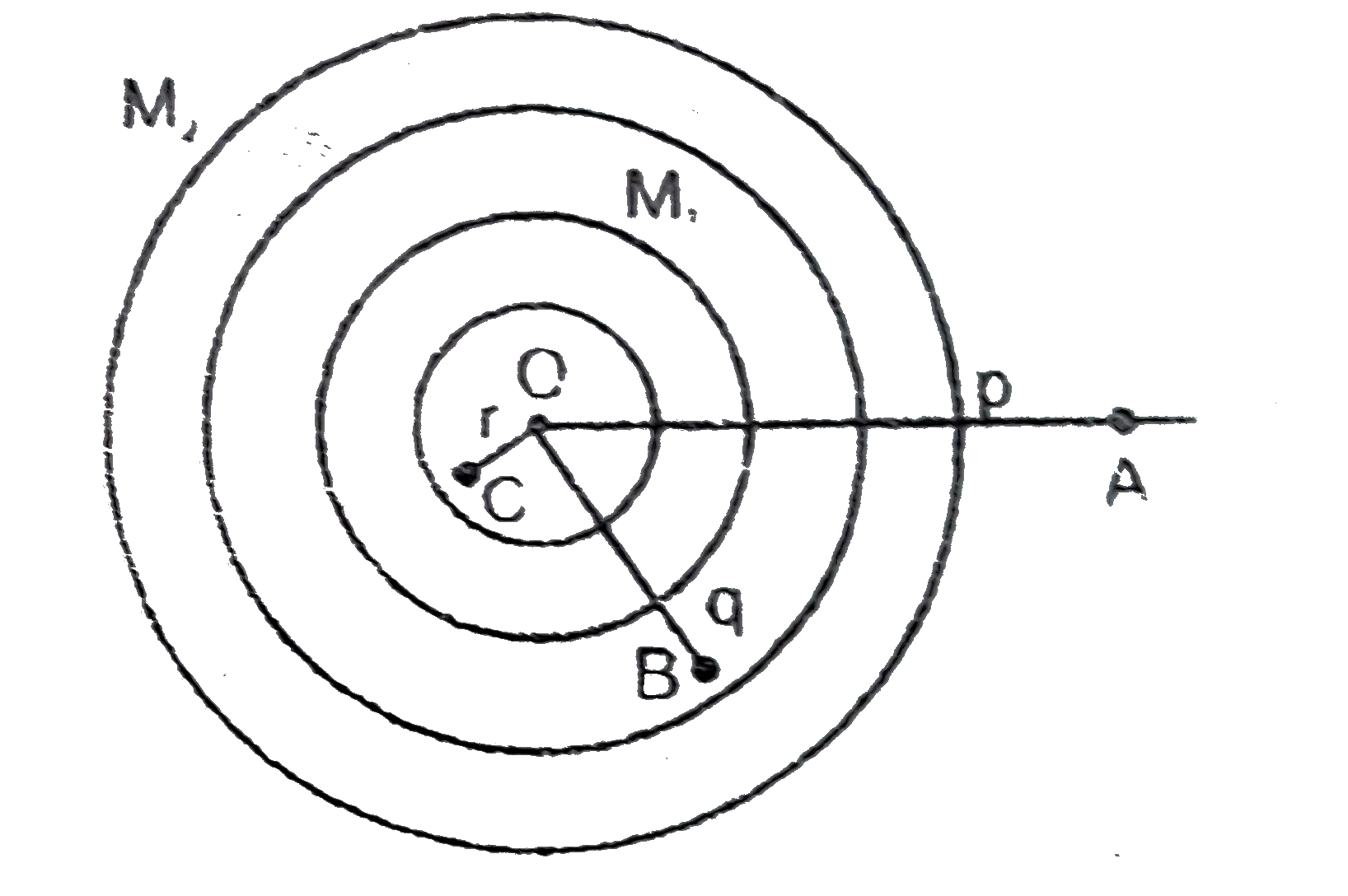
View Solution
Two concentric shells of uniform density of mass $M_{1}$ and $M_{2}$ are situated. The forces experienced by a particle of mass m when palced at positions $A, B$ and $C$ respectively are given OA =p,OB = q and OC =r .
.
View Solution
A line through the origin intersects $x = 1, y = 2 and x + y = 4$ , in $A, B and C$ respectively,such that $O A \cdot O B \cdot O C = 8 \sqrt{2}$ . Find the equation of the line.
View Solution
The following figure shows a trapezium ABCD in which AB is parallel to DC and AD= BC

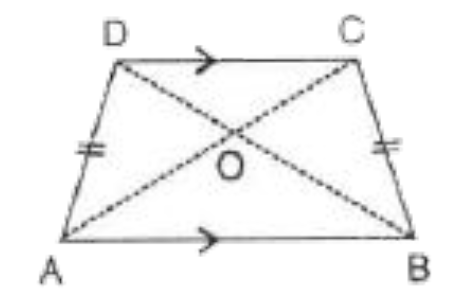
Prove that:
OA = OB and OC= OD
View Solution
Two particles $1$ and $2$ are allowed to descend on the two frictionless chord $O A$ and $O B$ of a vertical circle, at the same instant from point $O$ . The ratio of the velocities of the particles $1$ and $2$ respectively, when they reach on the circumference will be (OB is the diameter).
View Solution
In the figure, $O A$ and $O B$ are two uniformly charged wires, placed along $x$ and $y$ axis respectively. Find the unit vector in the direction of field at point $(0, 0, \sqrt{3 L})$ .

View Solution
Two fixed point $A and B$ are taken on the two axes such that $O A = a, O B = b$ , two variable points $C, D$ are taken on the same axes respectively, find the locus of the point of intersection of $A D and C B$ if : $\frac{1}{O} C - \frac{1}{O} D = \frac{1}{O} A - \frac{1}{O} B$
View Solution
A and B are two points on the parabola $y^{2} = 4 a x$ with vertex O. if OA is perpendicular to OB and they have lengths $r_{1}$ and $r_{2}$ respectively, then the valye of $\frac{r_{1}^{4 / 3} r_{2}^{4 / 3}}{r_{1}^{2 / 3} + r_{2}^{2 / 3}}$ is
View Solution

A ( 1 , - 2 ) and B ( 2 , 5 ) are two points. The lines O A , O B are produced to C and D respectively, such that O C = 2 O A and O D = 2 O B . Find C D .

Similar Questions

Recommended Questions

$A (1, - 2) and B (2, 5)$ are two points. The lines $O A, O B$ are produced to $C and D$ respectively, such that $O C = 2 O A and O D = 2 O B$ . Find $C D$ .