ABC is a cyclic equailateral triangle. If D be any point on the circular are BC on the oppsite side of the point A, then prove that DA=DB+DCSolution in Bengali
Let ABC be a cyclic equailateral angle inside the circle with centre at O,D is any point on the circular are BC on the opposite side of the point A.
We have to prove that DA=DB+DC

Construction Let us cut a part De from DA equal to DC. i.e, DC= DE and let us join C,E
In ΔCDE,DC=DE [ as per construction]
∴∠DCE=∠DEC.....(1)
∴ΔABC is an equilateral triangle,
∠BAC=∠ACB=∠CBA=60∘andABBC=CA......(2)
Now, two angles in circle produced by the are AC are ∠ADCand∠ABC
∴∠ADC=60∘[ by (2)]
∴∠CDE=60∘......(3)
∴inΔCDE,∠CDE+∠DCE=180∘+∠DEC=180∘
or, 60∘+∠DCE+∠DCE=180∘[ from (1) and (3)]
or, 2∠DCE=180∘−60∘or,∠DCE=120∘2=60∘
∴∠DEC=60∘ i.,e, each and very angle of ΔCDE is 60∘,ΔCDE is equilateral.
∴CD=DE=CE....(4)
Now, ∠ACE+∠BCE=∠ACB=60∘=∠DCE=∠BCD+∠BCE
∴∠ACE=∠BCD........(5)
Again in Δ's ACE and ΔBCD
∠CAE=∠CBD[∴ bothare angles in cricle produced by the same chord CD]
∴∠ACE=∠BCD [by (5)] and AC=BC [ ∴ΔABC is equilateral]
∴ΔACE≅BCD[∴ by the A-A-S condition of congruency]
∴AE=BD[∴ similar sides of congruent tirangles]........(6)
Therefore, DA=DE+AE=DC+BD[∴DE=DCandAE=BD]
Hence DA=DB+DC
Topper's Solved these Questions
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (True or False)4videos
THEOREMS RELATED TO ANGLES IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short-Answer Type Questions) MCQs5videos
THEOREMS RELATED TO ANGLES IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short Answer Type Questions)5videos
THEOREMS RELATED TO ANGLES IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Long -answer type questions (L.A.)12videos
THEOREMS RELATED TO CYCLIC QUADRILATERAL
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.223videos
THEOREMS RELATED TO TANGENT IN A CIRCLE
Similar Questions
In the adjoining figure AD and BE are perpendicular ot BC and AC respectively of the ΔABC. The four points A,B,D,E are concylic.
02:54View SolutionIn the adjoining figure, O is the centre of the circle AC is a diameter and chord DE is parallel to the diameter AC. If ∠CBD=60∘ , find the value of ∠CDE
08:04View SolutionIn the adjacent figure O is the centre of the circle. If ∠OAB=30∘,∠ABC=120∘,∠BCO=y∘and∠COA=x∘, then the find value sof x and y.
03:01View SolutionIn a cyclic quadrilateral, the ratio of three consecutive angle is 1 : 2 : 3 Find the value of first and third angles.
05:12View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
03:11View SolutionIn Fig. 4.132, if AD⊥BC and BDDA=DADC , prove that ABC is a right triangle. (FIGURE)
03:11View SolutionA point D is on the side BC of an equilateral triangle ABC such that DC=14 BC . Prove that AD2=13 CD2 .
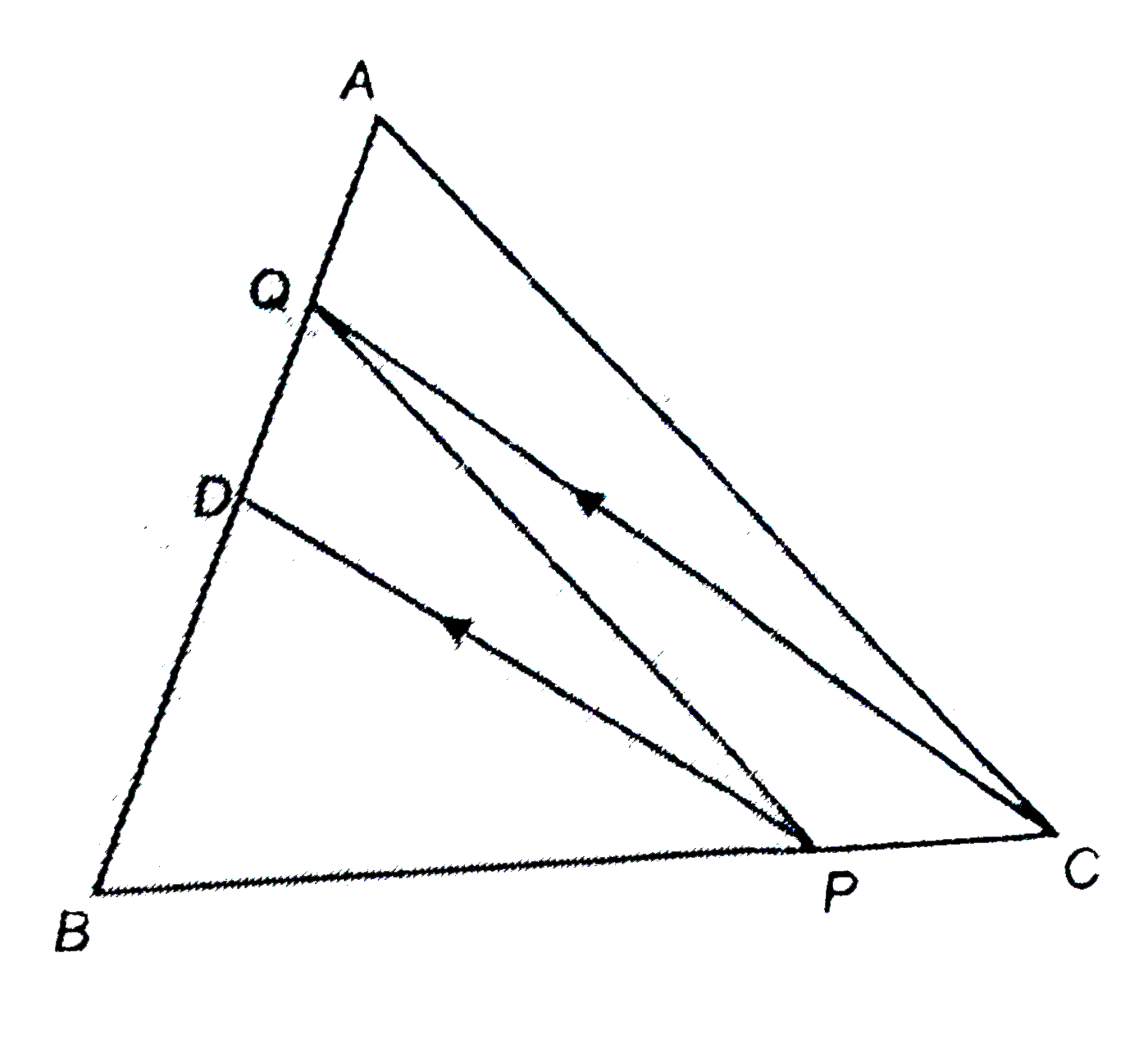
07:07View SolutionIn the adjoining figure, D is the mid-point of side AB of ΔABC and P be any point on side BC. If CQ∣∣PD, then prove that:
area of ΔBPQ=12× area of ΔABC
 05:04View Solution
05:04View Solutionकिसी △ABC में, D, भुजा BC का मध्य बिंदु इस प्रकार है कि BDDC=ABAC सिद्ध कीजिए कि AD, ∠A का अर्द्धक है |
08:49View Solutionचित्र में यदि AD⊥BC और BDDA=DADC हो, तो सिद्ध करो की ΔABC एक समकोण त्रिभुज है|
03:42View Solutionचित्र में यदि AD⊥BC और BDDA=DADC हो, तो सिद्ध करो की ΔABC एक समकोण त्रिभुज है|
06:16View SolutionD त्रिभुज ABC की भुजा AB का मध्यबिंदु है। Pभुजा BC पर कोई बिंदु है। CQ को PD के समांतर खीची गाया है। सिध्द कीजिए। कि PQ त्रिभुज ABC को समध्दिभाजित करती है।
05:43View SolutionABC সমবাহু ত্রিভুজের AC বাহুর উপর D একটি বিন্দু এবং বর্ধিত BC বাহুর উপর অপর E একটি বিন্দু | প্রমাণ করো যে , BE>BD
05:33View Solutionत्रिभुज ABC में, भुजा BC पर बिन्दु D तथा E इस प्रकार है कि DB = DE = EC है। यदि ∠ADE=∠AED=θ हो, तो
04:57View SolutionΔABC में, भुजाओं AB तथा AC पर क्रमशः D तथा E बिंदु हैं। यदि AD×EC=AE×DB हो , तो सिद्ध कीजिए कि DE∣∣BC |
02:48View Solution

