Two identical rods each of mass m and length are connected as shown. Locate c.m.
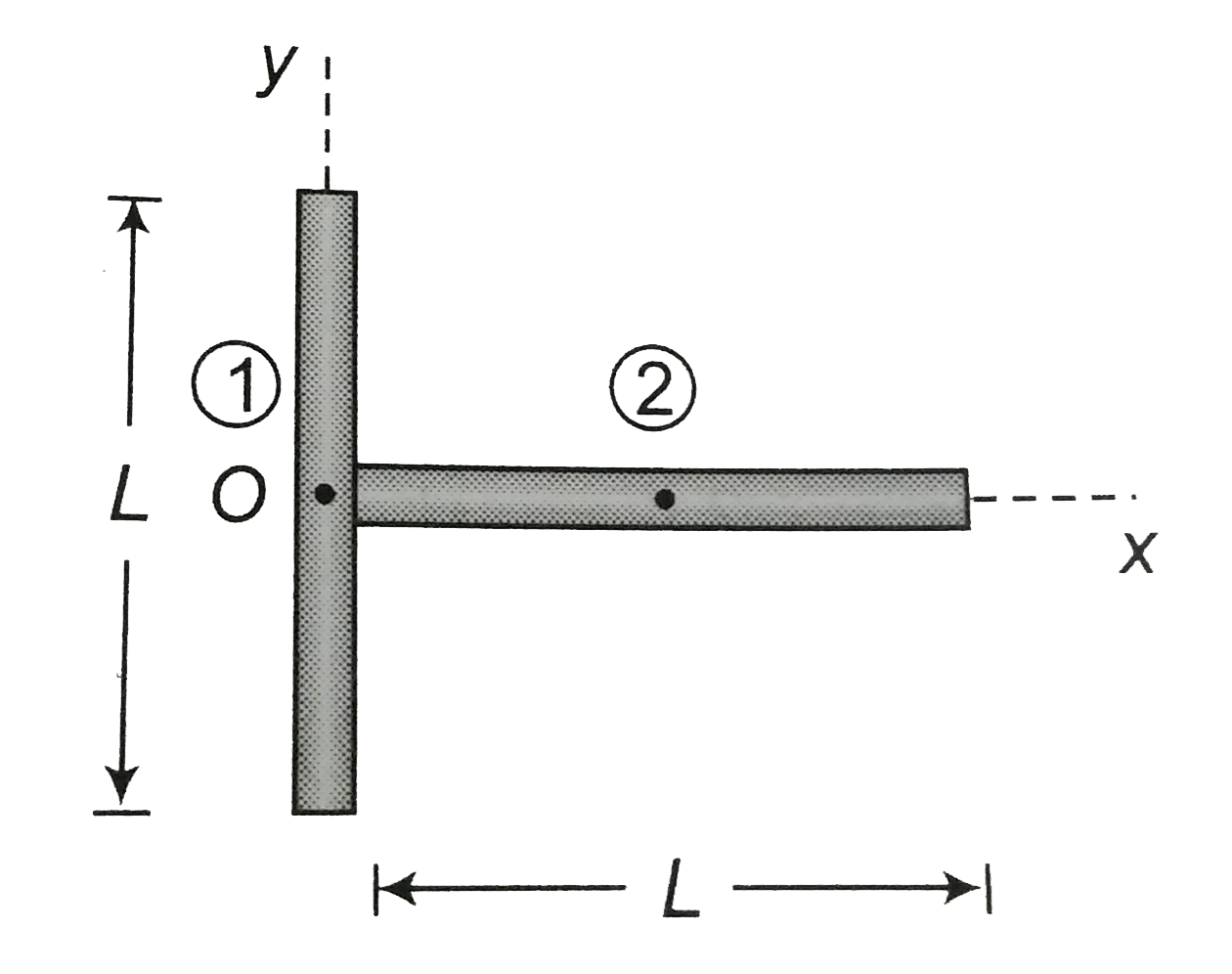
(a) This system is symmetrical about the x-axis . Hence we need to find xc.m.. Here we will take coordinates of c.m. of rods.
x−coordinateRod(1)m1=m0Rod(2)m2=mL2
xc.m.=m×0+m×L2m+m=mL22m=L4
yc.m.=0
c.m.≡(L4,0)
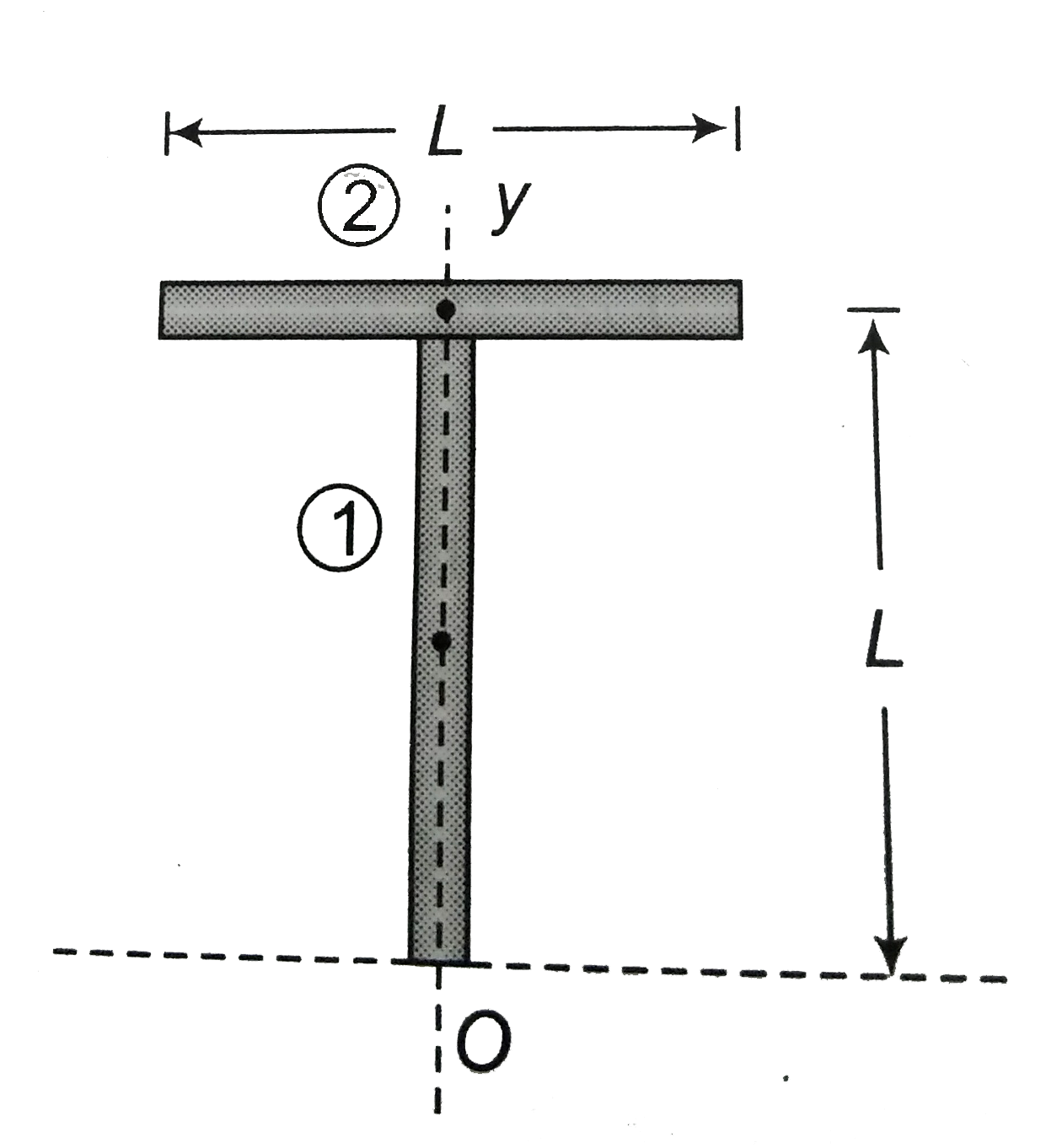
(b) Symmetry about the y-axis:
y−coordinateRod(1)m1=mL2Rod(2)m2=m(L)
yc.m.=m×L2+m×Lm+m=3L4
(c ) Symmetry about the y-axis:
y−coordinateRod(1)m1=mL2cos60∘=L4Rod(2)m2=mL2cos60∘=L4
yc.m.=m×L4+m×L4m+m=L4
(d) Not symmetrical about any axis
xyRod(1)m1=mL20Rod(2)m2=m0L2
xc.m.=m×L2+m×0m+m=L4
yc.m.=m×0+m×L2m+m=L4
coordinates of c.m.≡(L4,L4)


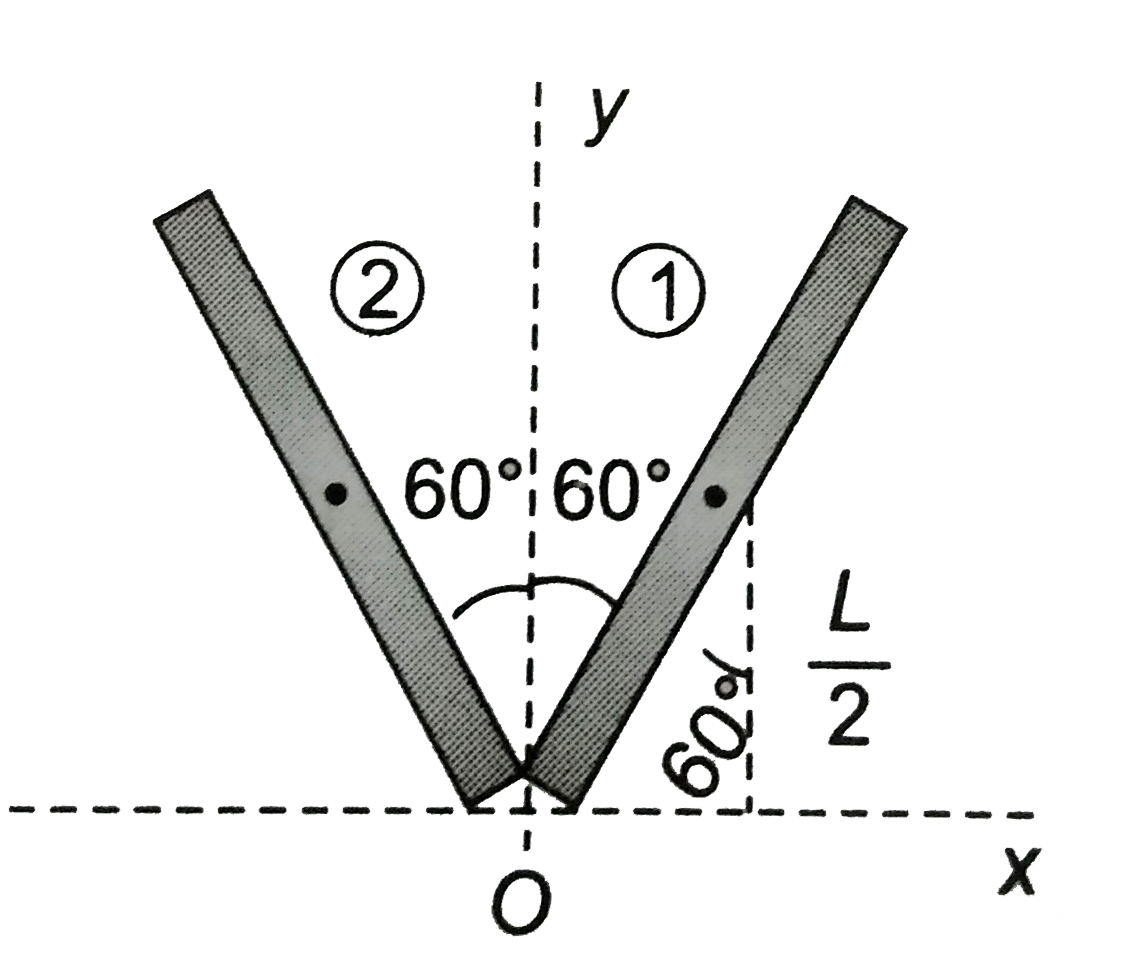


Topper's Solved these Questions
Similar Questions
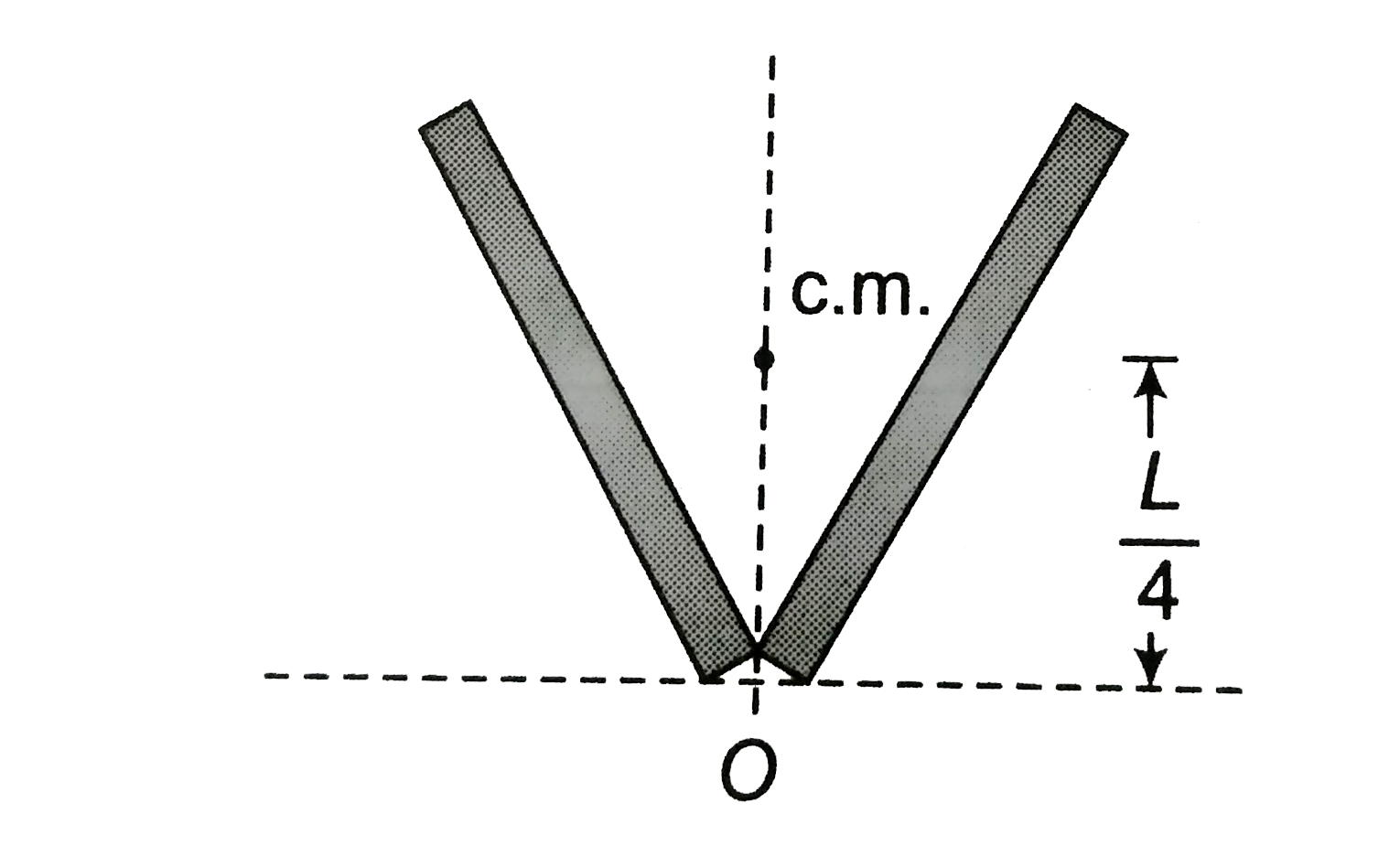
Two identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.
 View Solution
View SolutionTwo uniform identicla rods each of mass M and length l are joined to form a cross as shown in figure. Find the momet of inertia of the cross about a bisector as shown doted in the figure
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
For identical rods each of mass m and length l make a square frame in xy plane as shown. Calculate its momen of inertia about the x-axis.
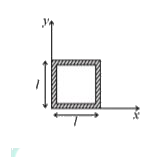 A53ml2B43ml2Cml2DNone of these
A53ml2B43ml2Cml2DNone of these - Question 2 - Select One
Two uniform thin identical rods AB and CD each of mass M and length L are joined so as to form as cross as shown. The monent of inertia of the cross about a bisector line EF is
 AML26BML24CML212DML23
AML26BML24CML212DML23 - Question 3 - Select One
Two uniform thin identical rods AB and CD each of mass M and length L are joined so as to form a cross as shown. The moment of inertia of the cross about a bisector line EF is :-
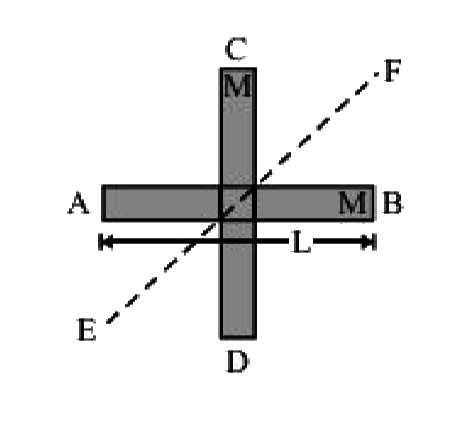 AML26BML24CML212DML23
AML26BML24CML212DML23
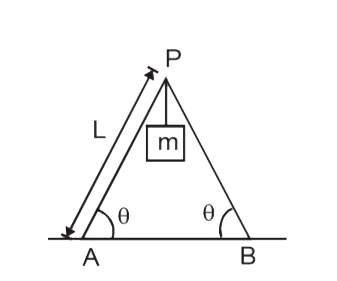
Two identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. If the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
 View Solution
View SolutionThree identical rods, each of mass m and length l are placed along x, y and z axis respectively. One end of each rod is at the origin. The moment of inertia of the rods x-axis will be
View SolutionFour identical rods of mass M and length L are placed on one another on the table so as to produce the maximum overhang as shown in figure. The maximum total overhang will be :
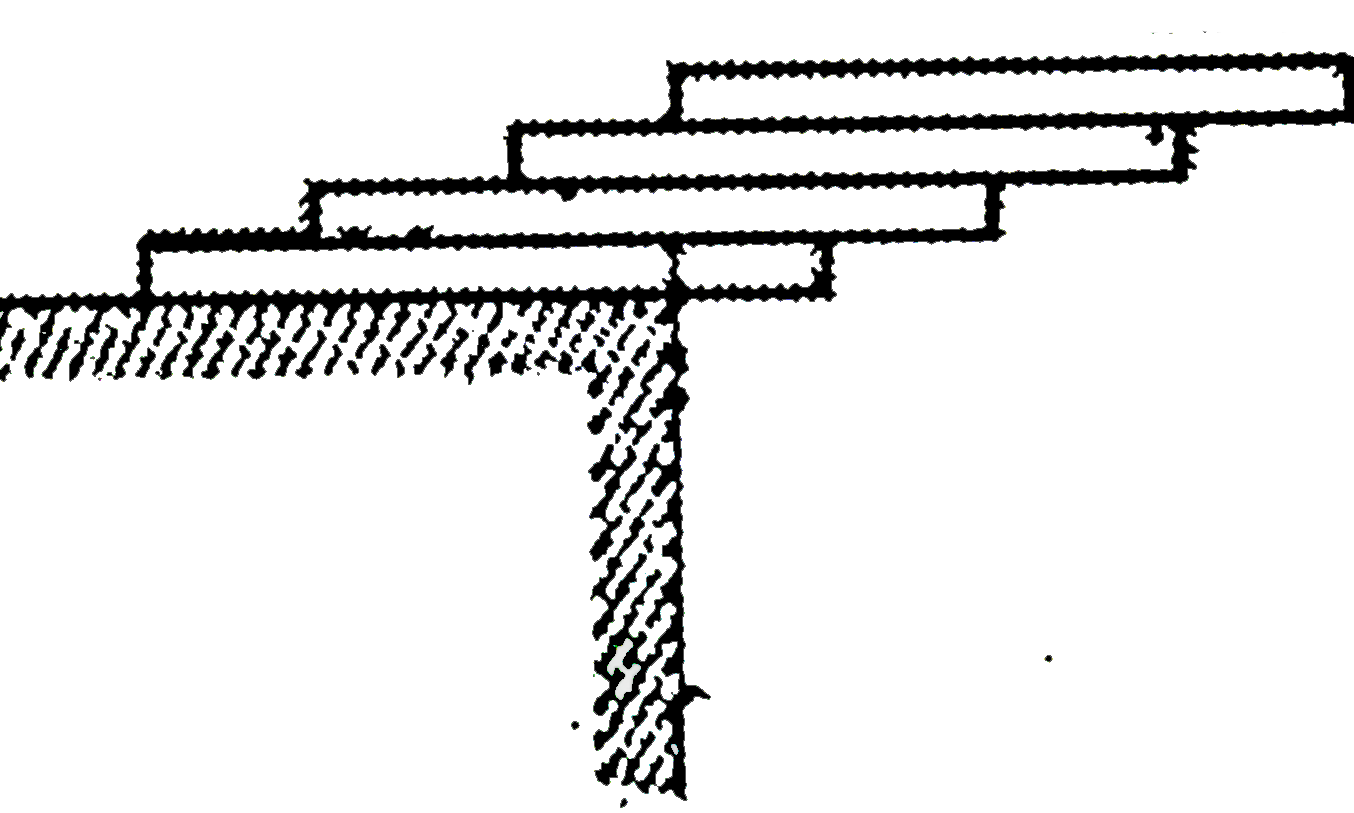 View Solution
View SolutionA system of two identical rods (L-shaped) of mass m and length l are resting on a peg P as shown in the figure. If the system is displaced in its plane by a small angle θ,find the period of oscillations:
 View Solution
View SolutionThree identical rods, each of mass m and length l, form an equaliteral triangle. Moment of inertia about one of the sides is
 View Solution
View Solution

