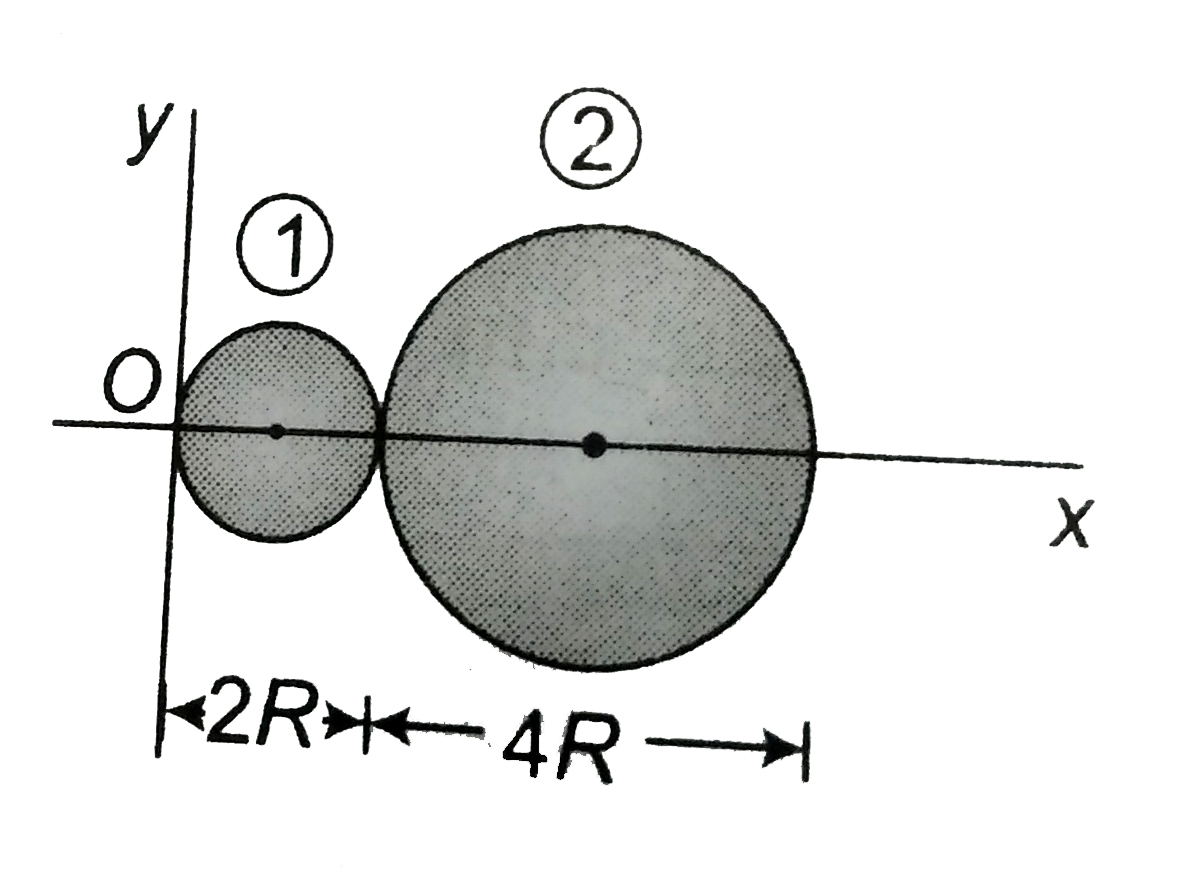
Two uniform discs made of same material and thickness of redii R and 2R are joined as shown. Locate c.m.

This diagram is symmetrical about the x-axis.
Mass=density×volume=density×area×thickness
Here , density and thickness is same , hence mass α area
Disc(1),m1∝πR2⇒m1=k×πR2
⇒m1=m,x1=R
Disc(2),m2∝π(2R)2⇒m2=k×4πR2
⇒m2=4m,x2=2R+2R=4R
xc.m.=m1x1+m2x2m1+m2=m×R+4m×4Rm+4m
=17R5=3.4R
Center of mass from the center of smaller disc, i.e. from O1 is
3.4R−R=2.4R
Center of mass from the contact point of disc , i.e. from O2 is
3.4R−2R=1.4R
Center of mass from the center of the larger disc , i.e. from O3 is
4R−3.4R=0.6R Note : In general , assume reference axes , as explained previously but in the question if the reference point is given , e.g. locate c.m. from center of smaller disc. You can assume center of smaller disc as origin.
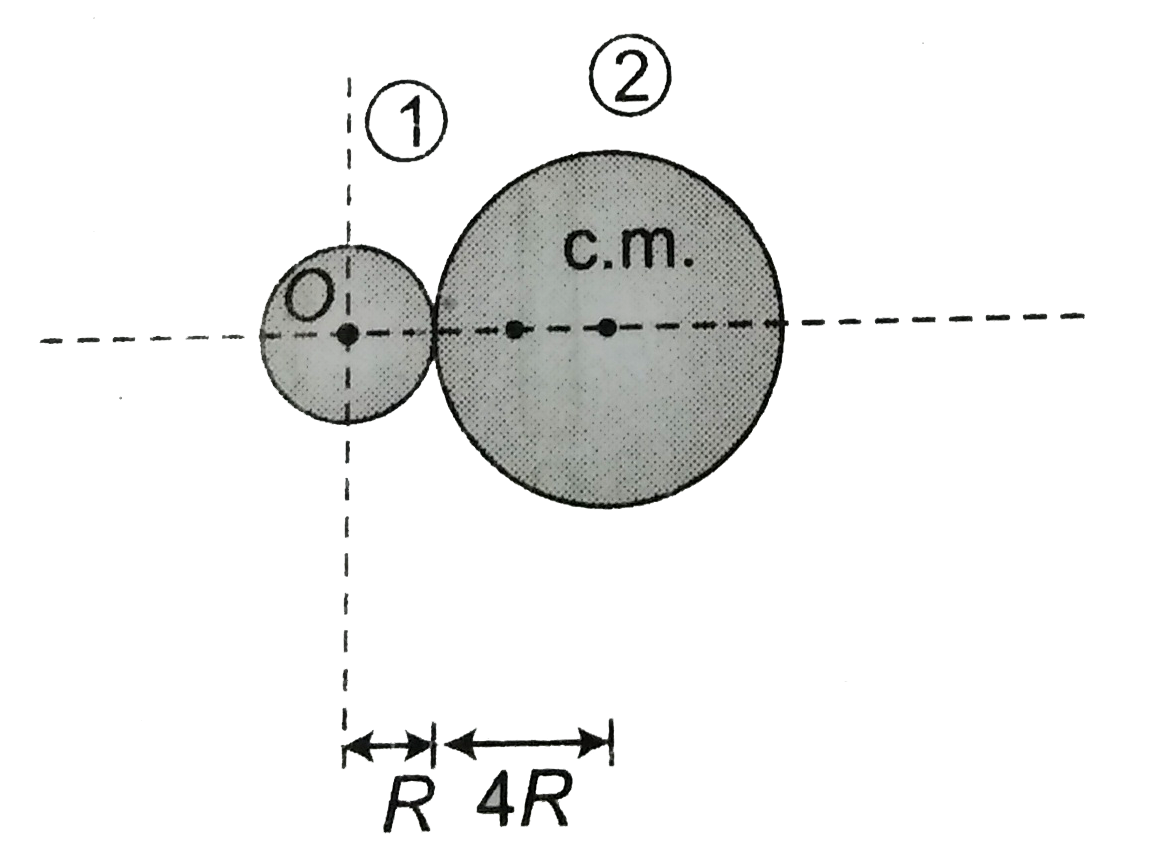
m1=mx−coordinate0m2=4mR+2R=3R
xc.m.=m×0+4m×3Rm+4m=12R=2.4R
c.m. from joining point of discs :
x−coordinatem1=m−Rm2=4m2R
xc.m.=m×(−R)+4m×2Rm+4m=7R5=1.4R
c.m. from center of large disc :
x−coordinatem1=m−(2R+R)=−3Rm2=4m0
xc.m.=m(−3R)+4m×0m+4m
=−3R5=−0.6R
The −ve sign indicates that c.m. will be on the left of O. Note that c.m. will be nearer to the c.m. of larger mass.
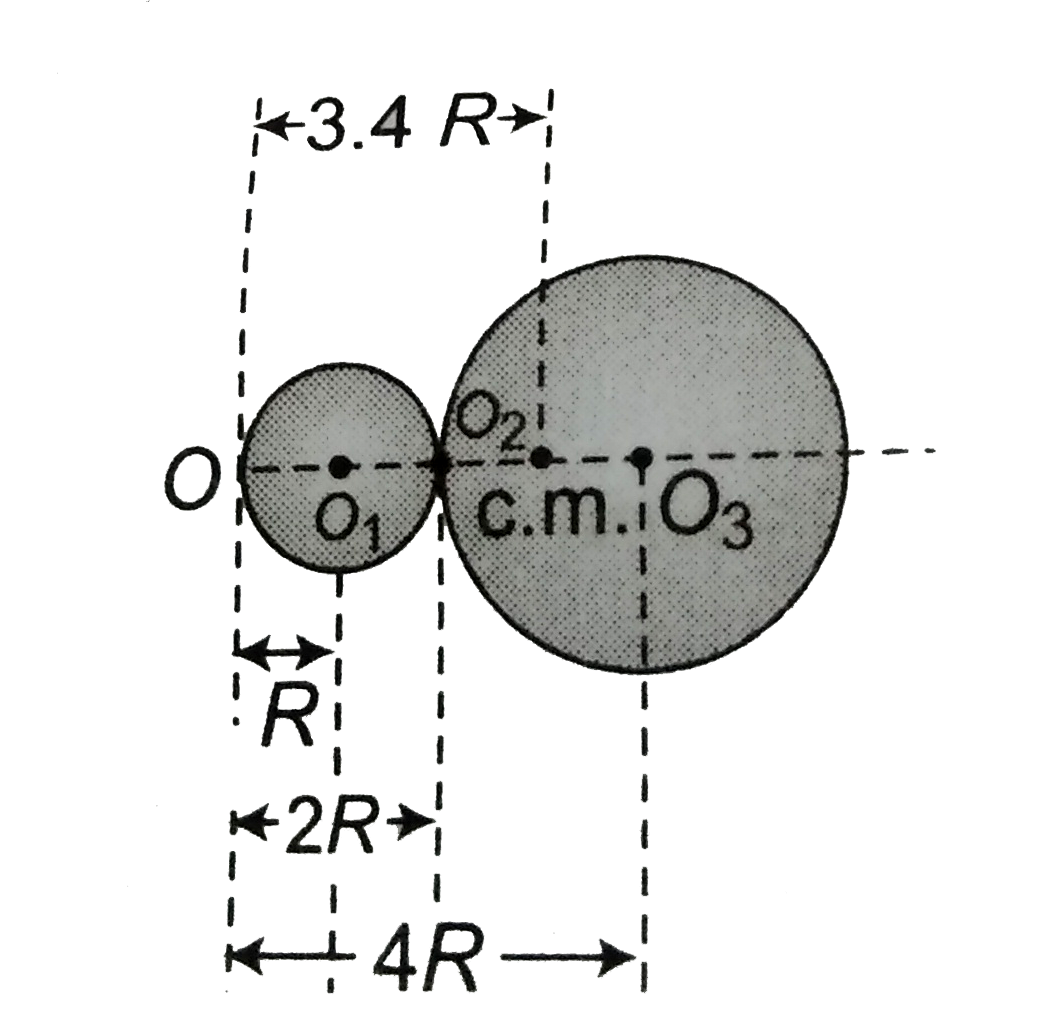

Topper's Solved these Questions
Similar Questions
Two thin uniform rings made of same material and of radii R and 4R are joined as shown. The mass of smaller ring is m. Find the M.I. about an axis passing through the center of mass of system of rings and perpendicular to the plane.
View SolutionTwo metallic cylinder made of same material and radii r and 2r are joined as shown in figure. If top end is ved and lower end of cylinder B is twisted by angle e, then angle of twist for cylinder A is (both cylinder have fixed and

View Solution
Knowledge Check
Two disc made of same material and same thickness having radius R and μR.Their moment of inertia about their own axis are in ratio 1:16. Calculate the value of α
A2B12C1D14Three thin uniform rods made of same material are joined as shown. Locate x coordinate of COM.
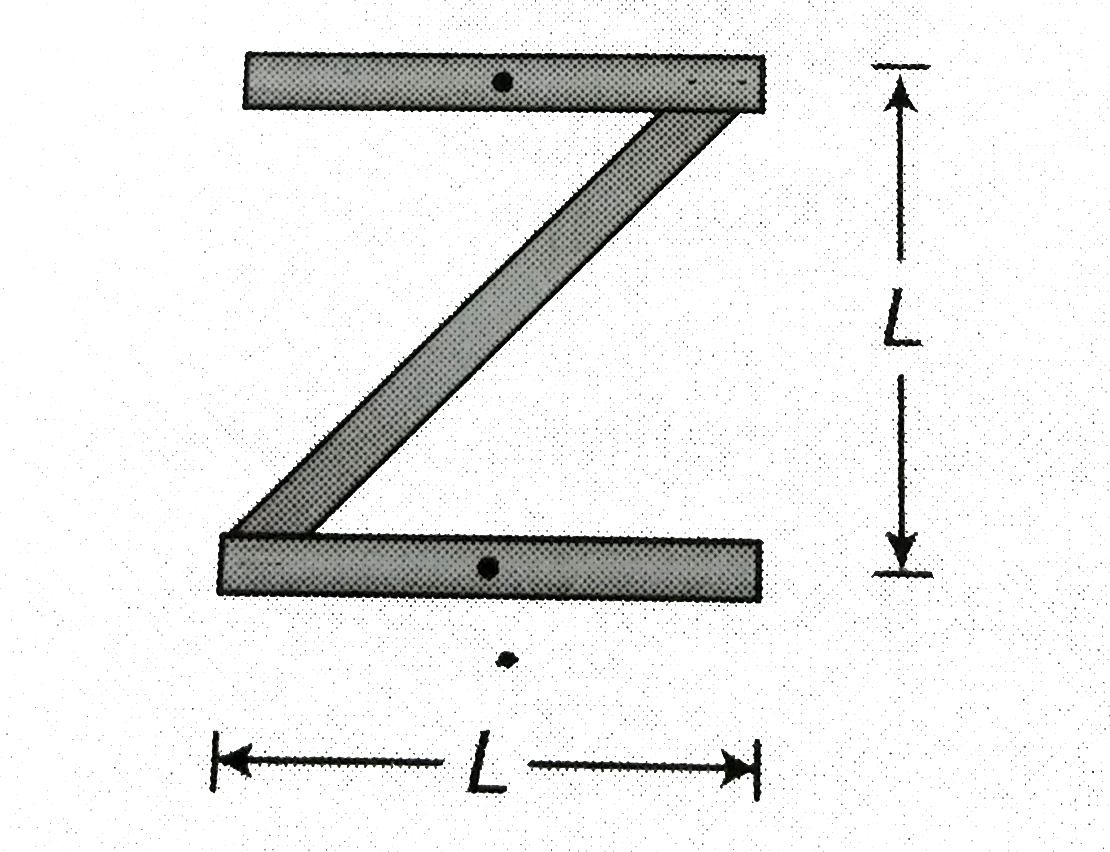 AL/2BL/3CL/4DL
AL/2BL/3CL/4DLTwo rods of same material and thickness are joined as shown below. The ends X and Y are maintained at X∘C and Y∘C respectively. The ratio of the heat flow in the two rods is –
 A0.36B0.64C10.36D1
A0.36B0.64C10.36D1
Two plates made of the same material and thickness are joined as shown. One plate is circular and another square in shape. The diameter of circular plate is equal to the side of the square plane. Locate c.m.

View SolutionTwo discs of the same material and thickness have radii 0.2 m and 0.6 m. Their moments of inertia about their axes will be in the ratio of
View SolutionConsider two uniform discs of the same thickness and different radii R1=R and R2=αR made of the same material. If the ratio of their moments of inertia I1andI2, respectively, about their axes is I1:I2=1:16 then the value of α is :
View SolutionTwo discs A and B have same mass and same thickness. If d1 and d2 are the densities of the materials of the discs A and B respectively, then the ratio of the moment of inertia of the discs A and B about their geometrical axis is
View SolutionTwo rods made of same material having same length and diameter are joined in series. The thermal power dissipated through then is 2W.If they are joined in parallel, the thermal power dissipated under the same conditions on the two ends of the rods, will be :
View Solution
