Two rods made of same material having same length and diameter are joined in series. The thermal power dissipated through then is 2W.If they are joined in parallel, the thermal power dissipated under the same conditions on the two ends of the rods, will be :
16 W
8 W
4 W
2 W
The correct Answer is:B
To solve the problem step by step, we will analyze the thermal power dissipation in both series and parallel configurations of the two rods.
Step 1: Understand the Series Configuration
When the two rods are connected in series, the total thermal resistance (R_total) is the sum of the individual resistances of the rods.
For each rod:
- Let R1=LkA (where L is the length, k is the thermal conductivity, and A is the cross-sectional area).
- Since both rods are identical, R2=R1.
Thus, the total resistance in series is:
Rtotal=R1+R2=R1+R1=2R1=2(LkA)
Step 2: Calculate Thermal Power in Series
The thermal power (P) dissipated through the rods in series can be expressed as:
P=ΔTRtotal
Given that the power is 2 W:
2=ΔT2(LkA)
From this equation, we can express ΔT:
ΔT=2⋅2(LkA)=4LkA
Step 3: Understand the Parallel Configuration
When the two rods are connected in parallel, the total resistance (R_parallel) can be calculated using the formula for resistors in parallel:
1Rparallel=1R1+1R2
Since R1=R2:
1Rparallel=1R1+1R1=2R1
Thus,
Rparallel=R12=L2kA
Step 4: Calculate Thermal Power in Parallel
The thermal power in the parallel configuration can be expressed as:
Pparallel=ΔTRparallel
Substituting Rparallel:
Pparallel=ΔTL2kA=ΔT⋅2kAL
Step 5: Relate Thermal Power in Parallel to Series
Now we can substitute ΔT from the series configuration into the equation for parallel:
Pparallel=(4LkA)⋅2kAL
This simplifies to:
Pparallel=4⋅2=8W
Final Answer
Thus, the thermal power dissipated when the rods are joined in parallel is:
8W
When the two rods are connected in series, the total thermal resistance (R_total) is the sum of the individual resistances of the rods.
- Let R1=LkA (where L is the length, k is the thermal conductivity, and A is the cross-sectional area).
- Since both rods are identical, R2=R1.
Rtotal=R1+R2=R1+R1=2R1=2(LkA)
The thermal power (P) dissipated through the rods in series can be expressed as:
P=ΔTRtotal
Given that the power is 2 W:
2=ΔT2(LkA)
From this equation, we can express ΔT:
ΔT=2⋅2(LkA)=4LkA
When the two rods are connected in parallel, the total resistance (R_parallel) can be calculated using the formula for resistors in parallel:
1Rparallel=1R1+1R2
Since R1=R2:
1Rparallel=1R1+1R1=2R1
Thus,
Rparallel=R12=L2kA
The thermal power in the parallel configuration can be expressed as:
Pparallel=ΔTRparallel
Substituting Rparallel:
Pparallel=ΔTL2kA=ΔT⋅2kAL
Now we can substitute ΔT from the series configuration into the equation for parallel:
Pparallel=(4LkA)⋅2kAL
This simplifies to:
Pparallel=4⋅2=8W
Thus, the thermal power dissipated when the rods are joined in parallel is:
8W
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Advance MCQs with One or More Option Correct20videos
HEAT TRANSFER
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO66videos
HEAT TRANSFER
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Conceptual MCQs Single Option Correct24videos
HEAT TRANSFER
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO82videos
HEAT AND THERMAL EXPANSION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO64videos
Kinetic Theory of Gases and Gas Laws
Similar Questions
Two rods of the same length and material transfer a given amount of heat in 12 seconds when they are joined end to end. But when they are joined lengthwise, they will transfer the same amount of heat, in the same conduction, in :
View SolutionThree rods A,B and C of the same length and cross- sectional area are joined in series as shown. The temperature at the junction of A and B, in equilibriu, is
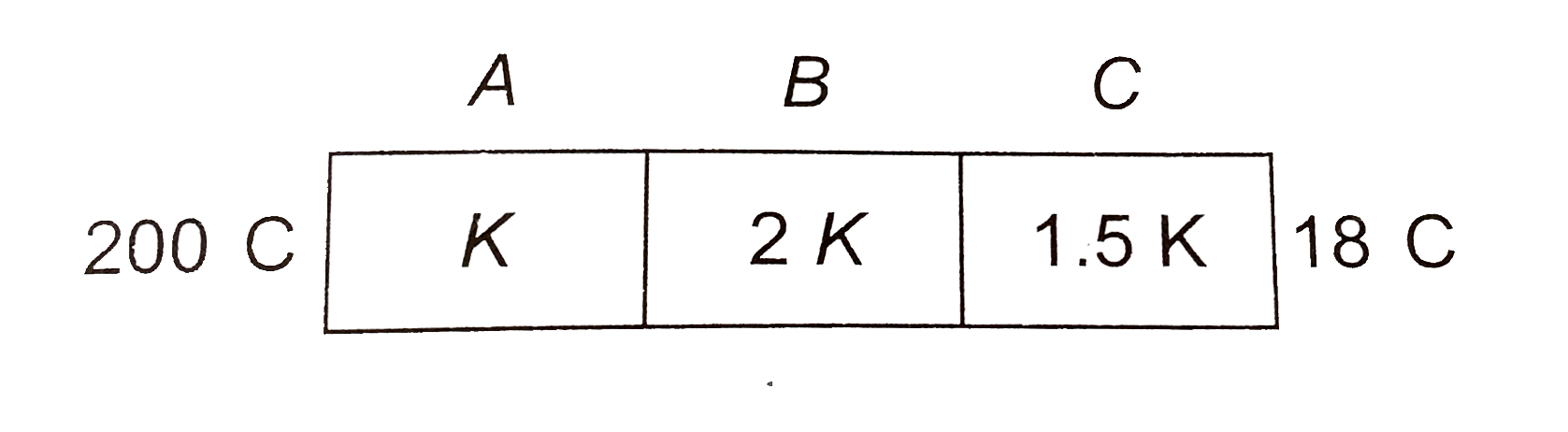 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two rods are of same material and having same length and area. If heat ΔQ flows through them for 12 min when they are joined side by side. If now both the rods are joined in parallel, then the same amount of heat ΔQ will flow in
A24 minB3 minC12 minD6 min - Question 2 - Select One
Two rods of same length and material transfer given amount of heat in 12 s, when they are joined end to end. When they are joined parallelly then they will transfer same amount of heat in same conditions in
A1.5sB3sC24sD48s - Question 3 - Select One
Two rods of equal length and diameter have thermal conductivity 3 and 4 units respectively. If they are joined in series, the thermal conductivity of the combination in the given units would be
A3.43 unitsB4.43 unitsC5.43 unitsD2.43 units
Two rods of same material and length have their electric resistance in ratio 1:2. When both rods are dipped in water, the correct statement will be
View SolutionTwo rods of the same length and diameter having thermal conductivities K1 and K2 are joined in parallel. The equivalent thermal conductivity of combination is
View SolutionTwo rods of the same length and diameter having thermal conductivities K1 and K2 are joined in parallel. The equivalent thermal conductivity of combination is
View SolutionTwo rods of the same length and diameter, having thermal conductivities K1 and K2, are joined in parallel. The equivalent thermal conductivity to the combinationk is
View SolutionTwo rods of equal length and diameter but of thermal conductivities 2 and 3 unites respectively are joined in parallel. The thermal conductivity of the combination is:
View Solution

