A uniform chain of mass M and length L is held vertically in such a way that its lower end just touches the horizontal floor. The chain is released from rest in this position. Any portion that strikes the floor comes to rest. Assuming that the chain does not form a heap on the floor, calculate the force exerted by it on the floor when a length x has reached the floor.
Mass per unit length of chain =mL
Consider the small portion of length dx
dm=mLdx
Chain in the momentum of small portion in time dt
F=dpdt=dmvdt=mLdxdtv=mLv×v=mLv2
v=√2gL
Force exerted due to the change in momentum is
mL2gL=2mg
Weight of chain =mg
Total force =mg+2mg=3mg

Topper's Solved these Questions
Similar Questions
A very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
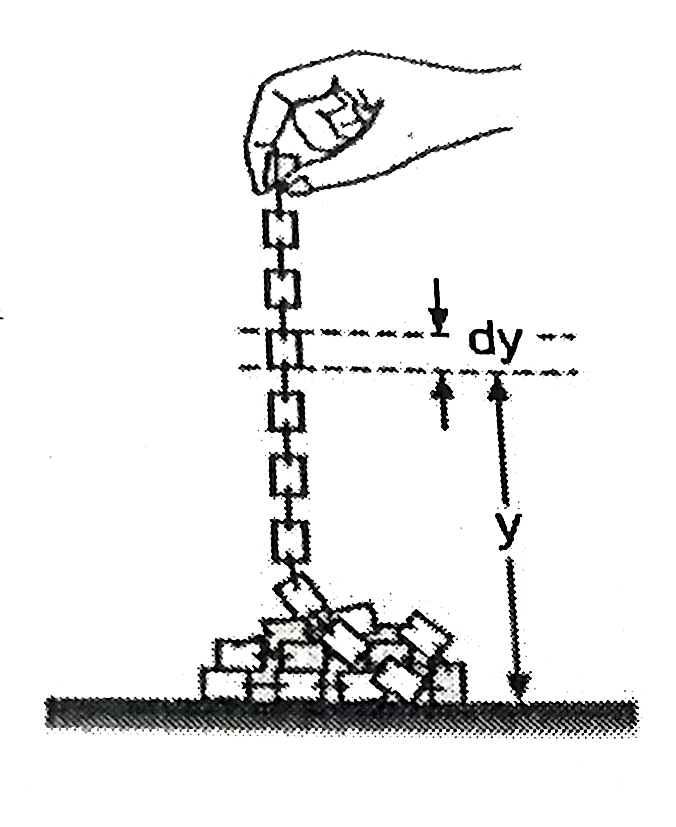 View Solution
View SolutionA very flexible uniform chain of mass M and length l is suspended vertically in a lift so that its lower end is just touching the surface of the floor. When the upper end of the chain is released, it falls with each link coming to rest the instant it strikes the floor of the lift.Find the force exerted by the floor of the lift on the chain at the moment, when one fourth of the chain has already rested on the floor. Assume that lift is moving up with an acceleration g/2.
View Solution
Knowledge Check
- Question 1 - Select One
A uniform chain of mass M and length L is held vertically in such a way that its lower end just touches the horizontal floor. The chain is released from rest in this position. Any portion that strikes the floor comes to rest. Assuming that the chain does not form a heap on the floor, calculate the force exerted by it on the floor when a length x has reached the floor.
A5 NB10 NC15 ND20 N - Question 2 - Select One
A chain of mass M and length l is held vertically such that its bottom end just touches the surface of a horizontal table. The chain is released from rest. Assume that the portion of chain on the table does not form a heap. The momentum of the portion of the chain above the table after the top end of the chain falls down by a distance l8.
A314M√glB316M√glC716M√glD914M√gl - Question 3 - Select One
A chain of mass M and length L is held vertical by fixing its upper end to a rigid support. The tension in the chain at a distance y from the rigid support is:
AMgBMg(L−y)/LCMgL/(L−y)DMgy/L
A very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
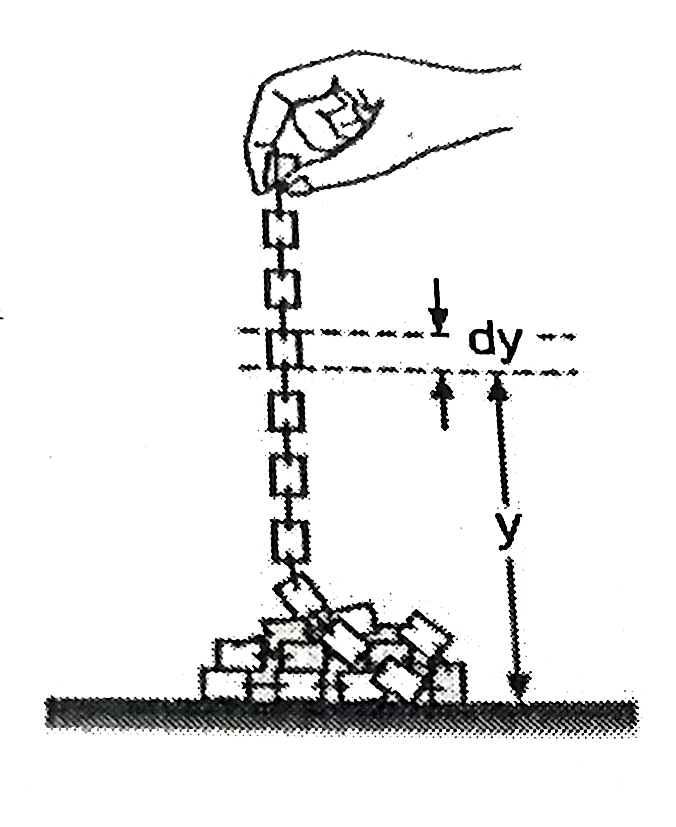 View Solution
View SolutionA uniform stick of mass M and length L is kept vertical on a frictionless horizontal floor. If the stick is allowed to fall, then mark the correct alternatives
View SolutionA very flexible chain of mass M and length l is suspended vertically in a lift so that its lower end is just touching the surface of the floor. When the upper end of the chain is released, it falls with each link coming to rest intantaneously find the force exerted by the floor of the lift on the chain at the moment when one fourth of the chain has already landed on the floor Assume the lift is moving with acceleration g/2
View SolutionA very flexible unifrom chain of mass M and length L is suspended vertically so that its lower end just touches the surface of a table When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table Find the force exerted by the chain on the table at the moment when x part of chain has already rested on the table .
View SolutionA rod of mass m and length l is held vertically on a smooth horizontal floor. Now it is released from this position, find the speed of its centre of mass when it makes an angle θ with the vertical.
View Solution

