A very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
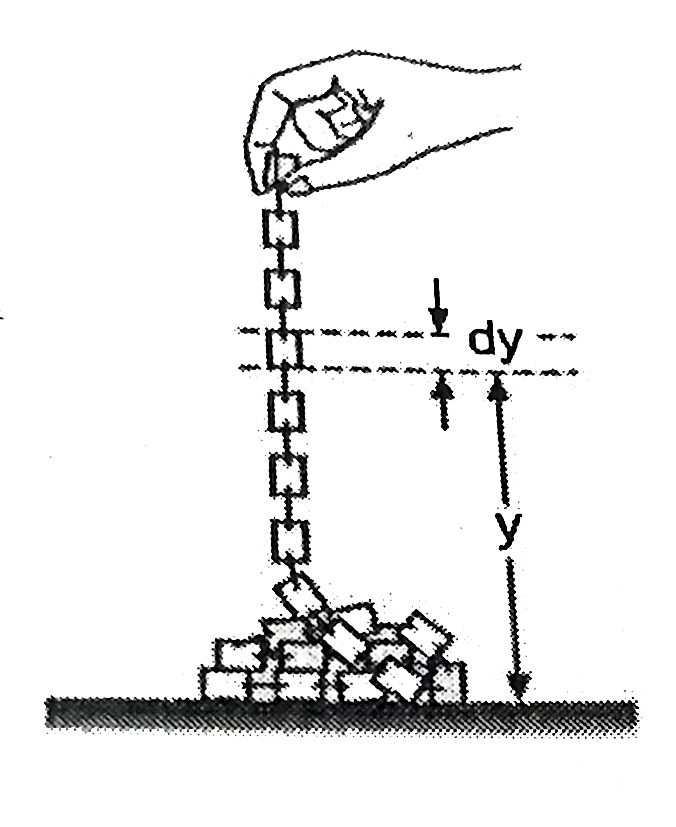
In this problem force on the table will be due to the weight of the chain on the table (sayF1) and also due to the momentum of chain being transmitted at each instant when the chain strikes it (sayF2) so that
F=F1+F2 ….(i)
Now as mass per unit length of the chain is (M/L) so when y length of the chain is on the table,
F1=(ML×y)g ....(ii)
Now to calculate F2 consider element dy at a height y above the table so that its mass will be (M/L) dy and it will hit the table, with a velocity v=√2gy so the momentum transmitted by it to the table,
dp=(dm)v=(M/L)dy√2gy
So that, F2=dpdt=MLdydt√2gy
or F2=ML2gy[asdydt=v=√2gy] ....(iii)
Substituting F1 and F2 from eqns (ii) and (iii) in (i) we get
F=3{MLyg}=3 [weight of chain on the table]
Note: Here as y=12gt2,F=3(Mg2t2/2L), i.e., force is time dependent and increases non linearly with time.
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Problem for practice
30 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Objective Questions
134 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- BASIC MATHEMATICSBOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice
35 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
Similar Questions
A very flexible unifrom chain of mass M and length L is suspended vertically so that its lower end just touches the surface of a table When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table Find the force exerted by the chain on the table at the moment when x part of chain has already rested on the table .
View SolutionA very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
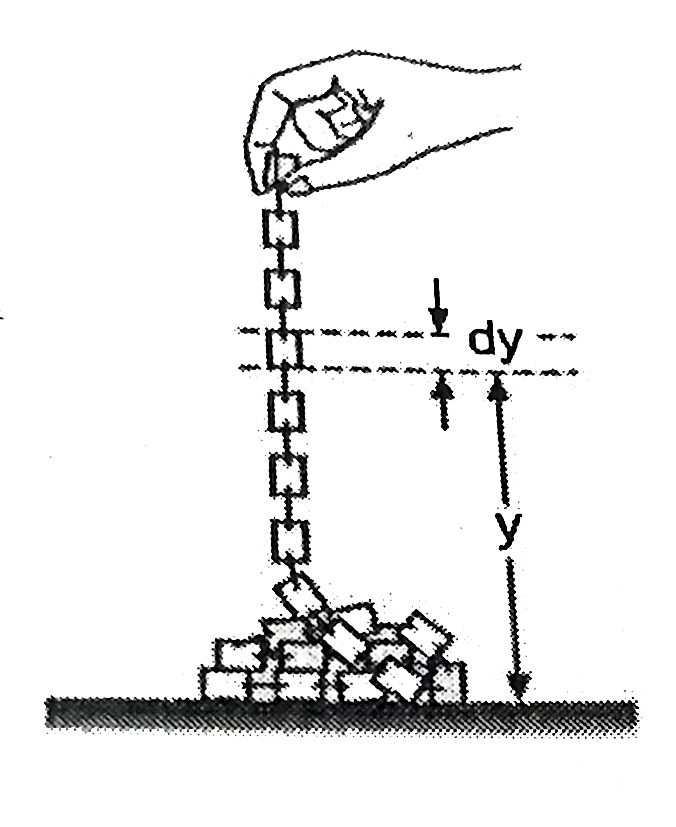
View Solution
Knowledge Check
A chain of mass M and length l is held vertically such that its bottom end just touches the surface of a horizontal table. The chain is released from rest. Assume that the portion of chain on the table does not form a heap. The momentum of the portion of the chain above the table after the top end of the chain falls down by a distance l8.
A314M√glB316M√glC716M√glD914M√gl
A very flexible chain of mass M and length l is suspended vertically in a lift so that its lower end is just touching the surface of the floor. When the upper end of the chain is released, it falls with each link coming to rest intantaneously find the force exerted by the floor of the lift on the chain at the moment when one fourth of the chain has already landed on the floor Assume the lift is moving with acceleration g/2
View SolutionA very flexible uniform chain of mass M and length l is suspended vertically in a lift so that its lower end is just touching the surface of the floor. When the upper end of the chain is released, it falls with each link coming to rest the instant it strikes the floor of the lift.Find the force exerted by the floor of the lift on the chain at the moment, when one fourth of the chain has already rested on the floor. Assume that lift is moving up with an acceleration g/2.
View SolutionA uniform chain of length l begins to fall with a velocity v on the table. Find the thrust force exerted by the chain on the table.
View SolutionA uniform chain of mass m and length l is placed on a smooth table so that one−third length hanges freely as shown in the figure. Now the chain is released, with what velocity chain slips off the table?

View SolutionA uniform chain of mass M and length L is held verticallyi in such a way that its lower end just touches the horizontal floor. The chain is released from rest in this position. Any portion that strikes the floor comes to rest. Assuming that the chain does not form a heap on the floor, calculate the force exerted by it on the floor when a length x has reached the floor.
View SolutionA uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

What is the speed of the chain, when it just loses contact with the table?
View SolutionA very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
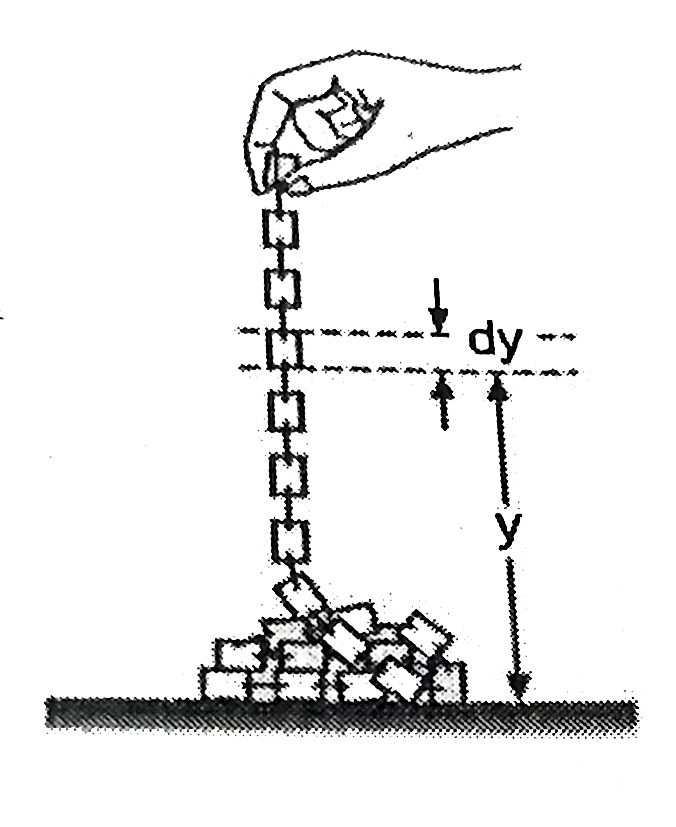
View Solution
