Find charge and potential on each capacitor. All capactances are in μF.
Video Solution
Text Solution
(a) 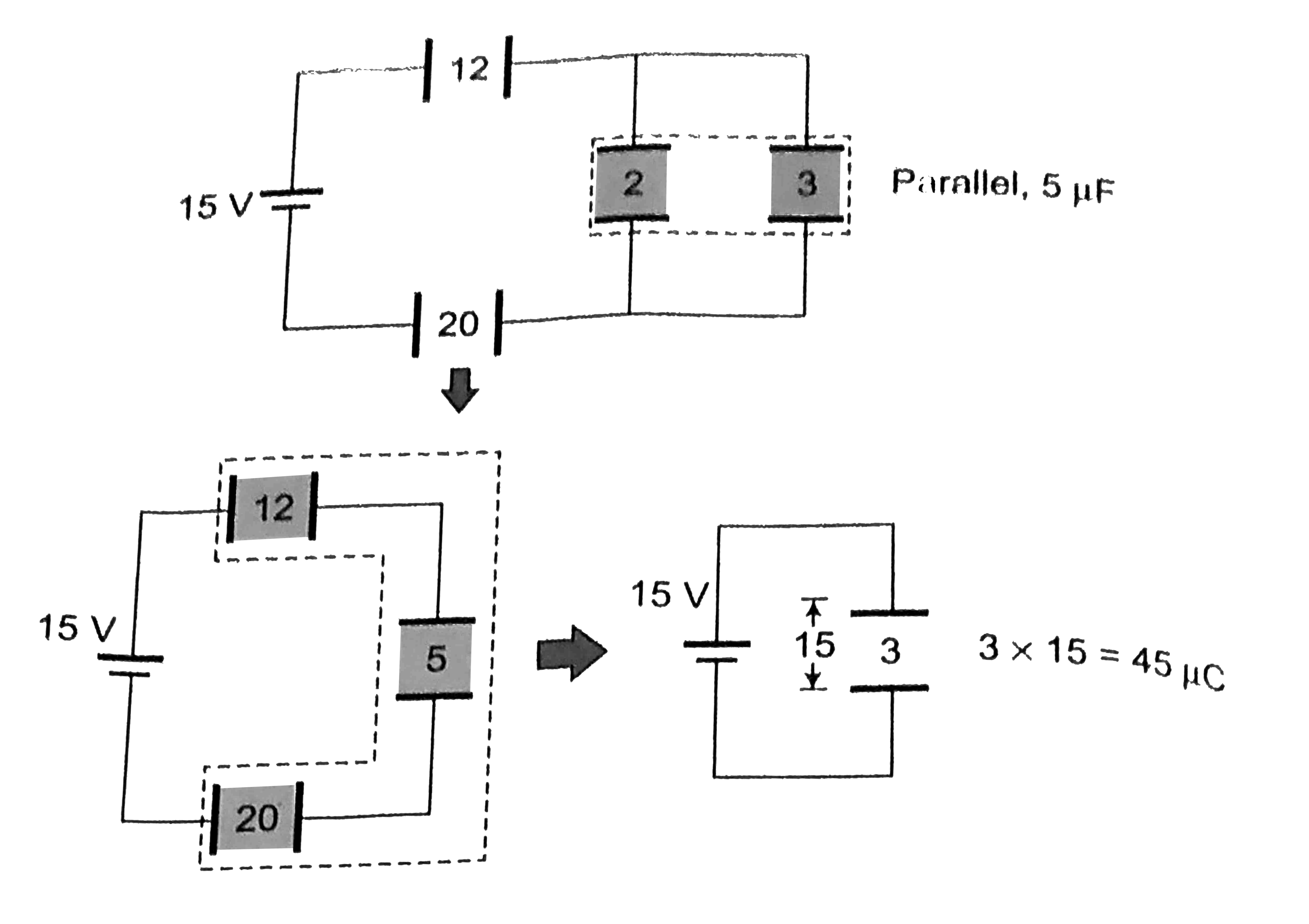
Series, 1Ceq=112+120+15
Ceq=3μF
Now return to previous diagrams.
Now return to previous diagram.
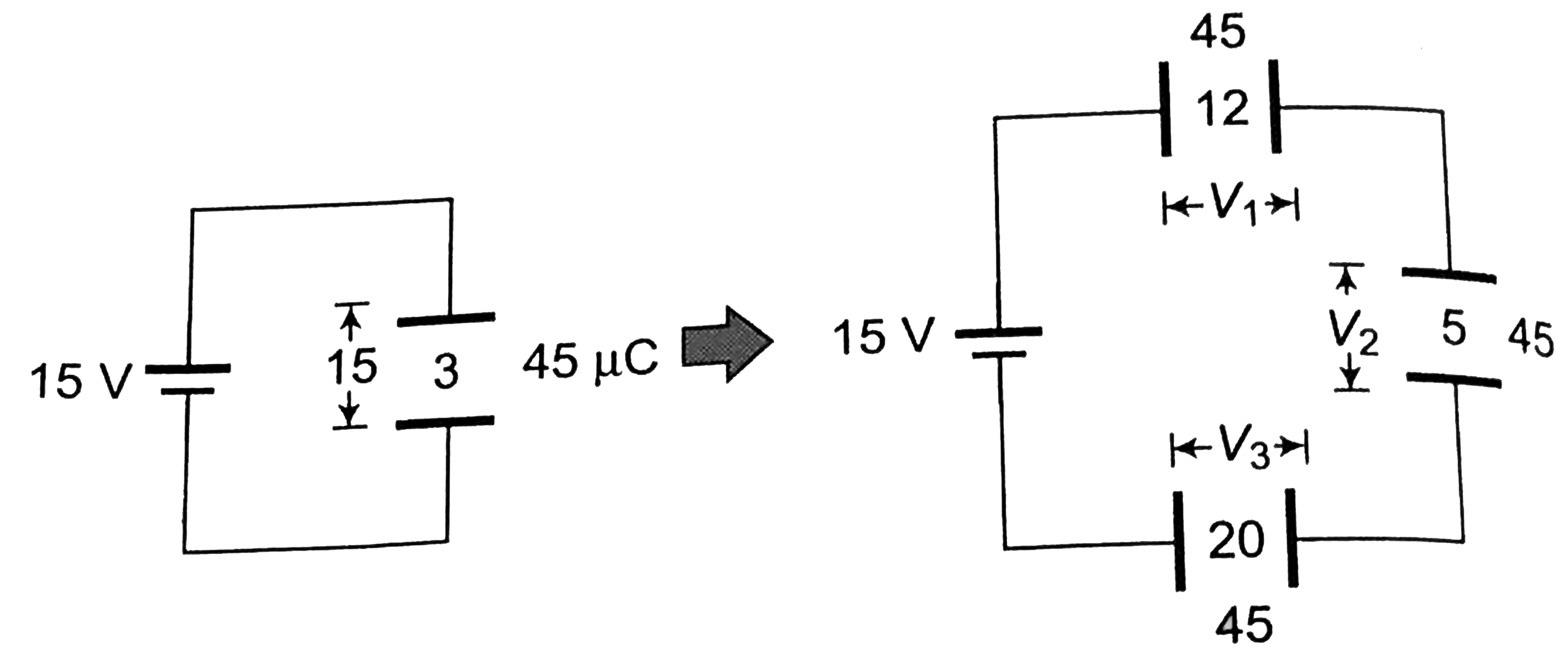
In series, charge on each capacitor is same and equal to charge on equivalent capacitance.
V1=4512=3.75V,V2=455=9V,V3=4520=2.25V

5μF is resultant of 2 and 3μF in parallel. In parallel potential on individual capacitors and equivalent capacitor is same. here potential on 5μF,2μF and 3μF will be same and equal to 9V.
(b) 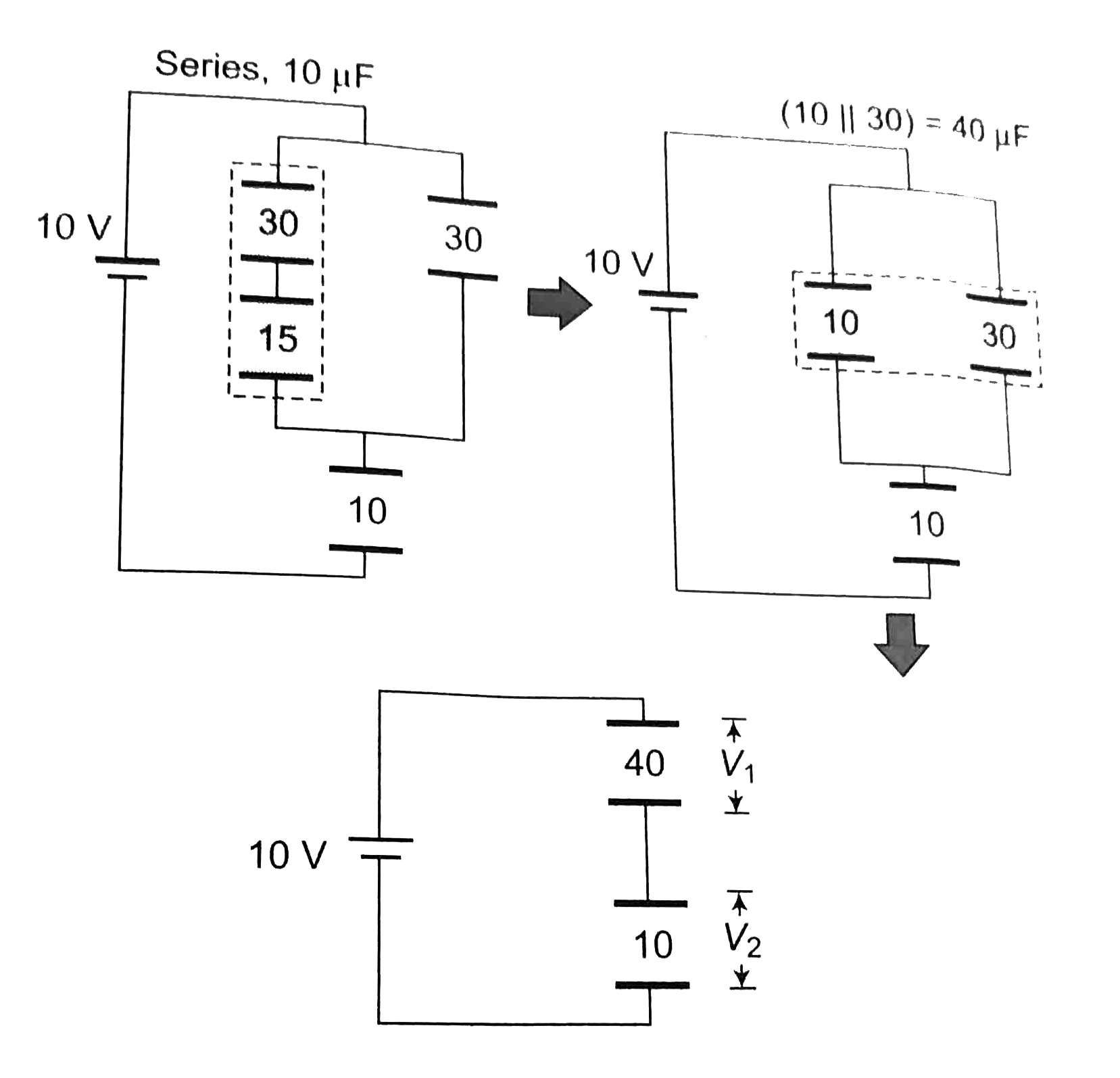
V1=(1010+40)×10=2V,V2=10−V1=8V
Now, return to previous diagram keeping in mind that in parallel, potential is same and in series charge is same.
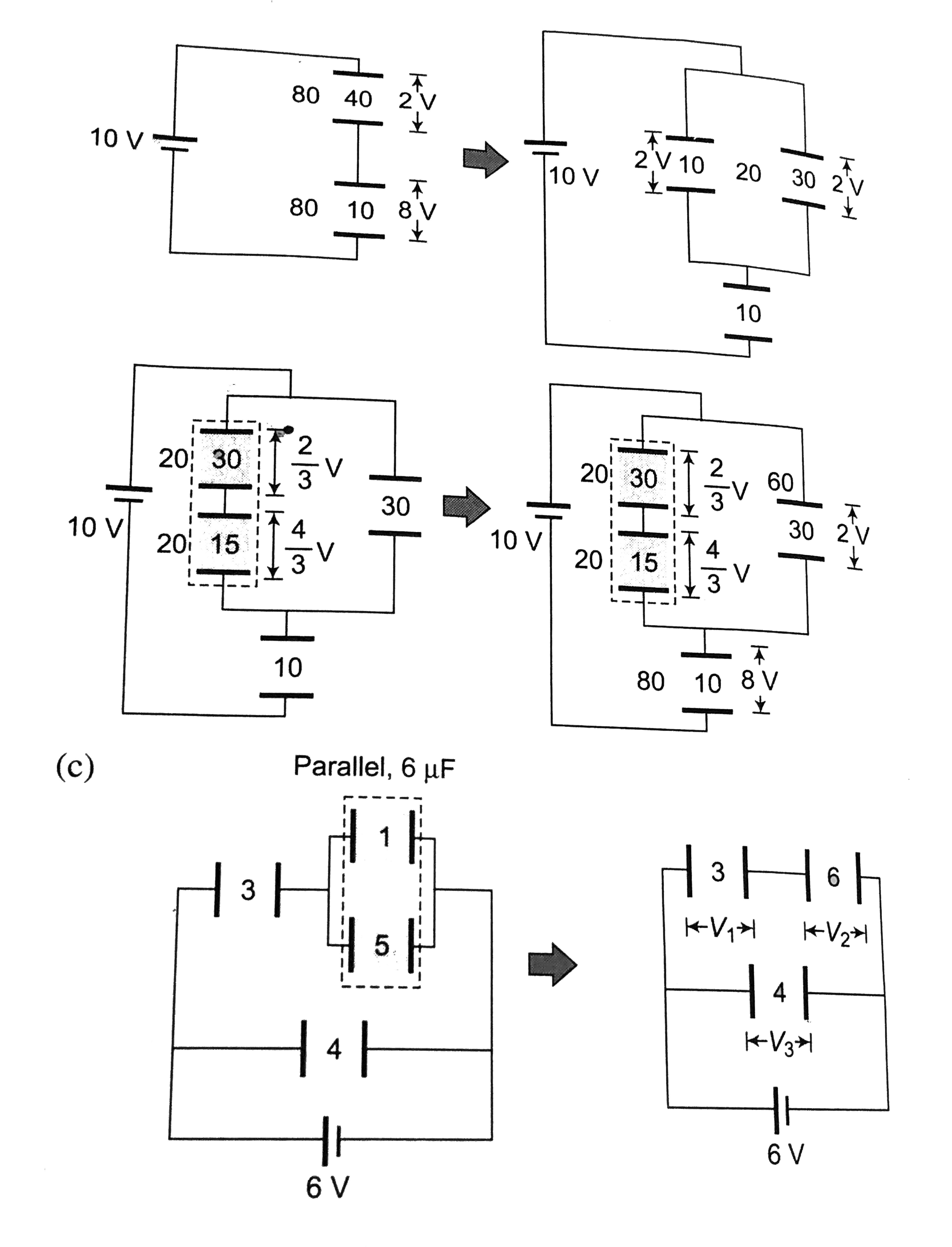
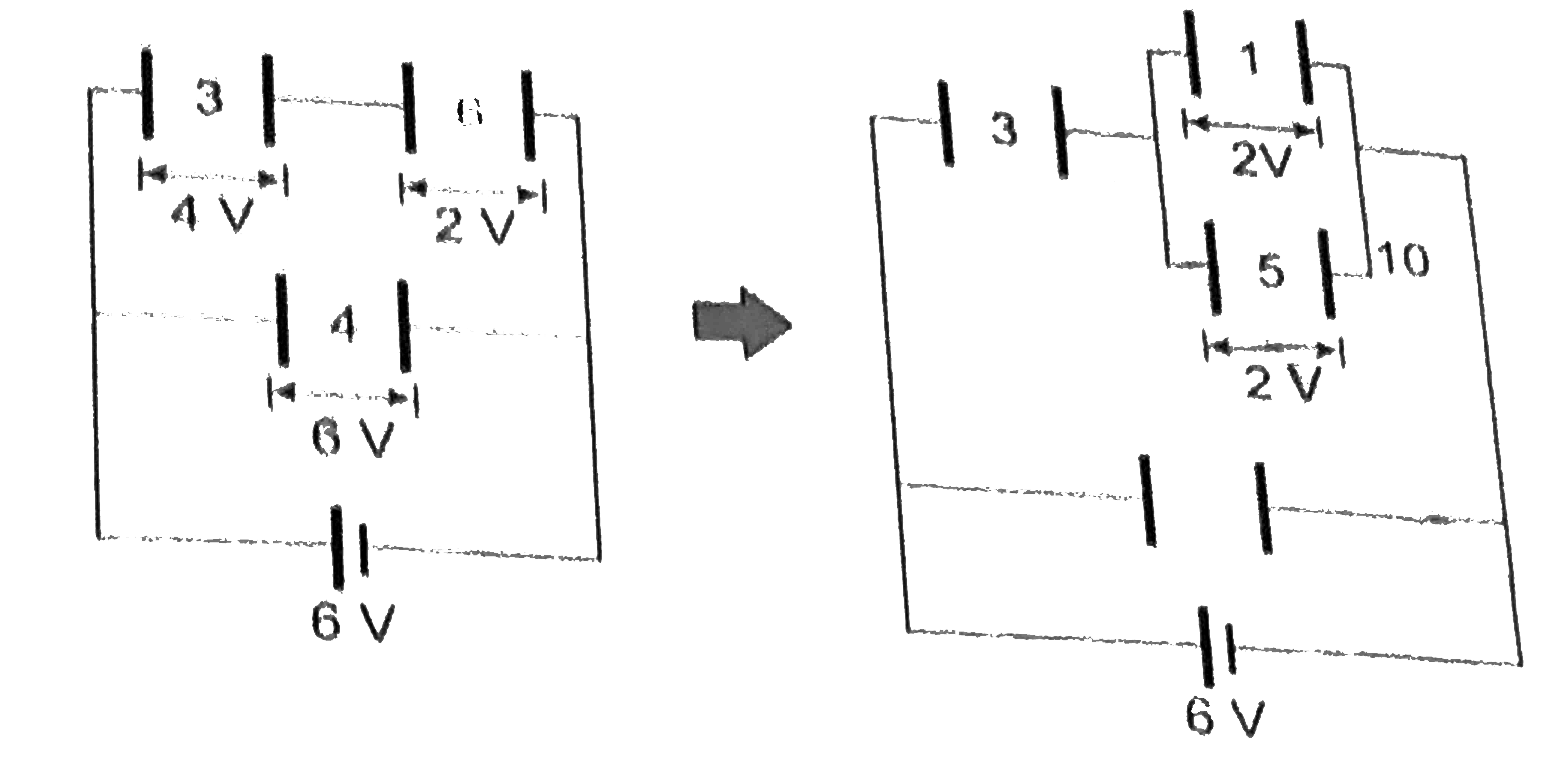
(c) 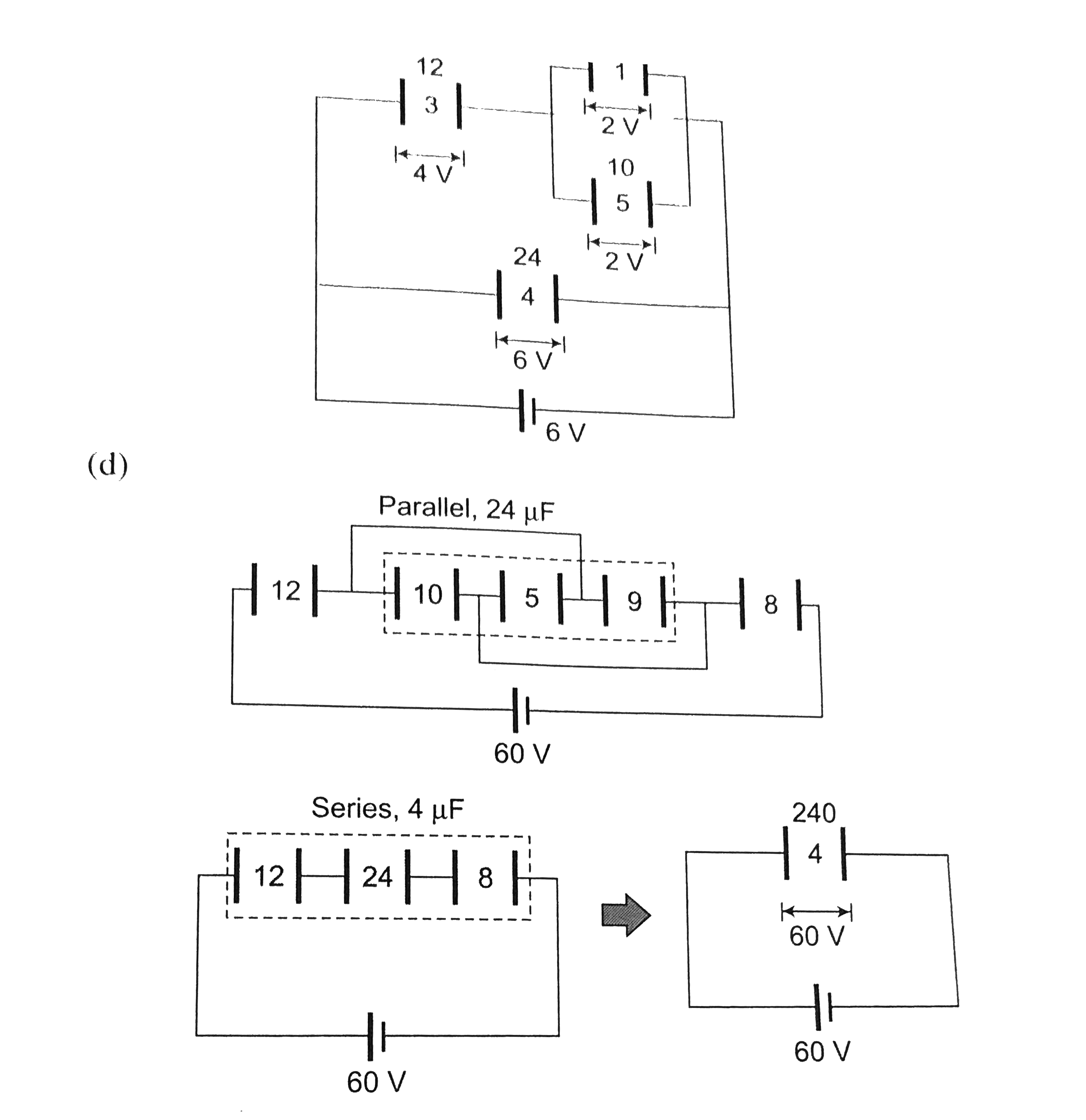
V1=(63+6)×6=4V,V2=6−V1=6−4=2V
V3=6V
Return to previous diagram.
Final diagram :
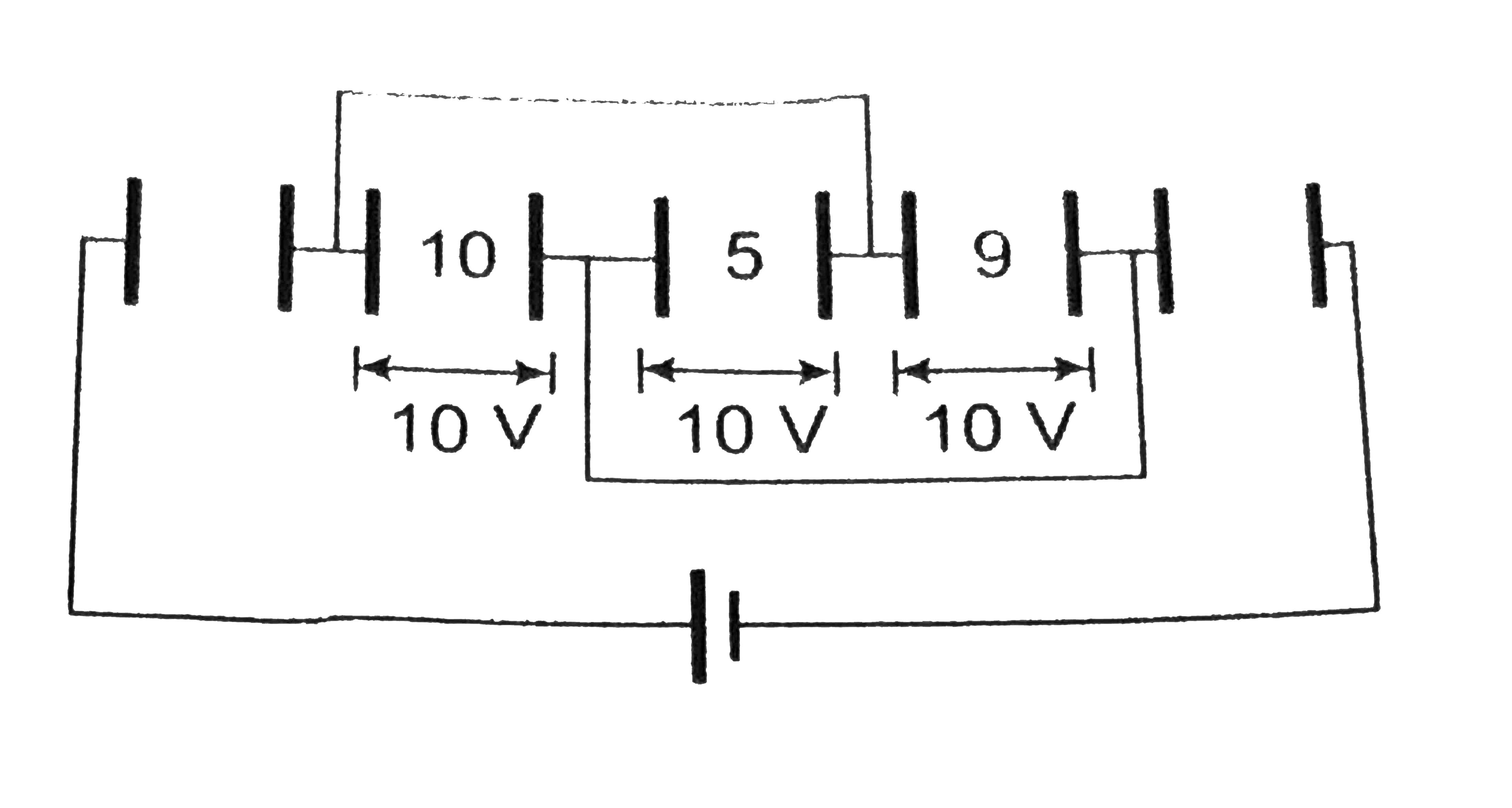
(d) 

Now, return to previous diagrams.

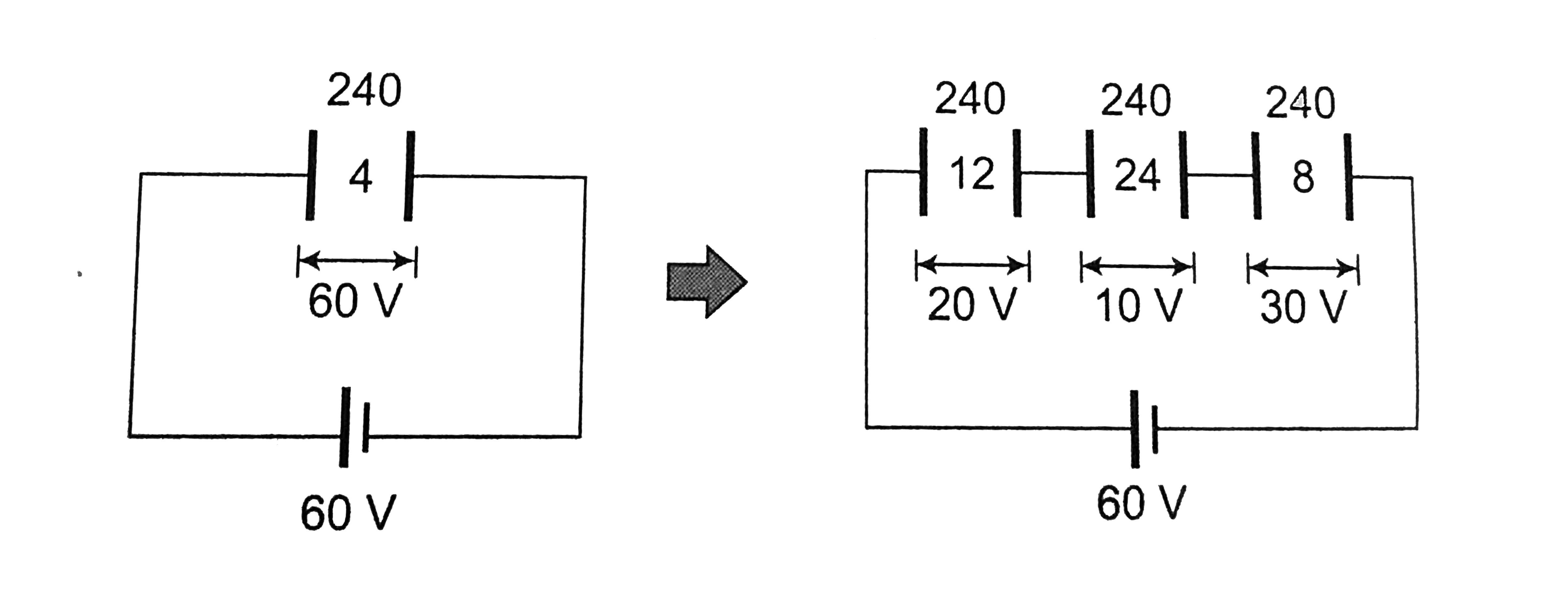
V1=24012=20V,V2=24024=10V,V32=2408=30V

Final diagram:

(e) 
V1=(2020+10)×30=20V
V2=30−V1=10V
Now, return to previous diagram.
Final diagram:
V1=2(2+163)x110=622×110=30V
V2=110−V1=80V
Now, return to previous diagram. Final diagram :
|
Topper's Solved these Questions
Similar Questions
Find charge on each capacitor.
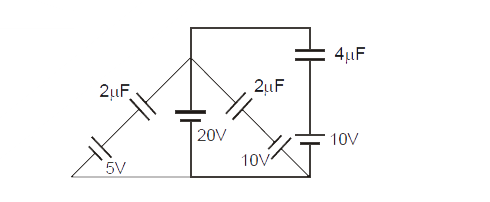
View SolutionFind charge on each capacitor.
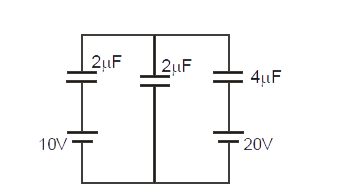
View SolutionFind charge on each capacitor

View SolutionFind the charged stored in all the capacitors
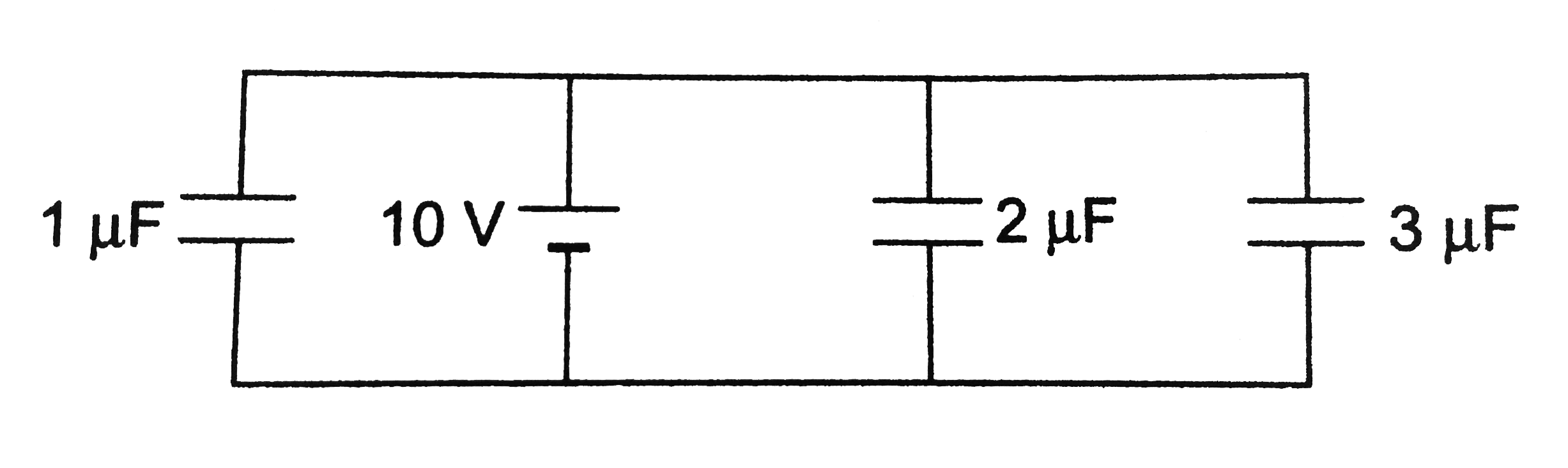
View SolutionFind the potential difference and caharge on each capacitences. All capacitance in μF.
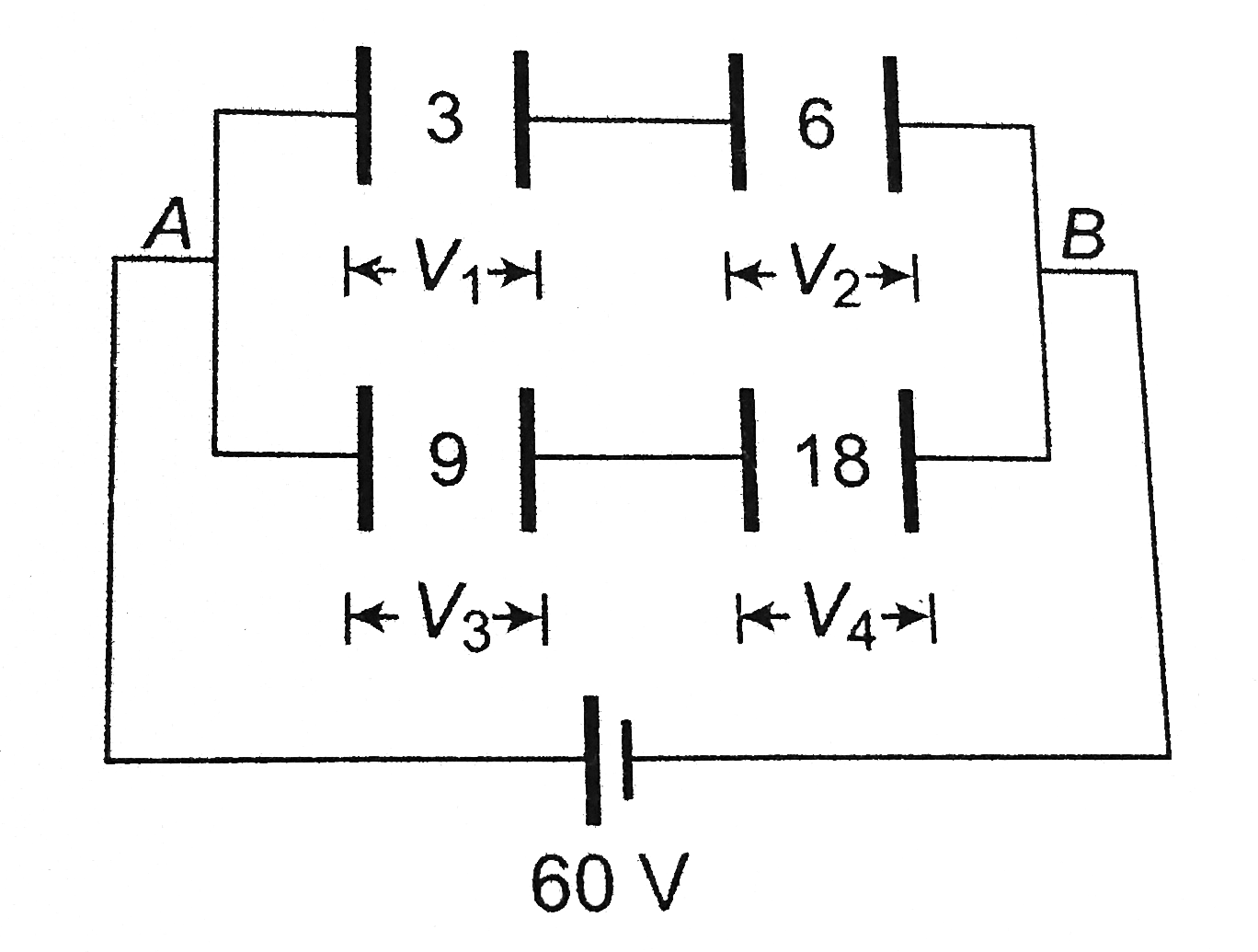
View SolutionFind charge in each capacitor:
View SolutionFind charge in each capacitor:
View SolutionFind the charges on 6μF and 4μF capacitors
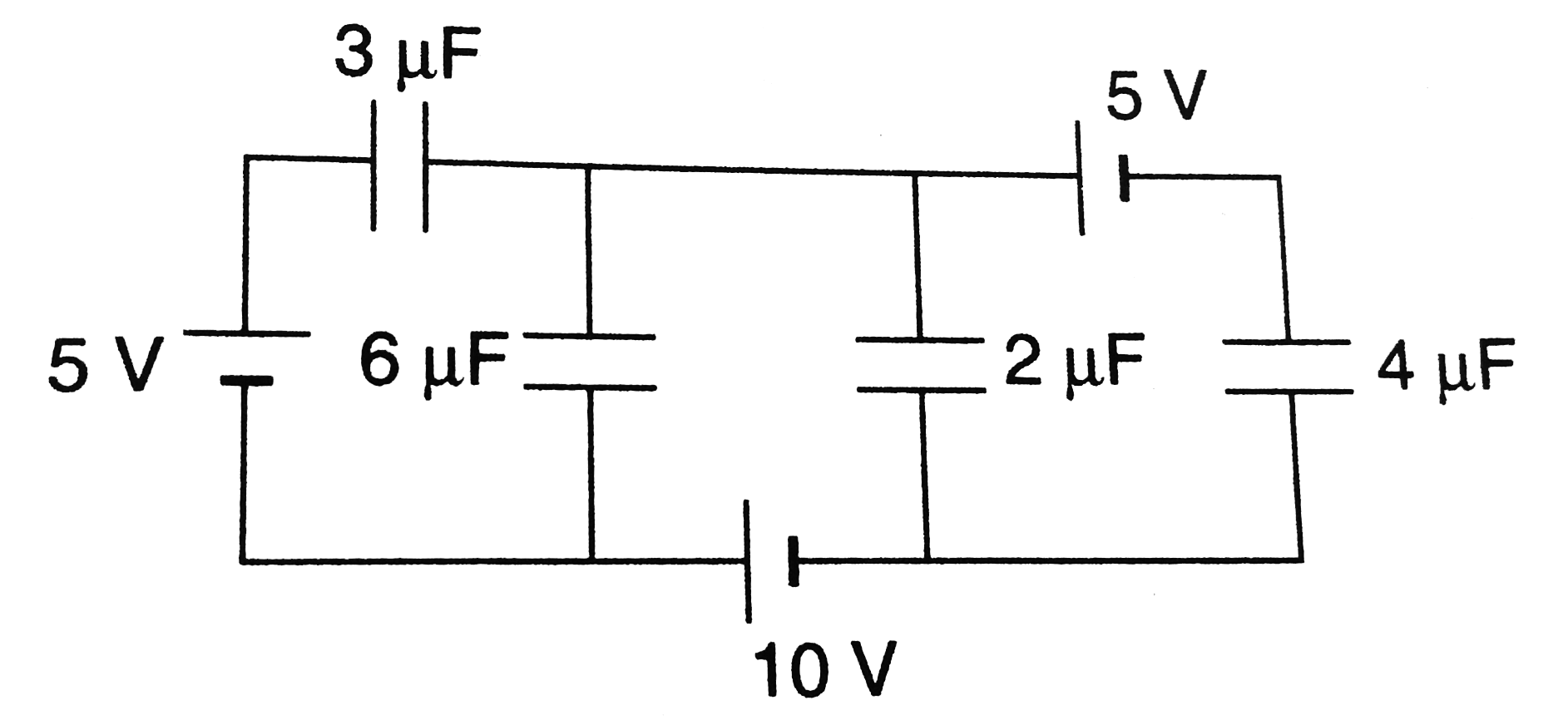
View SolutionA capacitor has capacitance 10μF audit is charged to a potential 150V. A second capacitor has a capacitance of 20μF and it is charged to a potential of 300V. After charging, the two capacitors are connected in parallel with their same polarity plates together by using wires of negligible capacitance. Find how much energy is dissipated?
View SolutionFind the potential difference and charge on each capacitor.
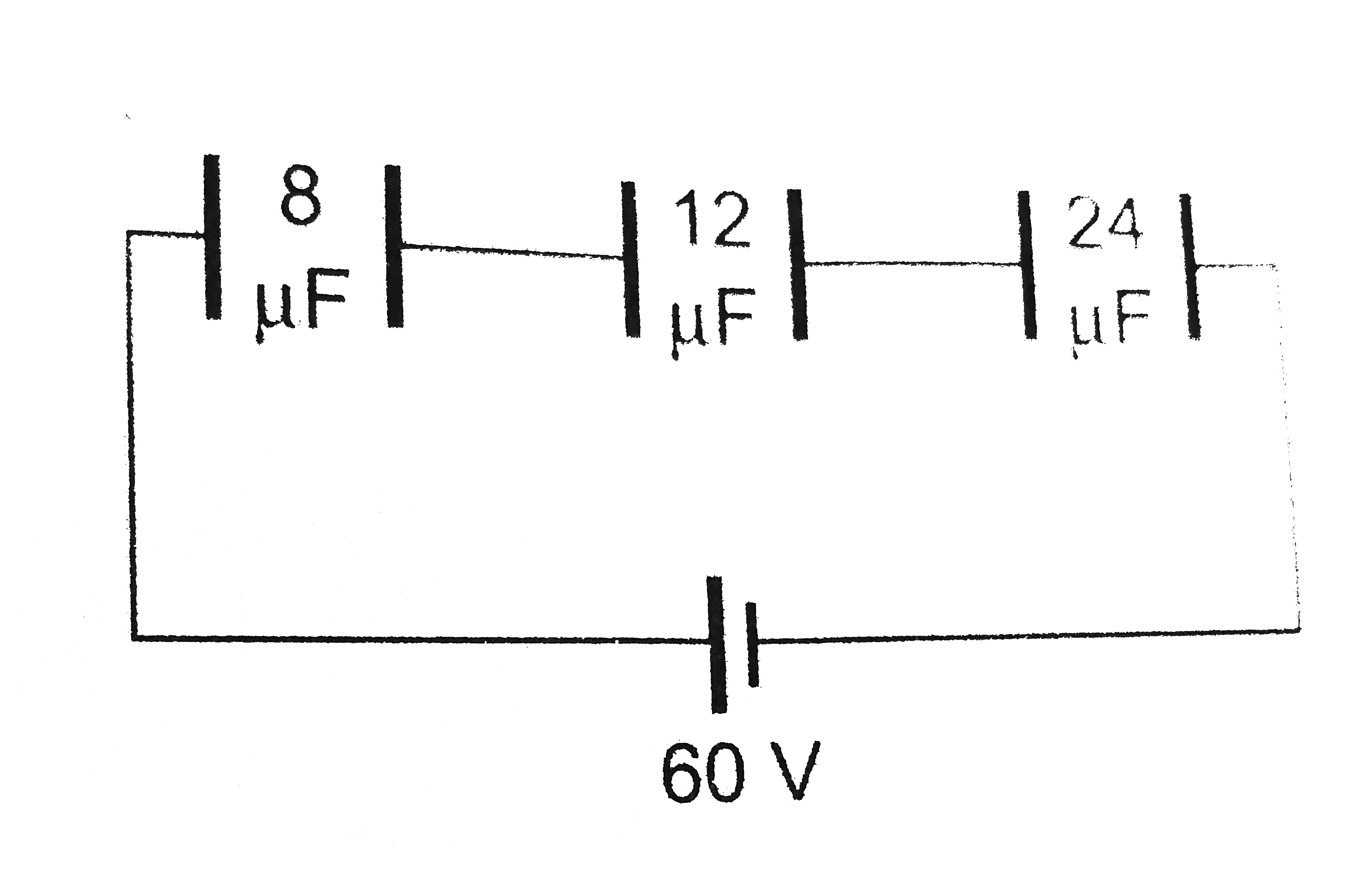
View Solution
