Two small conducting spheres each of mass 9×10−4kg are suspended from the same point by non conducting strings of length 100cm,They are given equal and similar charges until the strings are equally inclined at 45∘ each to the vertical,The charge on each spehre is ..........
1.4×10−6
1.6×10−6
2×10−6
1.96×10−6
The correct Answer is:1
To solve the problem, we need to find the charge on each of the two small conducting spheres that are suspended and inclined at 45 degrees from the vertical.
1. Understanding the Setup:
- We have two small conducting spheres, each with a mass m=9×10−4kg.
- They are suspended from the same point by non-conducting strings of length L=100cm=1m.
- The spheres are given equal and similar charges, and they are inclined at 45∘ to the vertical.
2. Free Body Diagram:
- Each sphere experiences three forces:
- The gravitational force mg acting downwards.
- The tension T in the string acting along the string.
- The electrostatic force F due to the repulsion between the two charged spheres.
3. Components of Forces:
- The tension T can be resolved into two components:
- Vertical component: Tcos(45∘)
- Horizontal component: Tsin(45∘)
4. Equilibrium in the Vertical Direction:
- In the vertical direction, the forces must balance:
Tcos(45∘)=mg
- Substituting cos(45∘)=1√2:
T⋅1√2=mg
- Therefore,
T=mg√2
5. Equilibrium in the Horizontal Direction:
- In the horizontal direction, the tension's horizontal component equals the electrostatic force:
Tsin(45∘)=F
- Substituting sin(45∘)=1√2:
T⋅1√2=F
6. Distance Between the Spheres:
- The distance R between the two spheres can be calculated using geometry:
R=2Lsin(45∘)=2L⋅1√2=√2L
- Substituting L=1m:
R=√2m
7. Electrostatic Force:
- The electrostatic force F between the two charges q is given by Coulomb's law:
F=kq2R2
- Substituting R=√2:
F=kq2(√2)2=kq22
8. Setting the Forces Equal:
- From the horizontal equilibrium, we can set the two expressions for F equal:
T⋅1√2=kq22
- Substituting T=mg√2:
mg√2⋅1√2=kq22
- Simplifying gives:
mg=kq22
9. Solving for Charge q:
- Rearranging gives:
q2=2mgk
- Substituting m=9×10−4kg, g=10m/s2, and k=9×109N m2/C2:
q2=2⋅(9×10−4)⋅109×109
- Simplifying gives:
q2=18×10−49×109=2×10−13
- Taking the square root:
q=√2×10−13=√2×10−7C≈1.414×10−7C
Final Answer:
The charge on each sphere is approximately 1.414×10−6C or 1.4×10−6C.
- We have two small conducting spheres, each with a mass m=9×10−4kg.
- They are suspended from the same point by non-conducting strings of length L=100cm=1m.
- The spheres are given equal and similar charges, and they are inclined at 45∘ to the vertical.
- Each sphere experiences three forces:
- The gravitational force mg acting downwards.
- The tension T in the string acting along the string.
- The electrostatic force F due to the repulsion between the two charged spheres.
- The tension T can be resolved into two components:
- Vertical component: Tcos(45∘)
- Horizontal component: Tsin(45∘)
- In the vertical direction, the forces must balance:
Tcos(45∘)=mg
- Substituting cos(45∘)=1√2:
T⋅1√2=mg
- Therefore,
T=mg√2
- In the horizontal direction, the tension's horizontal component equals the electrostatic force:
Tsin(45∘)=F
- Substituting sin(45∘)=1√2:
T⋅1√2=F
- The distance R between the two spheres can be calculated using geometry:
R=2Lsin(45∘)=2L⋅1√2=√2L
- Substituting L=1m:
R=√2m
- The electrostatic force F between the two charges q is given by Coulomb's law:
F=kq2R2
- Substituting R=√2:
F=kq2(√2)2=kq22
- From the horizontal equilibrium, we can set the two expressions for F equal:
T⋅1√2=kq22
- Substituting T=mg√2:
mg√2⋅1√2=kq22
- Simplifying gives:
mg=kq22
- Rearranging gives:
q2=2mgk
- Substituting m=9×10−4kg, g=10m/s2, and k=9×109N m2/C2:
q2=2⋅(9×10−4)⋅109×109
- Simplifying gives:
q2=18×10−49×109=2×10−13
- Taking the square root:
q=√2×10−13=√2×10−7C≈1.414×10−7C
The charge on each sphere is approximately 1.414×10−6C or 1.4×10−6C.
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level III (C.W)
55 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level 1
8 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level 1(C.W)
24 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - ADDITIONAL PROBLEMS
14 Videos
- EXPERIMENTAL PHYSICSBOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Comprehension type
6 Videos
Similar Questions
Two small spheres, each having a mass of 20 g, are suspended form a common point by two insulating strings of length 40 cm each. The spheres are identically charged and the speration between the balls at equilibrium is found to be 4 cm . Find the charge on each sphere.
View SolutionTwo pith ball of mass 0.5 each are suspended from a common point O by means of silk threads, each of length 20 cm. When the balls are given equal and similar charges, they repel each other so that the two threads make an angle of 60∘ with each-other. Determine the charge on each ball.
View Solution
Knowledge Check
Two small balls, each having equal positive charge Q are suspended by two insulationg strings of equal length l from a hook fixed to a stand. It mass of each ball =m and total angle between the two strings is 60∘m, then find the charge on each ball.
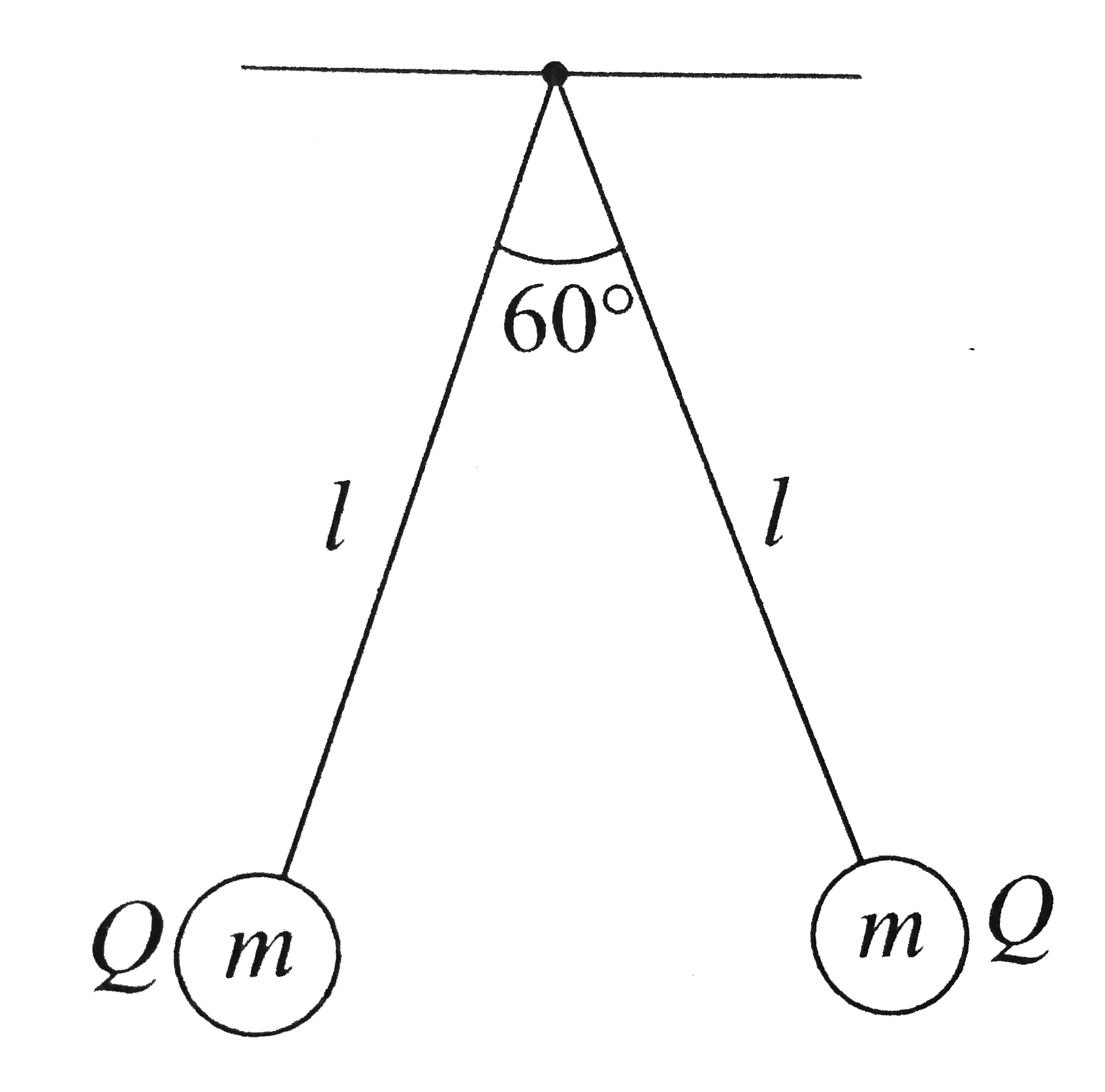 AL√√3mgkBL√mg√3kCL√mgkDL3√mgk
AL√√3mgkBL√mg√3kCL√mgkDL3√mgk
Two pith balls,, each weighting 10mg are suspended from the sam point by silk threads, each of length 0.25m. When equal and similar charges are placed on them they repel each other and are 10m apart. Find the charge on the each pith ball.
View SolutionTwo pith balls , of mass 10 mg, are suspended from the same point,each by a silk fibre 50 cm long . When equal and similar changes are given to them, they are repelled to a distance of 10 cm from each other. Calculate the chagre on either ball .
View SolutionTwo small spheres each of mass 10−6 kg are suspended from a point by silkk threads 50cm long. They are equally chareged and repel each other to a distance 20cm apart. Calculate charege on each Take g=9.8ms−2.
View SolutionThree identically charged, small spheres each of mass m are suspended from a common point by insulated light strings each of length I. The spheres are always on vertices of an equilateral triangle of length of the sides x(<<l). Calculate the rate dq/ dt with which charge on each sphere increases if length of the sides of the equilateral triangle increases slowly according to law dxdt=a√x
View SolutionThree paricles, each of mass m and carrying a charge q each, are suspended from a common pointby insulating massless strings each of length L. If the particles are in equilibrium and are located at the corners of an equilateral triangle of side a, calculate the charge q on each particle. Assume L>>a.
View SolutionTwo indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo small spheres each of mass m are suspended from a common point by threads 0.5 m long. They are equally charged and repel each other to a distance of 0.28m. If =g10ms−2, what is the charge on each sphere?
View Solution
