A half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
λ4εoln0
λ4π2ε0r
λ4πε0r
λ4πε0r2
The correct Answer is:1
To find the potential at the center of a half ring with radius r and linear charge density λ, we can follow these steps:
Step 1: Understanding the Charge Distribution
The half ring has a uniform linear charge density λ. This means that for a small segment of the half ring, the charge dq can be expressed in terms of the angle dθ as:
dq=λ⋅ds
where ds=rdθ is the length of the small segment at angle θ.
Step 2: Expressing the Charge Element
Substituting ds into the equation for dq:
dq=λ⋅(rdθ)
Step 3: Calculating the Potential Contribution from dq
The potential dV at the center of the half ring due to the small charge dq is given by the formula:
dV=kdqr
where k=14πϵ0 is Coulomb's constant. Substituting dq:
dV=k(λ⋅rdθ)r=kλdθ
Step 4: Integrating to Find Total Potential
To find the total potential V at the center, we need to integrate dV over the angle from −π2 to π2:
V=∫π2−π2dV=∫π2−π2kλdθ
This simplifies to:
V=kλ∫π2−π2dθ=kλ(θ)π2−π2=kλ(π2−(−π2))=kλ⋅π
Step 5: Final Expression for the Potential
Substituting k=14πϵ0:
V=14πϵ0⋅λ⋅π
This simplifies to:
V=λ4ϵ0
Conclusion
The potential at the center of the half ring is:
λ4ϵ0
The half ring has a uniform linear charge density λ. This means that for a small segment of the half ring, the charge dq can be expressed in terms of the angle dθ as:
dq=λ⋅ds
where ds=rdθ is the length of the small segment at angle θ.
Substituting ds into the equation for dq:
dq=λ⋅(rdθ)
The potential dV at the center of the half ring due to the small charge dq is given by the formula:
dV=kdqr
where k=14πϵ0 is Coulomb's constant. Substituting dq:
dV=k(λ⋅rdθ)r=kλdθ
To find the total potential V at the center, we need to integrate dV over the angle from −π2 to π2:
V=∫π2−π2dV=∫π2−π2kλdθ
This simplifies to:
V=kλ∫π2−π2dθ=kλ(θ)π2−π2=kλ(π2−(−π2))=kλ⋅π
Substituting k=14πϵ0:
V=14πϵ0⋅λ⋅π
This simplifies to:
V=λ4ϵ0
The potential at the center of the half ring is:
λ4ϵ0
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level 1
8 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level 2
10 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level II(C.W)
27 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - ADDITIONAL PROBLEMS
14 Videos
- EXPERIMENTAL PHYSICSBOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Comprehension type
6 Videos
Similar Questions
A quarter ring of radius R is having uniform charge density λ. Find the electric field and potential at the centre of the ring.
View SolutionA charge Q is distributed uniformly on a ring of radius R as shown in the following diagrams. Find the electric potential at the centre O of the ring

View Solution
Knowledge Check
A thin non-conducting ring of radius R has a linear charge density λ=λ0cosθ, where θ is measured as shown. The total electric dipole moment of the charge distribution is
 AR2λ0B2πR2λ0CπR2λ02DπR2λ0
AR2λ0B2πR2λ0CπR2λ02DπR2λ0A ring of radius R having a linear charge density λ moves towards a solid imaginary sphere of radius R2, so that the centre of ring passes through the centre of sphere. The axis of the ring is perpendicular to the line joining the centres of the ring and the sphere. The maximum flux through the sphere in this process is
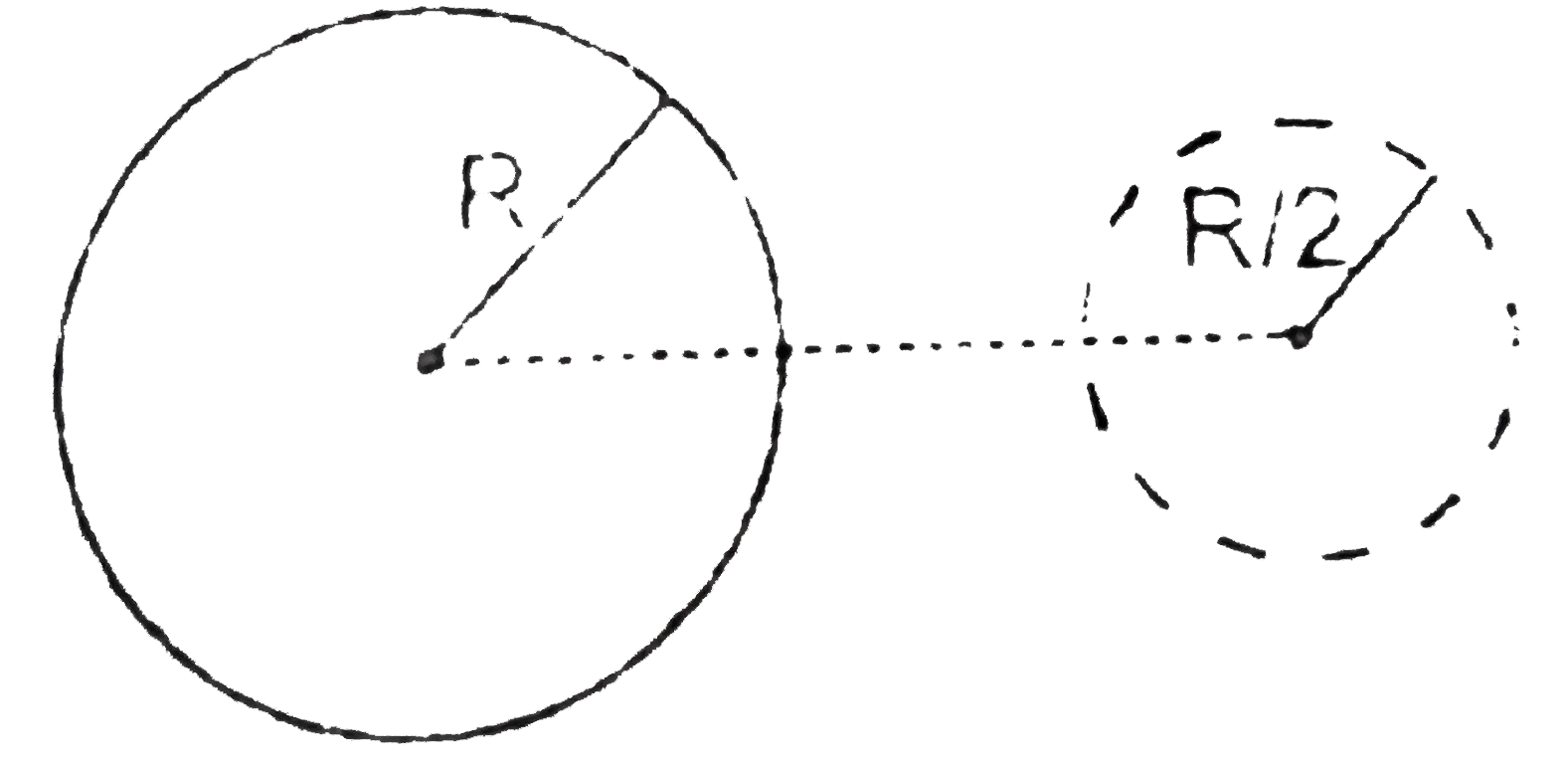 AλR∈0BλR2∈0CλπR4∈0DλπR3∈0
AλR∈0BλR2∈0CλπR4∈0DλπR3∈0
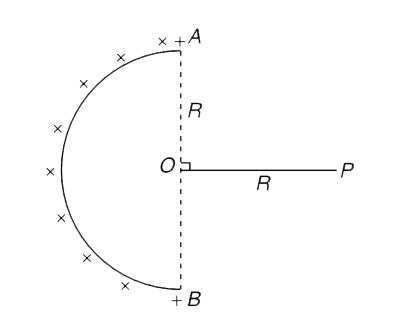
A sermicircular ring of radius R carries a uniform linear charge of λ. P is a point in the plane of the ring at a distance R from centre O. OP is perpendicular to AB. Find electric field intensity at point P.
View SolutionA charge +q is distributed over a thin ring of radius r with line charge density λ=qsin2θ/(πr). Note that the ring is in the x-y plane and θ is the angle made by →r with the x axis. The work done by the electric force in displacing a point charge +Q from the center of the ring to infinity is
View SolutionA thin nonconducting ring of radius r has a linear charge density q=q0cosθ, where q0 is a constant and θ is the angle at the centre from the diameter of maximum charge density in the anticlockwise direction. Find the electric field at the centre of the ring.
View SolutionA charge Q is distributed uniformly on a ring of radius R as shown in the following diagrams. Find the electric potential at the center O of the ring.
(a)
View SolutionFind the electric field due to an infinitely long cylindrical charge distribution of radius R and having linear charge density λ at a distance half of the radius from its axis.
View SolutionConsider a circular ring of radius r, uniformly charged with linear charge density λ. Find the electric potential aty a point on the exis at a distance x from the centre of the ring. Using this expression for the potential, find the electric field at this point.
View Solution
