Two electric dipoles each of dipolemoment p=6.2×10−30C−m are placed with their axis along the same line and their centres at a distanced =10−8cm.The force of attraction between dipole is
2.1×10−16N
2.1×10−12N
2.1×10−10N
2.1×10−8N
The correct Answer is:4
ui=0,uf=2×14πε0.e2(d/2)
ΔPE=KE=12mv2 calcualte v
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level 18videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level 210videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level II(C.W)27videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - ADDITIONAL PROBLEMS14videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Comprehension type6videos
EXPERIMENTAL PHYSICS
Similar Questions
Two electric dipoles , each of dipole moment p=6.2×10−30 C m are placed with their axes along the same line their centre a distance d=10−8 m apart . Calculate the force of attraction between the dipoles .
View SolutionTwo short electric dipoles of moment P and 8P are placed in opposite direction on a line at a distance of 15cm.The electric field will be zero at point between the dipoles whose distance from the dipole of moment P is?
View Solution
Knowledge Check
- Question 1 - Select One

Two point electric dipoles with dipole moment P1 and P2 are separated by a distance r with their dipole axes mutually perpendicular as shown. The force of interaction between the dipoles is (where k=14πε0)A2kP1P2r4B3kP1P2r3C4kP1P2r4D6kP1P2r4 - Question 2 - Select One
Two short dipoles , each of dipole moment P are placed at a large separation r. The force between them
Ais proportional to product of dipole momentaBis inversely proportional to r4Cthe force is attractive , if direction of dipole momenta are same , repulsive if oppositeDall options are correct - Question 3 - Select One
Two electric dipoles of moment p and 64p are placed in opposite direction on a line at a distance of 25cm. The electric field will be zero at point between the dipoles whose distance from the dipole of moment p is
A5cmB259cmC10cmD413cm
Calculate the magnitude of the force, due to an electric dipole of dipole moment 3.6×10−29C−m, on an electric 25mm from the center of the dipole , along the dipole axis. Assume that this distance is large relative to the dipole's charge separation.
View SolutionAn electric dipole of dipole moment 40×10−6C−m is enclosed by a closed surface. What is the net flux coming out of the surface?
View SolutionA short electric dipole has dipole moment of 4×10−9Cm. Determine the electric potential due to the dipole at a point distant 0.3 m from the centre of the dipole situated on (a) the axial line (b) on equatorial line and (c) on a line making an angle of 60∘ wth the dipole axis.
View SolutionA short electric dipole has dipole moment of 16 x 10^-9 C m. The electric potential due to dipole at a point at a distance of 0.6m from centre of dipole situated on aline making an angle of 60 degrees with dipole axis:
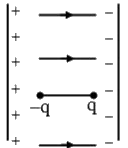
View SolutionAn electric dipole of dipole moment 2×10−10 coulomb is placed between parallel plate capacitor (see figure) having plate separation 2 cm and charged upto 100 V. Potential energy of the dipole will be -
 View Solution
View Solution

