A large sheet carries uniform surface charge density σ . A rod of length 2l has a linear charge density λ on one half and −λ on the second half. The rod is hinged at the midpoint O and makes an angle θ with the normal to the sheet. The torque experience by the rod is
σλl22ε0cosθ
σλl2ε0cos2θ
σλl22ε0sinθ
zero
The correct Answer is:C
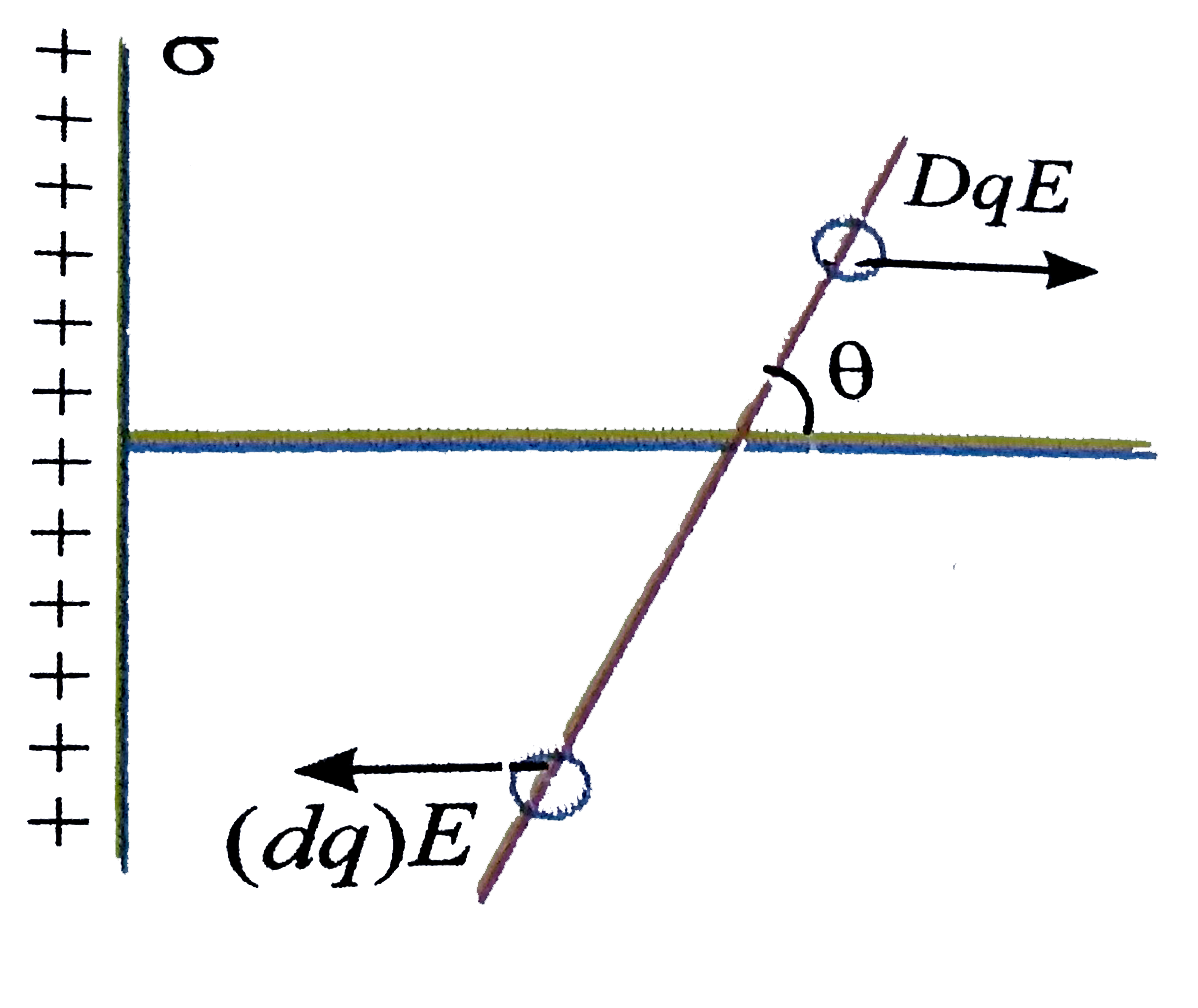
rArr By symmetry τ=σλl22ε0sinθ
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Passage I3videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Passage II3videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - NCERT based Question14videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - ADDITIONAL PROBLEMS14videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Comprehension type6videos
EXPERIMENTAL PHYSICS
Similar Questions
In the figure shown S is a large nonconducting sheet of uniform charge density σ. A rod R of length l and mass 'm' is parallel to the sheet and hinged at its mid point. The linear charge densities on the upper and lower half of the rod are shown in the figure. Find the angular acceleration of the rod just after it is released.
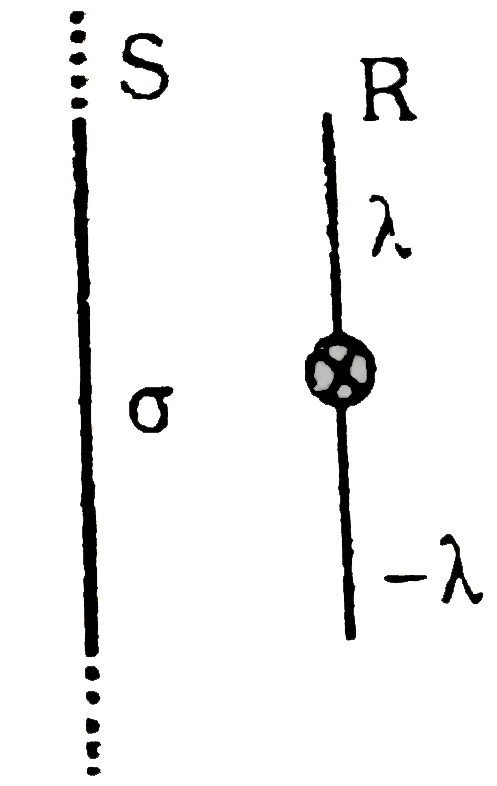 View Solution
View SolutionIn the figure shown, S is a large non-conducting sheet of uniform charge density σ. A rod R of length I and mass m is parallel to the sheet and hinged at its midpoint. The linear charge densities on the upper and lower half of the rod are shown in the figure. The angular acceleration of the rod just after it is released is pσλqmɛo. Find pq.
'(##CEN_KSR_PHY_JEE_C18_E01_031_Q16##)'View Solution
Knowledge Check
- Question 1 - Select One
A half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
Aλ4εoln0Bλ4π2ε0rCλ4πε0rDλ4πε0r2 - Question 2 - Select One
A ring carries a uniform linear charge density on one half and the linear charge density of same magnitude but opposite sign on the other half.
AThe component of electric field along the axis at all points on the axis is zeroBthe electric field along the axis and on the axis is zero only at the centreCthe resultant field at the centre is zeroDthe resultant field at all points on the axis is zero
In the figure shown S is a large nonconducting sheet of uniform charge density σ. A rod R of length l and mass 'm' is parallel to the sheet and hinged at its point. The linear charge densities on the upper and lower half of the rod are shown in the figure. Find the angular acceleration of the rod just after it is released
[3σλ2m∈0]
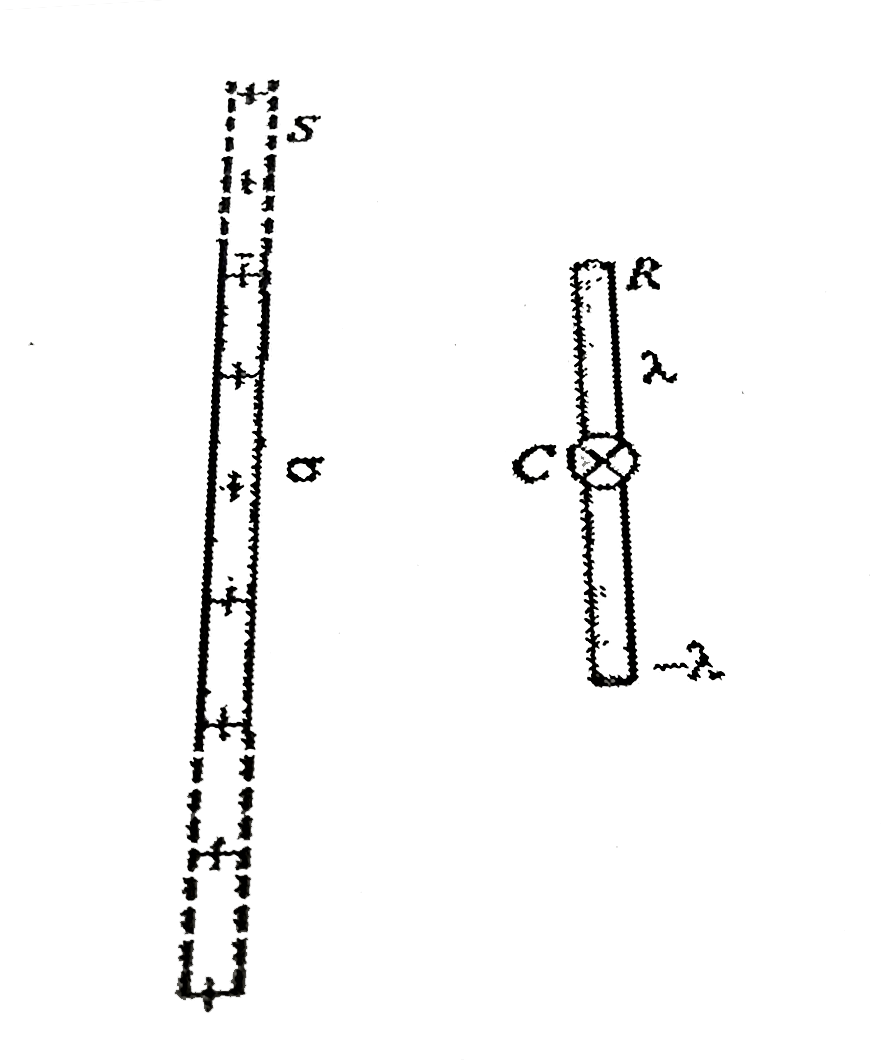 View Solution
View SolutionAn infinite thin non - conducting sheet has uniform surface charge density σ. Find the potential difference VA−VB between points A and B as shown in the figure. The line AB makes an angle of 37∘ with the normal to the sheet. (sin37∘=35)
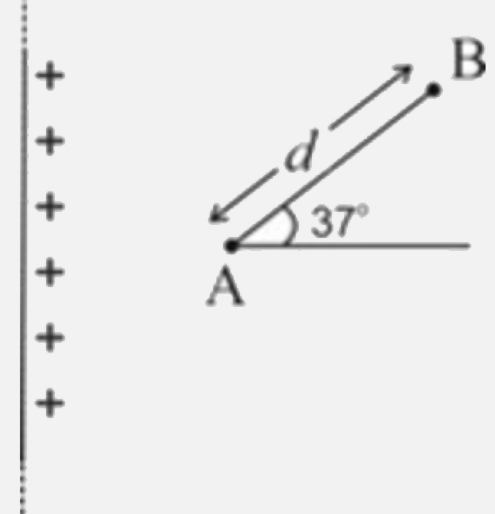 View Solution
View SolutionA uniform rod AB of mass m and length l is hinged at its mid point C. The left half (AC) of the rod has linear charge density −λ and the right half (CB) has +λ where λ is constant. A large non conducting sheet of uniform surface charge density σ is also present near the rod. Initially the rod is kept perpendicular to the sheet. The end A of the rod is initialy at a distance d. Now the rod is rotated by a small angle in the plane of the paper and released. Prove that the rod will perform SHM and find its time period.
 View Solution
View SolutionWhat is the electric field intensity at any point on the axis of a charged rod of length 'L' and linear charge density λ? The point is separated from the nearer end by a.
View SolutionYou are given a rod of length L. The linear mass density is λ such that λ=a+bx. Here a and b are constants and the mass of the rod increases as x decreases. Find the mass of the rod
 View Solution
View SolutionAn insulting thin rod of length l has a linear charge density ρ(x)=ρ0xl on it. The rod is rotated about an axis passing through the origin (x=0) and perpendicular to the rod. If the rod makes n rotations per second, then the time averaged magnetic moment of the rod is :
View Solution

