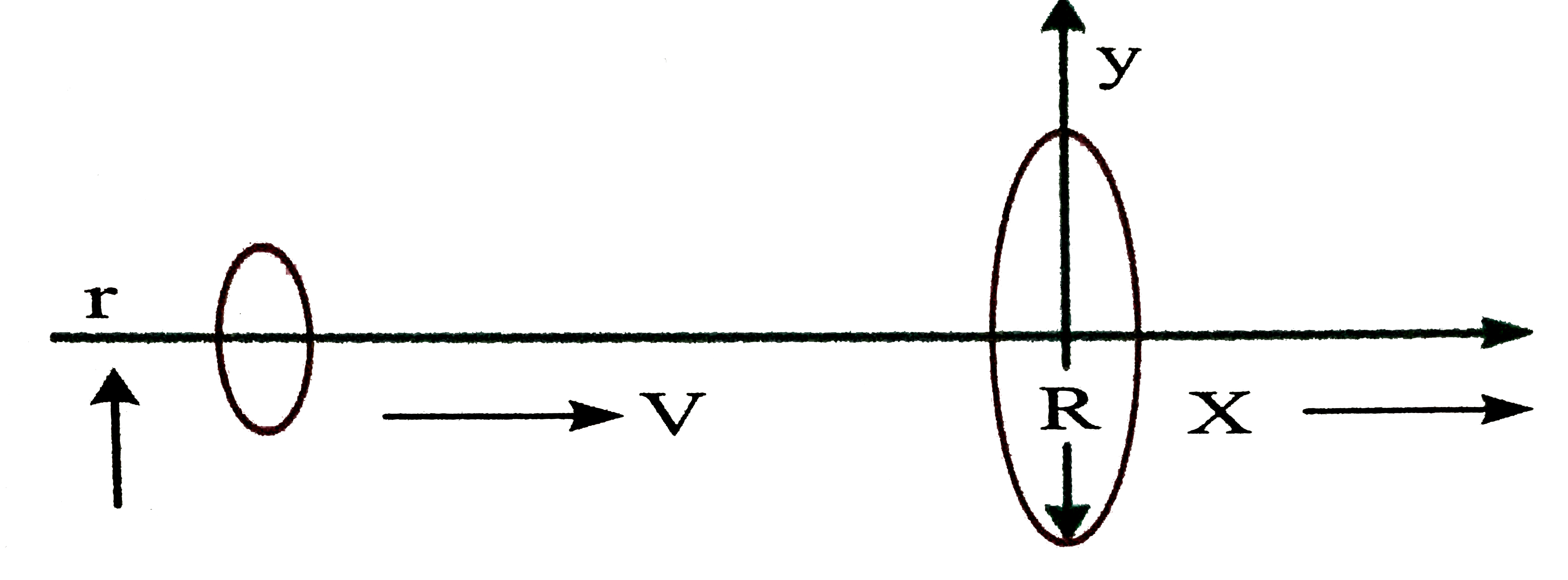
A ring of radius R is placed in the plane with its centre at origin and its axis along the x−aξs and having uniformly distributed positive charge.A ring of radius r(<<R) and coaxial with the larger ring is moving along the axis with constant velocity then the variation of electrical flux (ϕ) passing through the smaller ring with position will be best represented by :

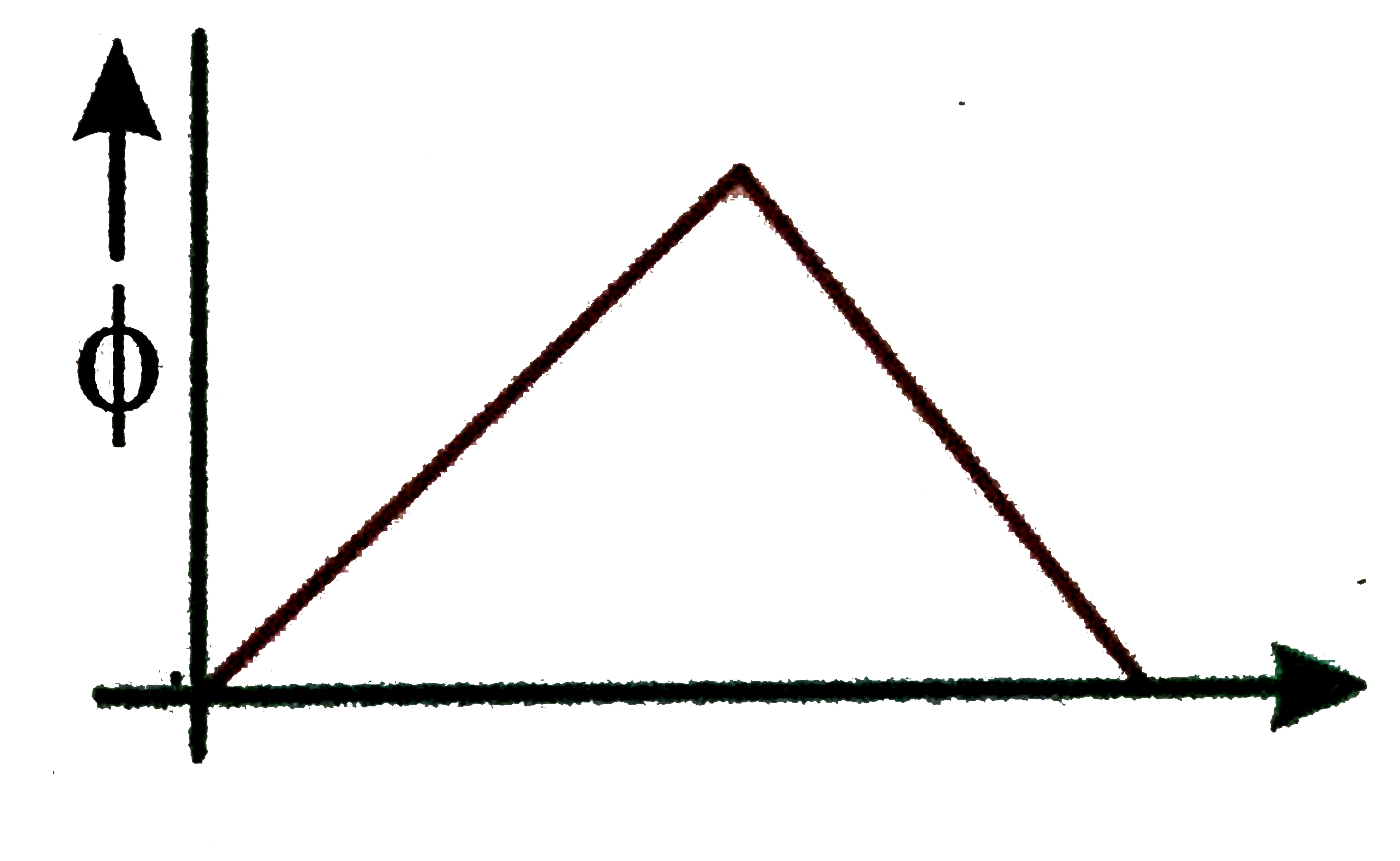

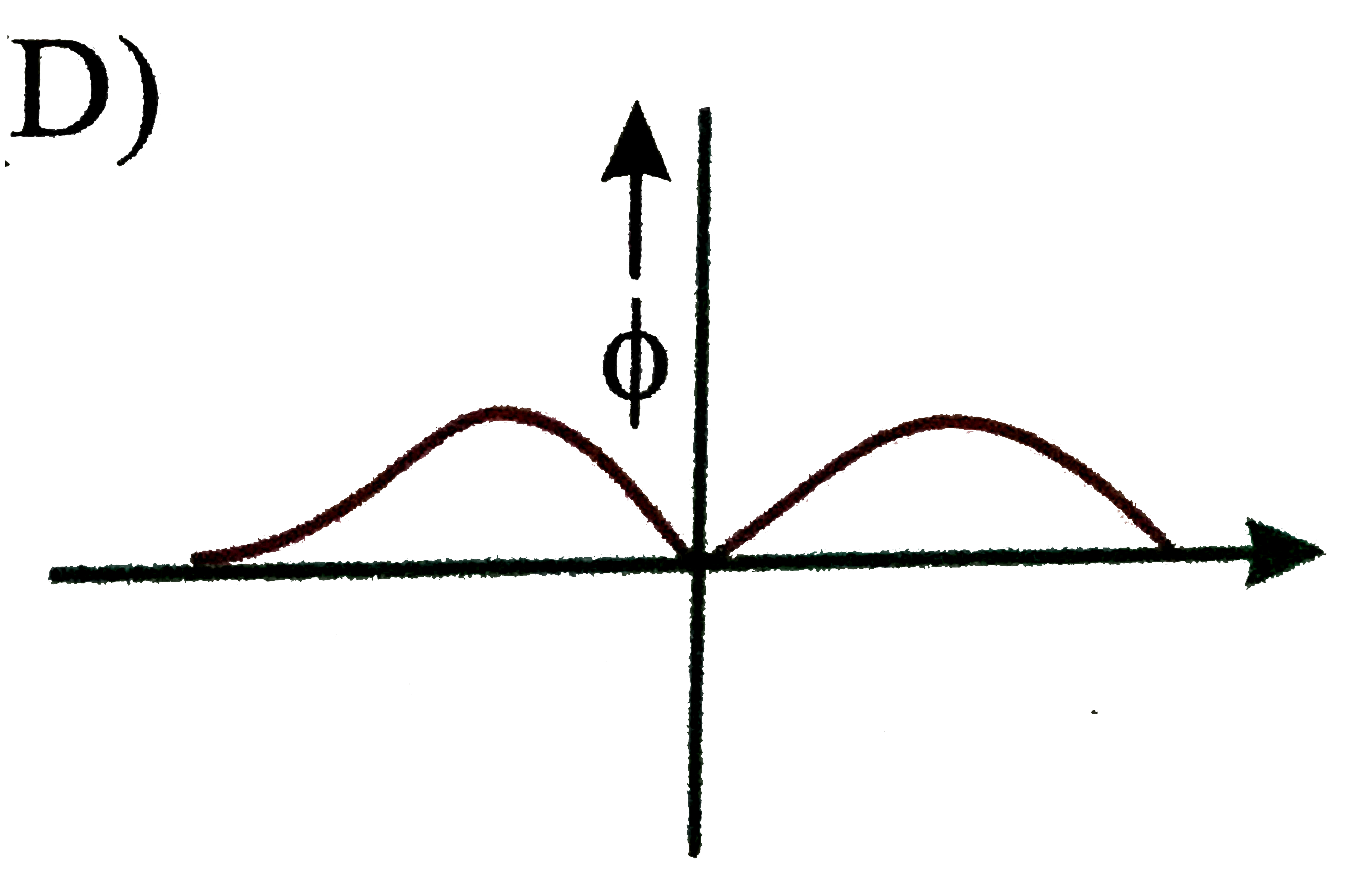
The correct Answer is:C
f=→E,→ds
since r<<R so we can consider electric field is constant throughout the surface of smaller ring.
hence f=E∝x(R2+x2)3/2
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Passage I3videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Passage II3videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - NCERT based Question14videos
ELECTROSTATICS AND GAUSS LAW
- BOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - ADDITIONAL PROBLEMS14videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Comprehension type6videos
EXPERIMENTAL PHYSICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A ring of radius R is placed in the plane its centre at origin and its axis along the x-axis and having uniformly distributed positive charge. A ring of radius r(<<R) and coaxial with the larger ring is moving along the axis with constant velocity , then the variation of electrical flux (ϕ) passing through the smaller ring with position will be best represent by :
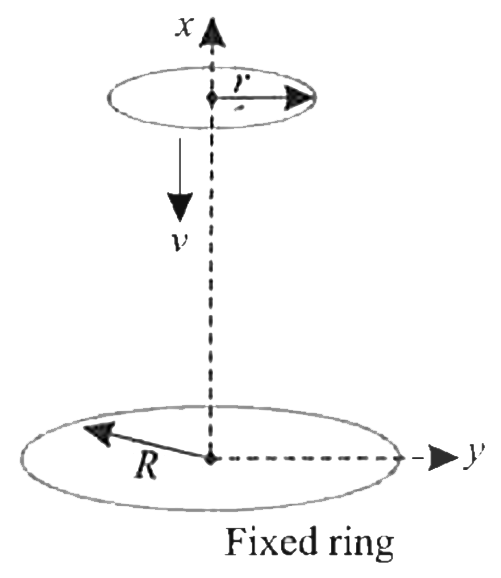 A
A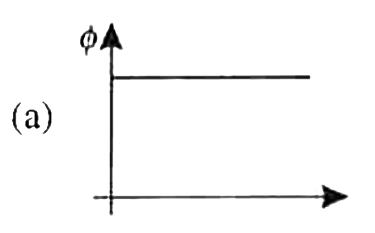 B
B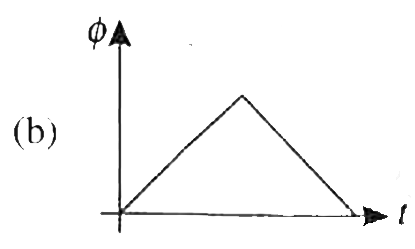 C
C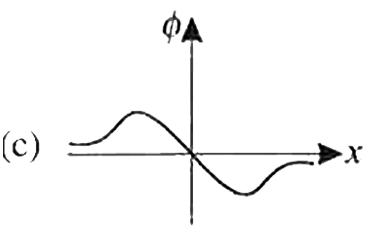 D
D
- Question 2 - Select One
A ring with a uniform charge Q and radius R, is placed in the yz plane with its centre at the origin
Athe field at the origin is zeroBThe potential at the origin is kQRCthe potential at the origin is kQx2Dthe filled at the point (x,0,0) is kQR2+x2 - Question 3 - Select One
Charges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
Aq2π2ε0R2Bq4π2ε0R2Cq4πε0R2Dq2πε0R2
A circular ring carries a uniformly distributed positive charge .The electric field(E) and potential (V) varies with distance (r ) from the centre of thr ring along its axis as
 View Solution
View SolutionA ring of radius R is charged uniformly with a charge +Q. The potential at a point on its axis at a distance 'r' from any point on ring will be-
View SolutionThe maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R will be
View SolutionA charge Q is uniformly distributed only on the fourths portion of a ring of radius R. The elctric potential at centre of ring is
View SolutionA non conduction ring of raducs R Has uniformly distributed positive charge Q.A small part of the ring of length d, is removed (d lt lt R) . The electric field at the centre of the ring now be .
View Solution

