A ring of radius R is charged uniformly with a charge +Q. The potential at a point on its axis at a distance 'r' from any point on ring will be-
kQ√R2+r2
kQr
kQ(r2+R2)3/2
kQr2(r2−R2)1/2
The correct Answer is:B
To find the electric potential at a point on the axis of a uniformly charged ring, we can follow these steps:
1. Understanding the Configuration:
- We have a ring of radius R uniformly charged with a total charge +Q.
- We want to find the electric potential at a point P located on the axis of the ring at a distance r from the center of the ring.
2. Identifying the Element of Charge:
- Consider a small element of charge dq on the ring. The total charge Q is uniformly distributed along the ring.
3. Calculating the Potential due to the Charge Element:
- The potential dV at point P due to the charge element dq is given by the formula:
dV=kdqd
where k is Coulomb's constant and d is the distance from the charge element dq to the point P.
4. Finding the Distance d:
- The distance d can be calculated using the Pythagorean theorem:
d=√R2+r2
where R is the radius of the ring and r is the distance from the center of the ring to point P.
5. Integrating to Find Total Potential:
- Since the potential due to each infinitesimal charge dq is the same at point P (due to symmetry), we can integrate over the entire ring:
V=∫dV=∫kdq√R2+r2
- The total charge Q can be expressed as:
Q=∫dq
- Therefore, the total potential V at point P becomes:
V=kQ√R2+r2
6. Final Result:
- The potential at point P on the axis of the ring is:
V=kQ√R2+r2
- We have a ring of radius R uniformly charged with a total charge +Q.
- We want to find the electric potential at a point P located on the axis of the ring at a distance r from the center of the ring.
- Consider a small element of charge dq on the ring. The total charge Q is uniformly distributed along the ring.
- The potential dV at point P due to the charge element dq is given by the formula:
dV=kdqd
where k is Coulomb's constant and d is the distance from the charge element dq to the point P.
- The distance d can be calculated using the Pythagorean theorem:
d=√R2+r2
where R is the radius of the ring and r is the distance from the center of the ring to point P.
- Since the potential due to each infinitesimal charge dq is the same at point P (due to symmetry), we can integrate over the entire ring:
V=∫dV=∫kdq√R2+r2
- The total charge Q can be expressed as:
Q=∫dq
- Therefore, the total potential V at point P becomes:
V=kQ√R2+r2
- The potential at point P on the axis of the ring is:
V=kQ√R2+r2
Topper's Solved these Questions
Similar Questions
Consider a circular ring of radius r, uniformly charged with linear charge density λ. Find the electric potential aty a point on the exis at a distance x from the centre of the ring. Using this expression for the potential, find the electric field at this point.
View SolutionA ring of radius R carries a uniformly distributed charge +Q. A point charge −q is placed on the axis of the ring at a distance 2R from the centre of the ring and released from rest. The particle executes a ismple harmonic motion along the axis of the ring.
View Solution
Knowledge Check
A sphere of radius R, is charged uniformly with total charge Q. Then correct statement for electric field is (r = distance from centre): -
AKQrR3, where r<RBKQr2, where r≥RCit is zero, at all pointsD(A) and (B) bothWhich statement is true :-
(i) A ring of radius R carries a uniformly distributed charge +Q. A point charge -q is placed on the axis of the ring at a distance 2R from the centre of the ring and released from rest. The particle executes a smiple harmonic motion along the axis of the ring.
(ii) Electrons move from a region of higher potential to that of lower potentialAonly (i)Bonly (ii)C(i), (ii)Dnone of themA ring of radius R carries a charge +q. A test charge −q0 is released on its axis at a distance √3R from its centre. How much kinetic energy will be acquired by the test charge when it reaches at the centre of the ring ?
A14πε0(qq0R)B14πε0(qq02R)C14πε0(qq0√3R)D14πε0(qq03R)
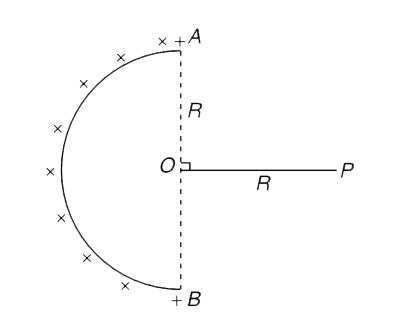
A sermicircular ring of radius R carries a uniform linear charge of λ. P is a point in the plane of the ring at a distance R from centre O. OP is perpendicular to AB. Find electric field intensity at point P.
View SolutionTwo co-axisal rings, each of radius R, are separated by a small distance l(ltltR) and carry charges q and -q.Find the electric potential and field at a point on the axis at a distance x from the midpoint between the rings,
View SolutionA ring has radius 30cm and a charge of 2nC .The electric potential on the axis of the ring at a distance of 40cm from its centre will be
View SolutionA thin wire ring of radius R carries a charge q. The ring si oriented parallel to an infinite conducting plane and is spearated by a distance l from it. Find :
(a) the surface chagre density at that point fo the plane symmetrical with respect to the ring,
(b) the strength and the potential of the electric field at the centre of the ring.
View SolutionAn unchanged conducting sphere of radius R is placed near a uniformly charge ring of radius R. Total charge on ring is Q. The centre of sphere lies on axis of ring and distance of centre of sphere from centre of ring is R

View Solution
