A proton is projected with a velocity 107ms−1, at right angles to a uniform magnetic field of induction 100mT. The time ( in second ) taken by the proton to traverse 90∘ are is :( Mass of proton =1.65×10−27kg an charge of proton =1.6×10−19C)

A

0.81×10−7

B

1.62×10−7

C

2.43×10−7

D

3.24×10−7

Video Solution
Doubtnut Promotions Banner
Text Solution
Generated By DoubtnutGPT

The correct Answer is:2

To solve the problem, we need to find the time taken by a proton to traverse a 90-degree arc in a magnetic field. Here's a step-by-step solution:

Step 1: Understand the motion of the proton in the magnetic field
When a charged particle like a proton moves perpendicular to a magnetic field, it follows a circular path. The radius of this circular path can be calculated using the formula:

r=mvqB

where:
- m = mass of the proton = 1.65×10−27kg
- v = velocity of the proton = 107m/s
- q = charge of the proton = 1.6×10−19C
- B = magnetic field induction = 100mT=100×10−3T

Step 2: Calculate the radius r
Substituting the values into the formula for the radius:

r=(1.65×10−27kg)(107m/s)(1.6×10−19C)(100×10−3T)

Calculating the denominator:

(1.6×10−19)(100×10−3)=1.6×10−19×10−1=1.6×10−20

Now calculating the radius:

r=(1.65×10−27)(107)1.6×10−20=1.65×10−201.6×10−20≈1.03125m

Step 3: Calculate the arc length for 90 degrees
The arc length s for a 90-degree angle (which is π2 radians) can be calculated as:

s=π2×r

Substituting the radius we calculated:

s=π2×1.03125≈1.62m

Step 4: Calculate the time taken to traverse the arc
The time t taken to traverse the arc can be calculated using the formula:

t=sv

Substituting the values:

t=1.62107=1.62×10−7s

Final Answer
The time taken by the proton to traverse 90 degrees is approximately:

t≈1.62×10−7s

Updated on:7/8/2024
|
Class 12PHYSICSMOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A proton is moving perpendicular to a uniform magnetic field of 2.5 tesla with 2 MeV kinetic energy. The force on proton is _______N. (Mass of proton= 1.6×10−27 kg, charge of proton =1.6×10−19 C)

    A8×10−12
    B8×10−11
    C3×10−11
    D3×10−10

  • The figure shows a region of length ‘l’ with a uniform magnetic field of 0.3 T in it and a proton entering the region with velocity 4×105 ms−1 making an angle 60∘ with the field. If the proton completes 10 revolution by the time it cross the region shown, ‘l’ is close to (mass of proton =1.67×1027 kg , charge of the proton =1.6×10−19 C )
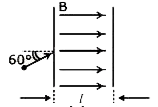    ocr_image

    A0.11 m
    B0.22m
    C0.44m
    D0.88m

  • The maximum kinetic energy of protons in a cyclotron of radius 0.4 m in a magnetic field of 0.5 T is (mass of proton = 1.67×10−27 kg, charge of proton =1.6×10−19 C)

    A3 MeV
    B1.9 MeV
    C5 MeV
    D4 MeV