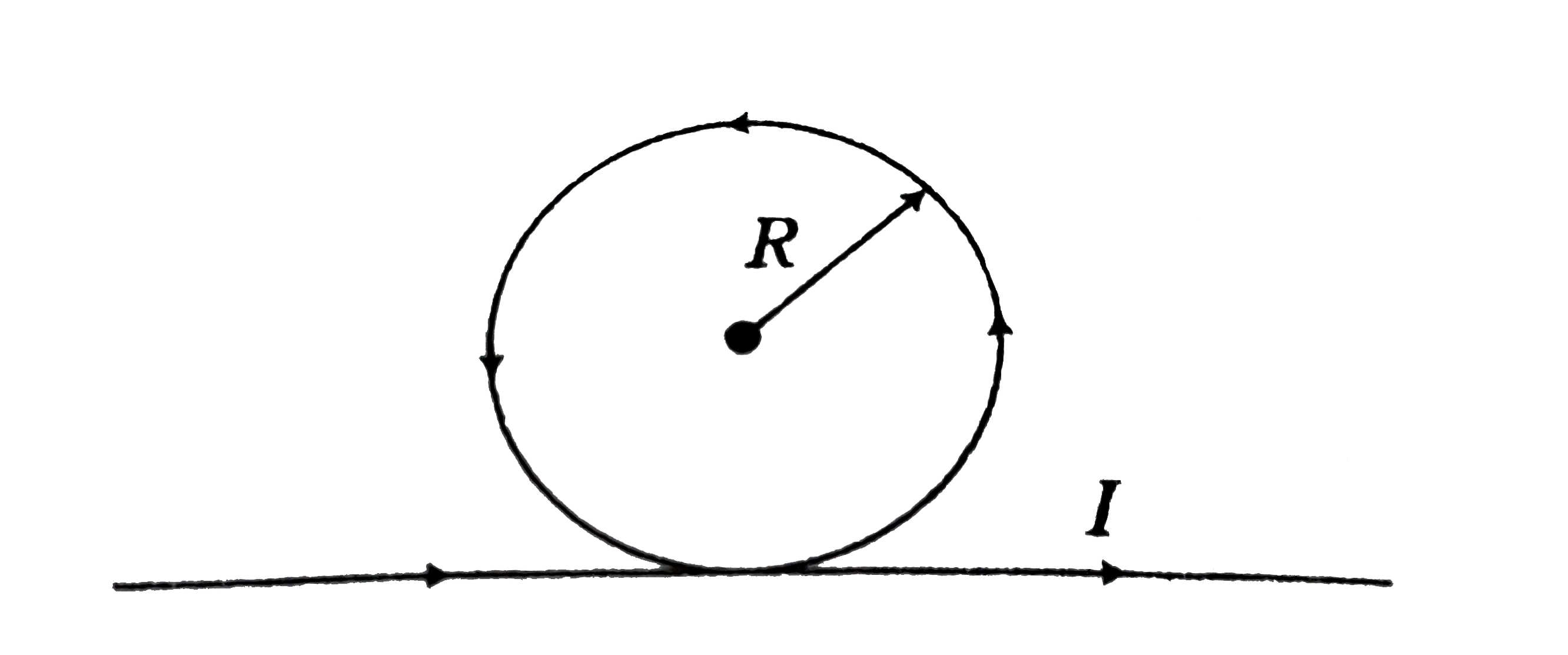
Two long straight wires are connected by a circular section which has a radius R. All the three segments lie in the same plane and carry a current I. The magnetic induction at the centre O of the circular segments is

μ0I4πR
αμ0I4πR
αμ0IR
αμ0I2πR
The correct Answer is:2
B=μ0IR×θ4∏
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - LEVEL-III
45 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT Based Questions
20 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - LEVEL-I(C.W)
58 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)
9 Videos
Similar Questions
Two identical wires each of length L are bent to form a circular loop and a square loop. If the same current i flows in the two wires, then the ratio of the magnetic inductions at the centre of the circular and square loops is :
View SolutionAn infinitely long straight conductor is bent into the shape as shown in the figure. It carries a current of i ampere and the radius of the circular loop is V metre. The magnetic induction at the centre of the circular part is-

View Solution
Knowledge Check
A long current wire is bent in the shapes shown in figure. The circular portion has radius R. The magnetic induction at the center of the circular segment is
 A−μ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],−μ0I4πR[ˆk+ˆj+3π2ˆi]Bμ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]C−μ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]Dμ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]
A−μ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],−μ0I4πR[ˆk+ˆj+3π2ˆi]Bμ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]C−μ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]Dμ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]The magnetic induction at the centre of a current carrying circular of coil radius r, is
ADirectly proportional to rBInversely proportional rCDirectly proportional to rDInversely proportional to r
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius RAμ0l2R(1+3ππ)Bμ0l4R(1+3ππ)Cμ0l8R(1+3ππ)Dμ0l8R(2+3ππ)
An infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R metre. The magnetic induction at the centre of loop is
View SolutionThe magnetic induction at any point due to a long straight wire carrying a current is
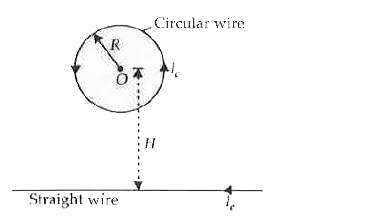
View SolutionCircular loop of a wire and a long straight wire carry currents and respectively as shown in figure. Assuming that these are placed in the same plane, the magnetic fields will be zero at the centre of the loop when separation H Circular wire Straight wire
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

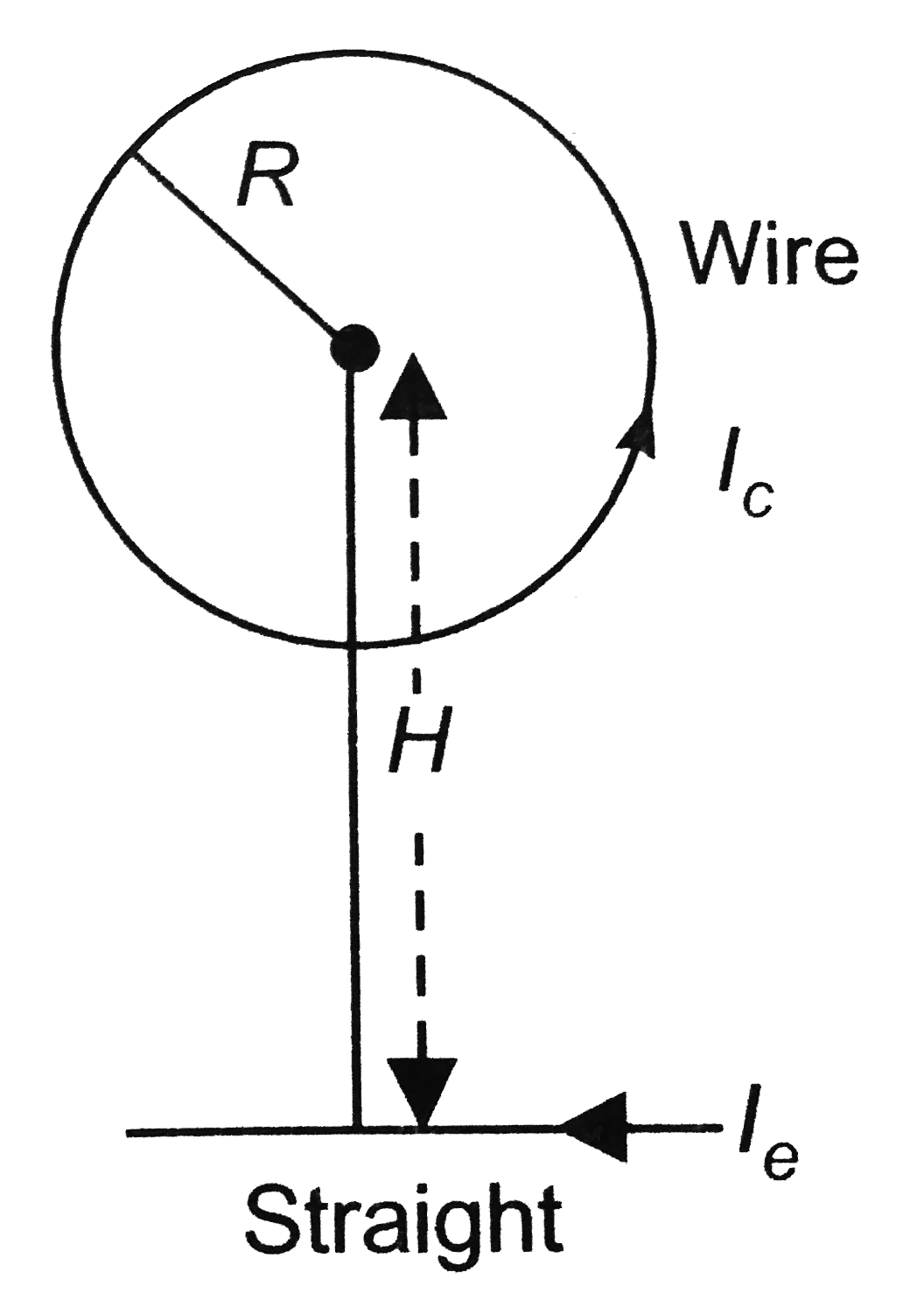
View SolutionCircular loop of a wire and a long straight wire carry current Ic and Ierespectively as shown in figure. Assuming that these are placed in the same plane. The magnetic field will be zero at the centre of the loop when the separation H is:
View Solution
