Q charge is uniformaly distributed over the same surface of a right circular cone of semi -vertical angle theta and height h The cone is uniformly rotated about its axis at angular velocity omega Calculated associated magnetic dipole moment
 .
.
Qωtan2θh24ˆn
Qωtan2θh22ˆn
Qωtan2θh23ˆn
Qωtan2θh2ˆn
The correct Answer is:A
Surface area of the cone =πh2tanθsecθ hence , charge per unit surface area
=Qπh2tanθsecθ
=Qπh2tanθsecθ(2π)(xtanθ)dx(cosθ)(2Qh2)xdx
The current dl due to the rotation this charge is given by

dl=(ω2π)(2Qh2)xdx
Hence, the magnetic moment (dμ) associated with this current would be.
d→μ=(Qω9πh2)(x)(π)(xthanθ)2(dx)ˆn
=(Qωtan2θ)h2x3dxˆn
(ˆn= unit vector along the axis )
→μ=(Qωtan2θh2)(∫h0x3dx)ˆn
=Qωtan2θh24ˆn
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - LEVEL-VI (SINGLE ANSWER QUESTION)81videos
MOVING CHARGES AND MAGNETISM
- BOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Level =I (H.W)42videos
MOVING CHARGES AND MAGNETISM
- BOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT Based Questions20videos
MOVING CHARGES AND MAGNETISM
- BOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)17videos
MAGNETISM AND MATTER
- BOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)9videos
NUCLEAR PHYSICS
Similar Questions
A ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(iii)Magnetic moment of ring.View SolutionA uniform charged disc whose total charge has magnitude q and whose radius is r rotates with constant angular velocity of magnitude ω. What is the magnetic dipole moment?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If the lateral surface of right circular cone is 2 times its base , then the semi-vertical angle of the cone must be :
A15∘B30∘C45∘D60∘ - Question 2 - Select One
If the lateral surface of right circular cone is 2 times its base , then the semi-vertical angle of the cone must be :
A15∘B30∘C45∘D60∘
A uniformly charged thin conducting spherical shell of radius R and charge q is rotated with constant angular velocity ω about a diameter. The magnetic dipole moment of the system is
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(ii) Magnetic field produced at the centre of ring.View SolutionA thin uniformring of radius R carrying uniform charge Q and mass M rotates about its axis with angular velocity ω. The ratio of its magnetic moment and angular momentum is:
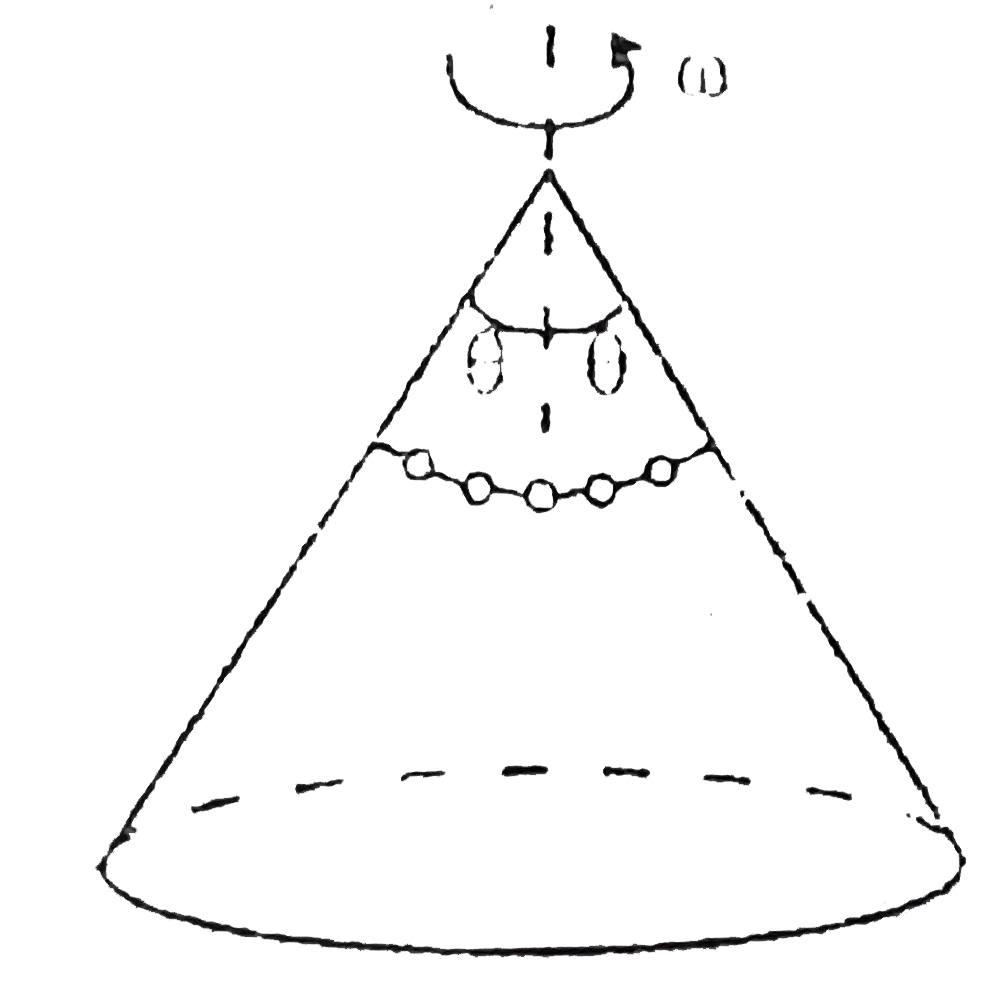
View SolutionA chain of mass 'm' and radius 'r' is placed onto a cone of semi vertical angle θ. Cone rotated with angular velocity ω. Find the tension in the chain if it does not slide on the cone.
 View Solution
View SolutionA rod has a total charge Q uniformly distributed along its length L. If the rod rotates with angular velocity ω about its end, compute its magnetic moment.
 View Solution
View SolutionA liquid has been poured into a cylindrical vessel. What shape will the surface of the liquid have if the vessel is rotated uniformly about its axis with an angular velocity ω ?
View Solution

