A chain of mass 'm' and radius 'r' is placed onto a cone of semi vertical angle $θ$ . Cone rotated with angular velocity $ω$ . Find the tension in the chain if it does not slide on the cone.

Video Solution

Text Solution

Verified by Experts

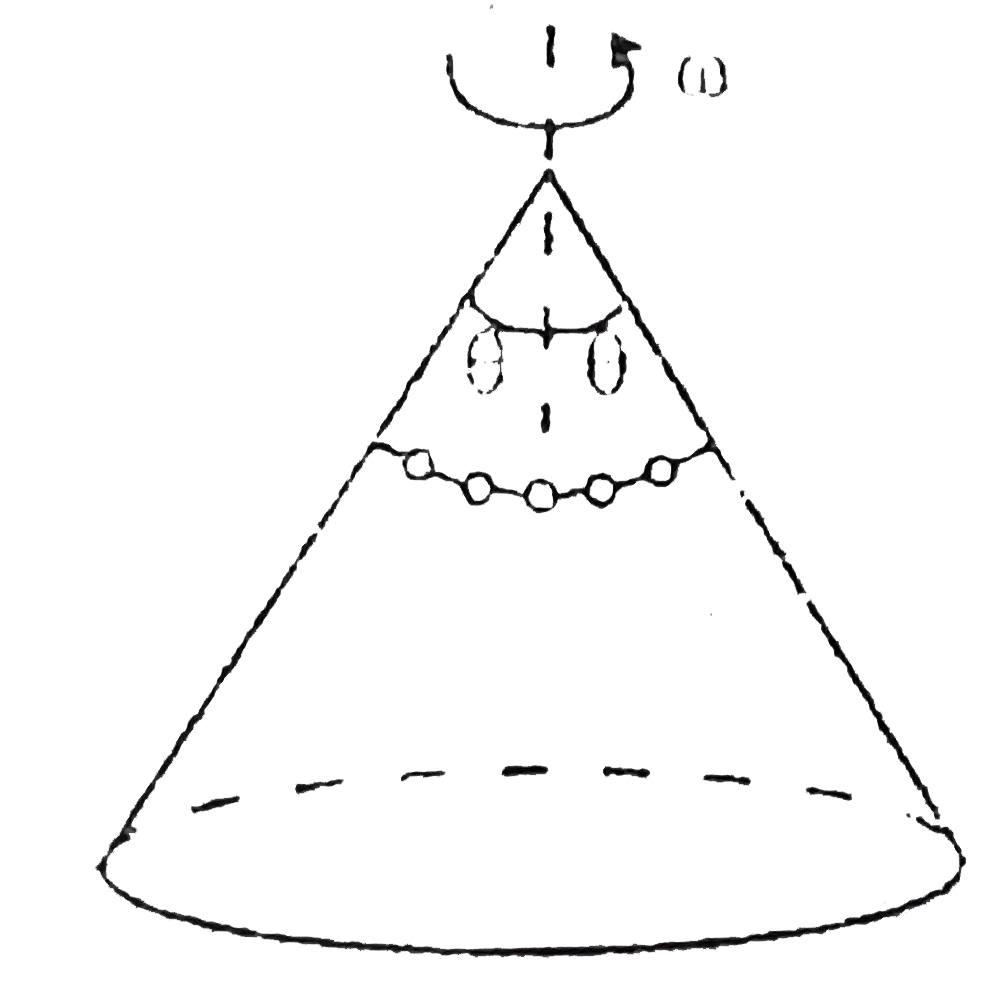
The correct Answer is: $\frac{M}{2 π} (ω^{2} R + g cot θ)$

From F.B.D of chain element
$N sin θ = Δ m g = λ R (2 α) g$ …(i)
$2 T sin α - N cos θ = Δ m ω^{2} R = λ R (2 α) ω^{2} R$ ….(ii)
for small $α, sin α = α$
From (i) and (ii)
$2 T α - \frac{λ R (2 α) g}{sin θ} \times cos θ = λ R (2 α) ω^{2} R$
$\Rightarrow 2 T α = λ R (2 α) ω^{2} R + λ R (2 α) g cot θ$
$\Rightarrow T = λ ω^{2} R^{2} + λ R cot θ$
$= λ R [ω^{2} R + g cot θ]$
$= \frac{M R}{2 π} [ω^{2} R + g cot θ]$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A rope of mass'm' is looped in a circle of radius R and rotated with a constant angular velocity about its axis in gravity free space . Find the tension in the rope ?
A $T = m R ω_{0}^{2}$
B $2 m R π ω^{2}$
C $T = \frac{m R π ω_{0}^{2}}{2 π}$
D $4 m R π ω_{0}^{2}$
Question 2 - Select One
A ring of radius 'r' and mass per unit length 'm' rotates with an angular velocity $' ω'$ in free space then :
ATension in ring is zero
BTension will vary at all points
CTension is constant throughout ring
DTension in string is $m ω^{2} r^{2}$
Question 3 - Select One
A ring of mass m and radius R rests in equilibrium on a smooth cone of semi-vertical angle $45^{\circ}$ as shown. The radius of the cone is 2R. the radius of circular cross section of the ring is $r (r < < R)$ .

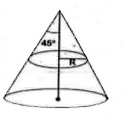
What will be the tension in the ring?
A $\frac{m g}{2 \sqrt{2} π}$
B $\frac{m g}{2 π}$
C $\frac{m g}{\sqrt{2} π}$
D $\frac{\sqrt{2} m g}{π}$

RESONANCE-DAILY PRACTICE PROBLEM-DPP No.32

Home
Ask Doubt
Profile