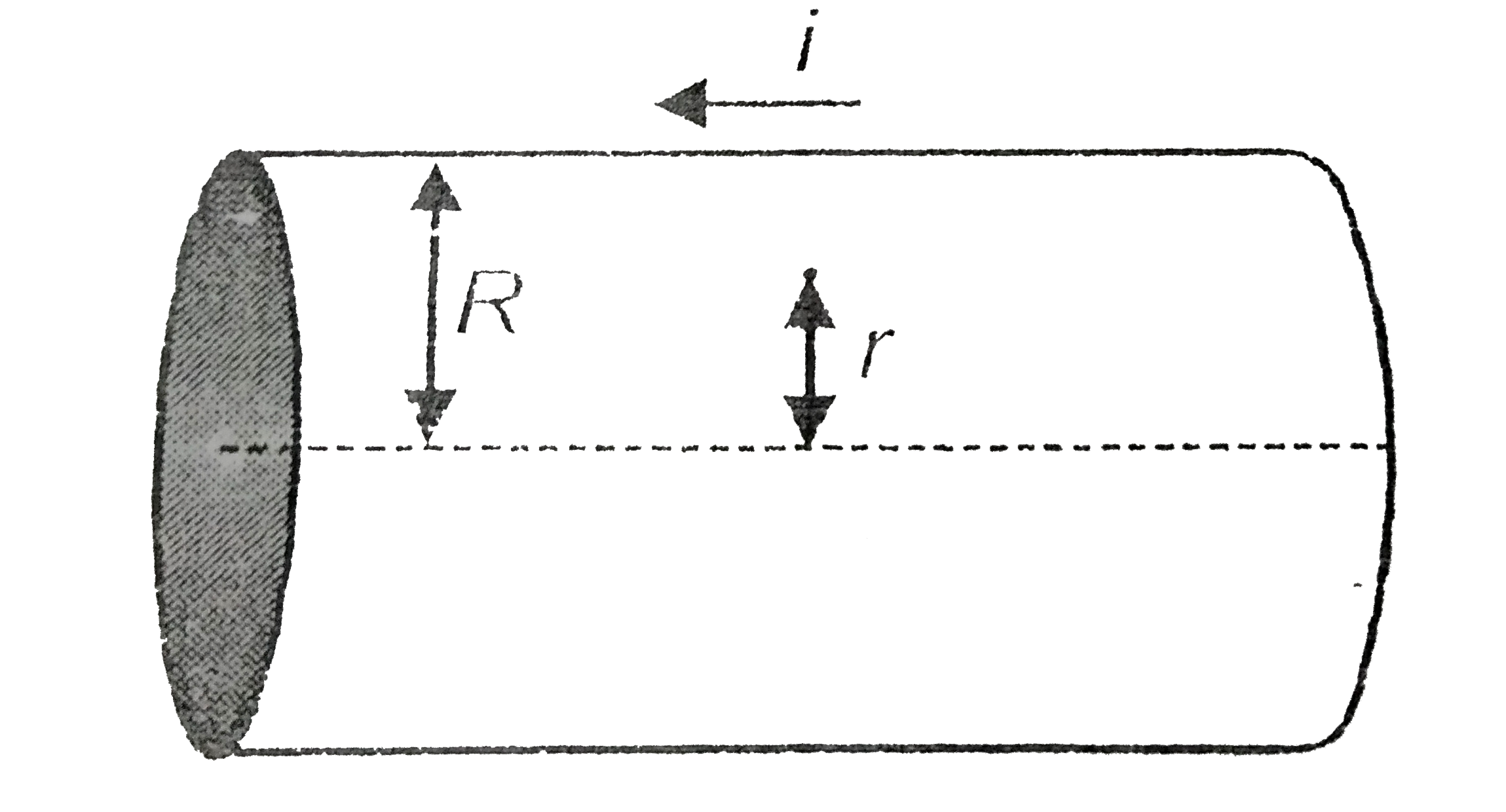
An infinitely long wire of uniform cross section carries a current whose current density varies as j=brα. Where b=107πunit,α=.1unit and r the distance from axis. The magnetic induction at a distance 0.25 from axis is given by n×53x10−2 tesla. Find n
The correct Answer is:5
I=∫(2πx)dx=∫r0bxα2πxdx=2πbra+2a+2
∮B2πr=μ02πbra+2α+2=μ0bra+1α+2⇒n=5
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - LEVEL-VI (SINGLE ANSWER QUESTION)
81 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Level =I (H.W)
42 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT Based Questions
20 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)
9 Videos
Similar Questions
Suppose that the current density in a wife of radius a varies with r according to J=Kr2, where K is a constant and r is the distance from the axis of the wire. Find the megnetic field at a point distance r from the axis when (a) r < a and (b) r > a

View SolutionA long cylinder of uniform cross section and radius R is carrying a current i along its length and current density is uniform cross section and radius r in the cylinder parallel to its length. The axis of the cylinderical cavity is separated by a distance d from the axis of the cylinder. Find the magnetic field at the axis of cylinder.
View Solution
Knowledge Check
An infinitely long cylinderical wire of radius R is carrying a current with current density j=αr3 (where α is constant and r is the distance from the axis of the wire). If the magnetic fixed at r=R2 is B1 and at r=2R is B2 then the ratio B2B1 is
A2B4C6D8A long straight cable contains 7 strands of wire each carrying a current of 5 A. The magnetic induction at a distance of 2 cm from the axis of the cable is
A5×10−5 TB3.5×10−4 TC3.5×10−4 TD1.1×10−3 TThe magnetic field at a distance r from a long wire carrying current i is 0.4 T. The magnetic field at a distance 2r is
A0.2 TB0.8TC0.1 TD1.6 T
Suppose that the current density in a wire of radius a varius with r according to Kr2 where K is a constant and r is the distance from the axis of the wire. Find the magnetic field at a point at distance r form the axis when (a) rlta and (b) rgta.
View SolutionIn a long cylindrical wire of radius R, magnetic induction varies with the distance from axis as B=crα. Find the function of current density in wire with the distance from axis of wire.
View SolutionA long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J=kr2, where, k is a constant. Find an expression for the magnetic field B at a distance r(<R) from the axis
View SolutionMagnetic field at a distance r from an infinitely long straight conductor carrying steady varies as
View SolutionWhich of the following graphs shows the variation of magnetic induction B with distance r from a long wire carrying current
View Solution
