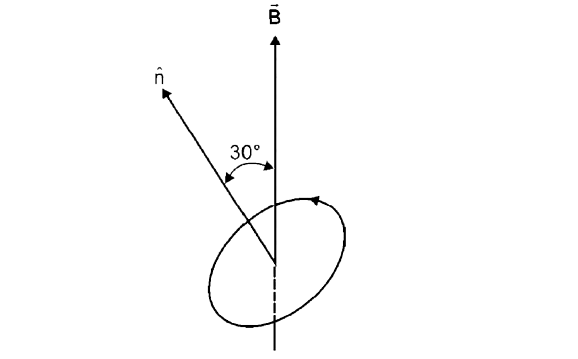
An electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius R.
(i) Obtain an experssion for the orbital magnetic dipole moment of the electron.
(ii) The atom is placed in a uniform magnetic induction →B such that the plane - normal of the electron - orbit makes an angle of 30∘ with the magnetic induction . Find the torque experienced by the orbiting electron.
(i) Orbital magnetic dipole moment M=eT×πR2
⇒M=12eωR2
According to orhr's postualtes
mRω2=nh2π⇒M=nhe4πm
(ii)τ=MBsinθ=nhe4πm×Bsin30∘=nheB8πm
filed due to other semicircle KNM.
Therefore,
→B=−μ0I4R(−ˆi)+μ0I4R
⇒→B=−μ04Rˆi+μ0I4R(−ˆi+ˆj)
∣∣→B due to a circular current carrying loop is μ0I2R For semicircle it is half ∣
Therefore magnetic force acting on the particle
→Fq{(−v0ˆi)×(−ˆi+ˆj)×μ0I4R}=−μ0qv0I4Rˆk
(B)→FKLM=→FKNM=→FKM
and Total force on the loop =4BIRˆi
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - LEVEL-VI (SINGLE ANSWER QUESTION)
81 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Level =I (H.W)
42 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT Based Questions
20 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)
9 Videos
Similar Questions
An electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in the circular orbit of radius R as shown in figure.

Obtain an expression for the orbital magnetic dipole moment of the electron.
View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in a circular orbit of radius R.

(i) The expression for the orbital magnetic moment of the electrton is ehnπm. Find n □
(ii) The atom is placed in a uniform magnetic induction B such that the normal to the plane of electron’s orbit makes an angle of 30∘ with the magnetic induction. The torque experienced by the orbiting electron is ehBnπm. Find n □
View Solution
Knowledge Check
An electron in the ground state of hydrogen atom is revolving in anticlockwise direction in circular orbit of radius R. The orbital magnetic dipole moment of the electron will be
Aeh4πmBeh2πmCeh24πmDe2h4πmMagnetic dipole moment of revolving electron is
AeL2mBe2mCe2MLDemL
An electron in the ground state of hydrogen atom is revolving in anticlockwise direction in circular orbit of radius R. The orbital magnetic dipole moment of the electron will be
View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in the circular orbit of radius R as shown in figure.
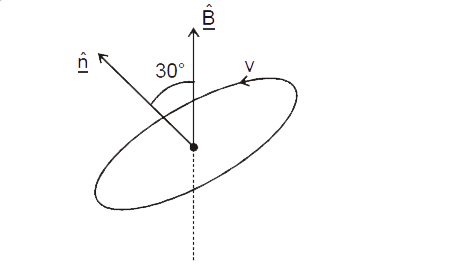
The atom is placed in a uniform magnetic induction B such that the plane normal of the electron orbit makes an angle 30∘ with the magnetic induction. Find the torque experienced by the orbiting electron.
View SolutionThe minimum magnetic dipole moment of electron in hydrogen atom is
View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clock wise direction in a circular orbit. The atom is placed in a magnetic filed such that the normal to the electron orbit makes an angle of 30° with the magnetic field. Find the torque experienced by the orbiting electron.
View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in the circular orbit of radius R as shown in figure.

The atom is placed in a uniform magnetic induction B such that the plane normal of the electron orbit makes an angle 30∘ with the magnetic induction. Find the torque experienced by the orbiting electron.
View SolutionShow that the orbital magnetic dipole moment of a revolving electron isevr/2.
View Solution
