A wire carrying a current I is bent into the shape of an exponential spiral, r=eθ, from θ=0 to θ=2π as shown in figure (a0 . To complete a loop, the ends of the spiral are connected by a straight wire along the x− axis. Find the magnitude and direction of →B at the origin.

μ0I4π(1−e−2π)
μ0I3π(1−e−2π)
μ0Iπ(1−e−2π)
μ0I2π(1−e−2π)
The correct Answer is:A
Before we start with the problem , we must know and keep in mind that the angle β between a radial line and its tangent line at any point on the curve r=f(θ) related to the function as
tanβ=rdrdθ

Thus in this case, we have r=eθ and so we get tanβ=1 and β=π4. Therefore, the angle between d→1 and ˆr is (π−β)=3π4 . Alsod→1=drsin(π4)=√2dr
From Biot − Savart's law, we know that there is no contribution from the straight portion of the wire since d→1×→r=0.For the field of the spiral, we have
dB=μ0I4π(d→1׈r)r2⇒B=μ0I4π∫2πθ=0∣∣d→1∣∣sinθ|→r|r2
=μ0I4π∫2πθ=0√2dr[sin(3π4)]1r2
⇒B=μ0I4π∫2πθ=0r−2dr=−μ0I4π(r−1)∣∣∣2πθ=0
Substitute r=eθ, we get
⇒B=−μ0I4π(e−θ)∣2π0=−μ0I4π(e−2π−eθ)
=μ0I4π(1−e−2π) out of the page.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Level =I (H.W)
42 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Level -II (H.W)
37 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - LEVEL-V (SINGLE ANSWER QUESTION)
85 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)
9 Videos
Similar Questions
The segment of wire shown in figure carries a current of i=5.0A where the radius of the circular arc is R=3.0cm. Determine the magnitude and direction of the magnetic field at the origin.
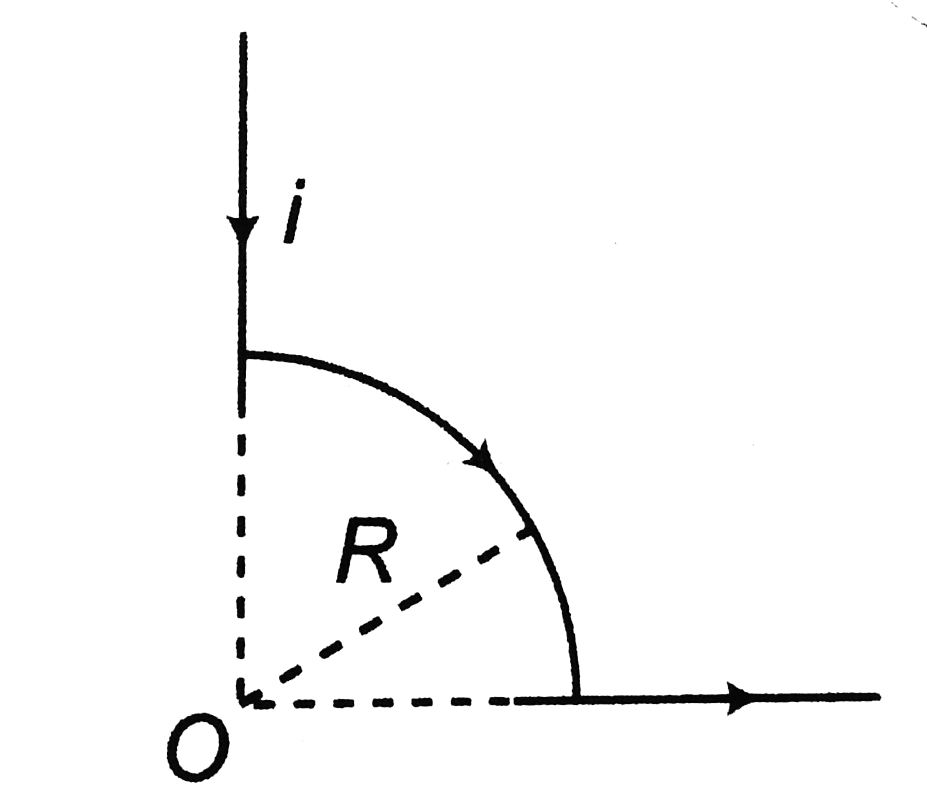
View SolutionThe segment of wire shown in figure carries a current of i=5.0A where the radius of the circular arc is R=3.0cm. Determine the magnitude and direction of the magnetic field at the origin.

View Solution
Knowledge Check
The straight wire AB carries a current I. The ends of the wire subtend angles θ1 and θ2 at the point P as shown in figure. The magnetic field at the point P is
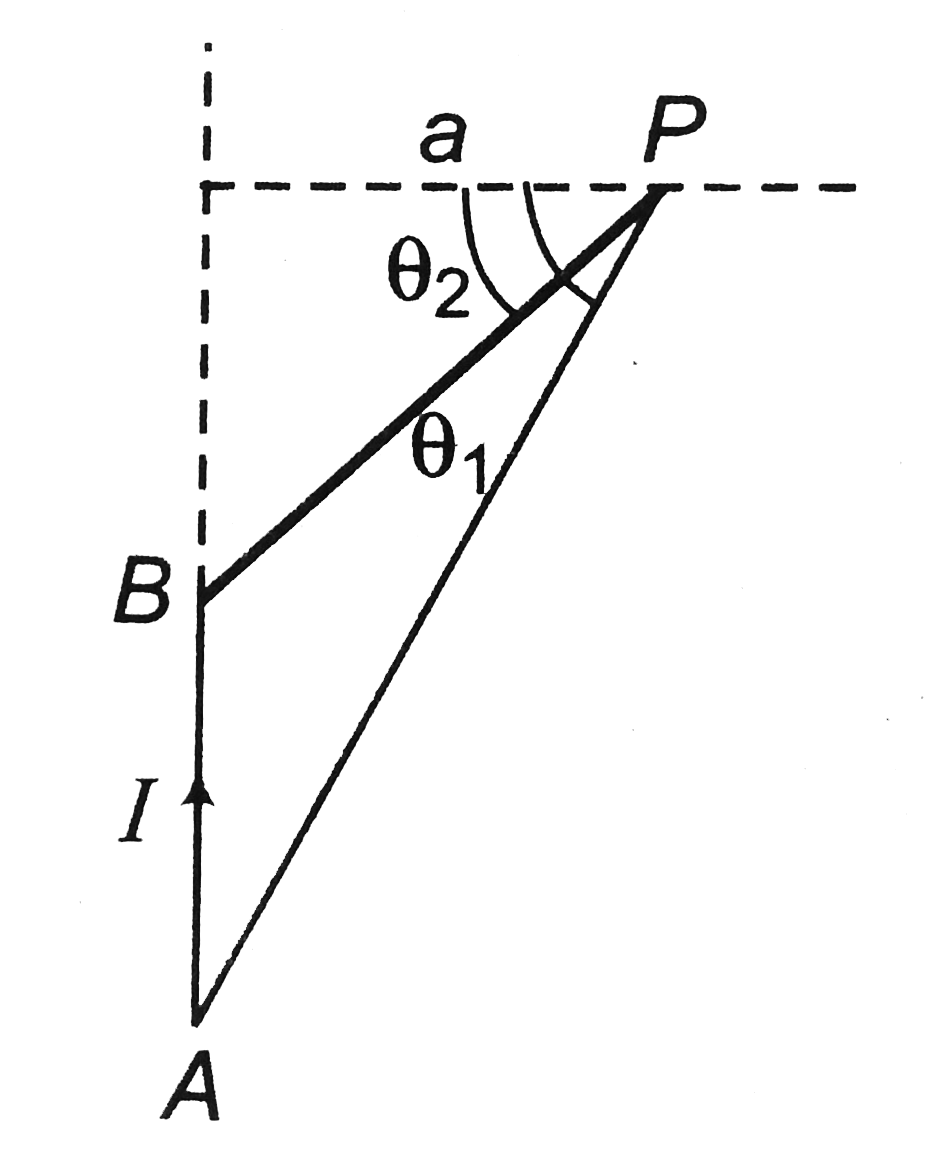 Aμ0I4πa(sinθ1−sinθ2)Bμ0I4πa(sinθ1+sinθ2)Cμ0I4πa(cosθ1−cosθ2)Dμ0I4πa(cosθ1−cosθ2)
Aμ0I4πa(sinθ1−sinθ2)Bμ0I4πa(sinθ1+sinθ2)Cμ0I4πa(cosθ1−cosθ2)Dμ0I4πa(cosθ1−cosθ2)
The straight wire AB carries a current I. The ends of the wire subtend angles θ1 and θ2 at the point P as shown in figure. The magnetic field at the point P is

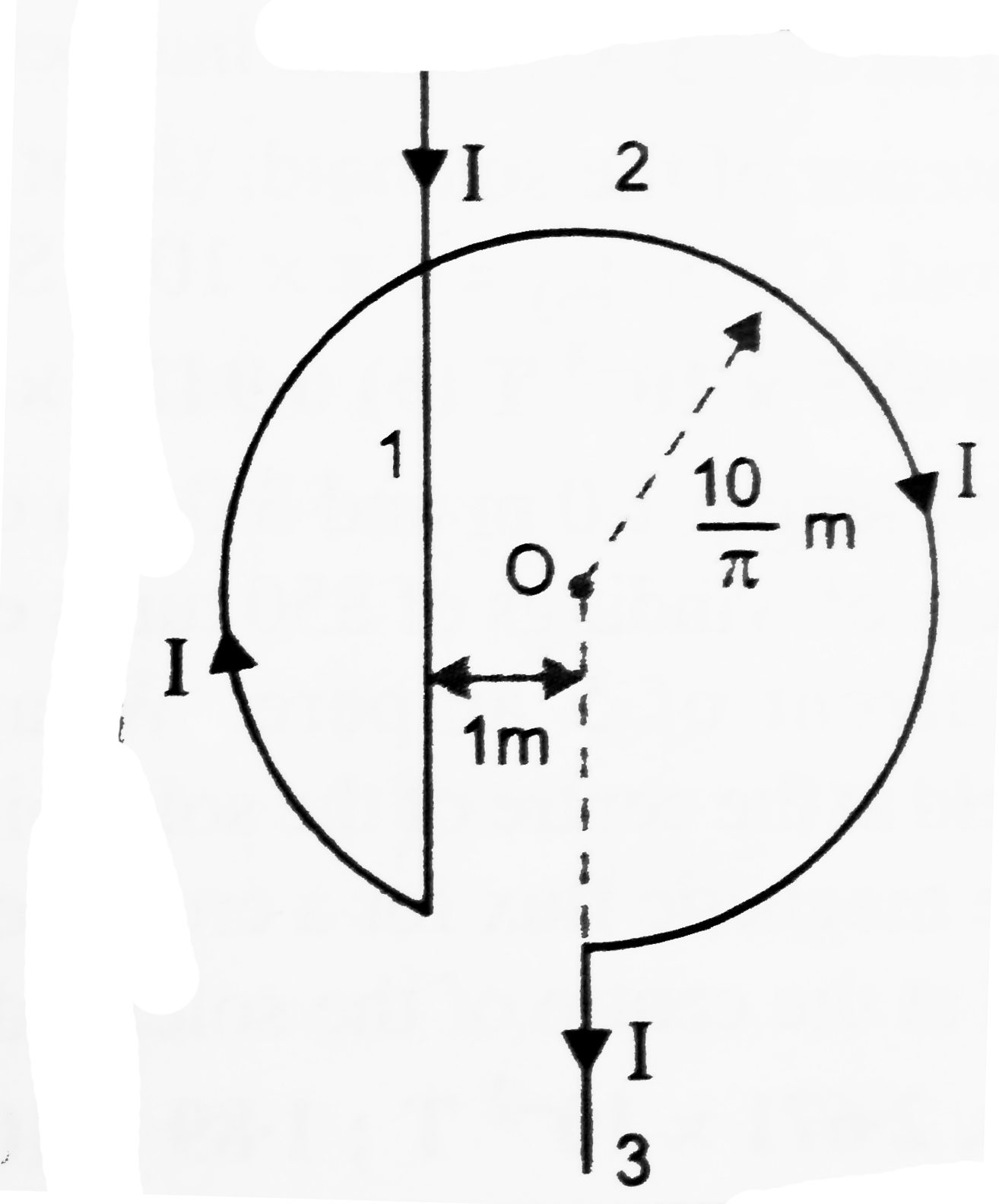
View SolutionA long straight wire carrying current I is bent into the shape as shown in the figure. The circular portion of the wire has radius (10/π)m. The centre of this circle is at a distance 1m from the straight portion of the wire. What is the magnitude of the magnetic field at the centre of the circular portion? Given π2=10.
View SolutionA straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the fig. Find the magnitude and direction of the magnetic field at the centre of the arc.

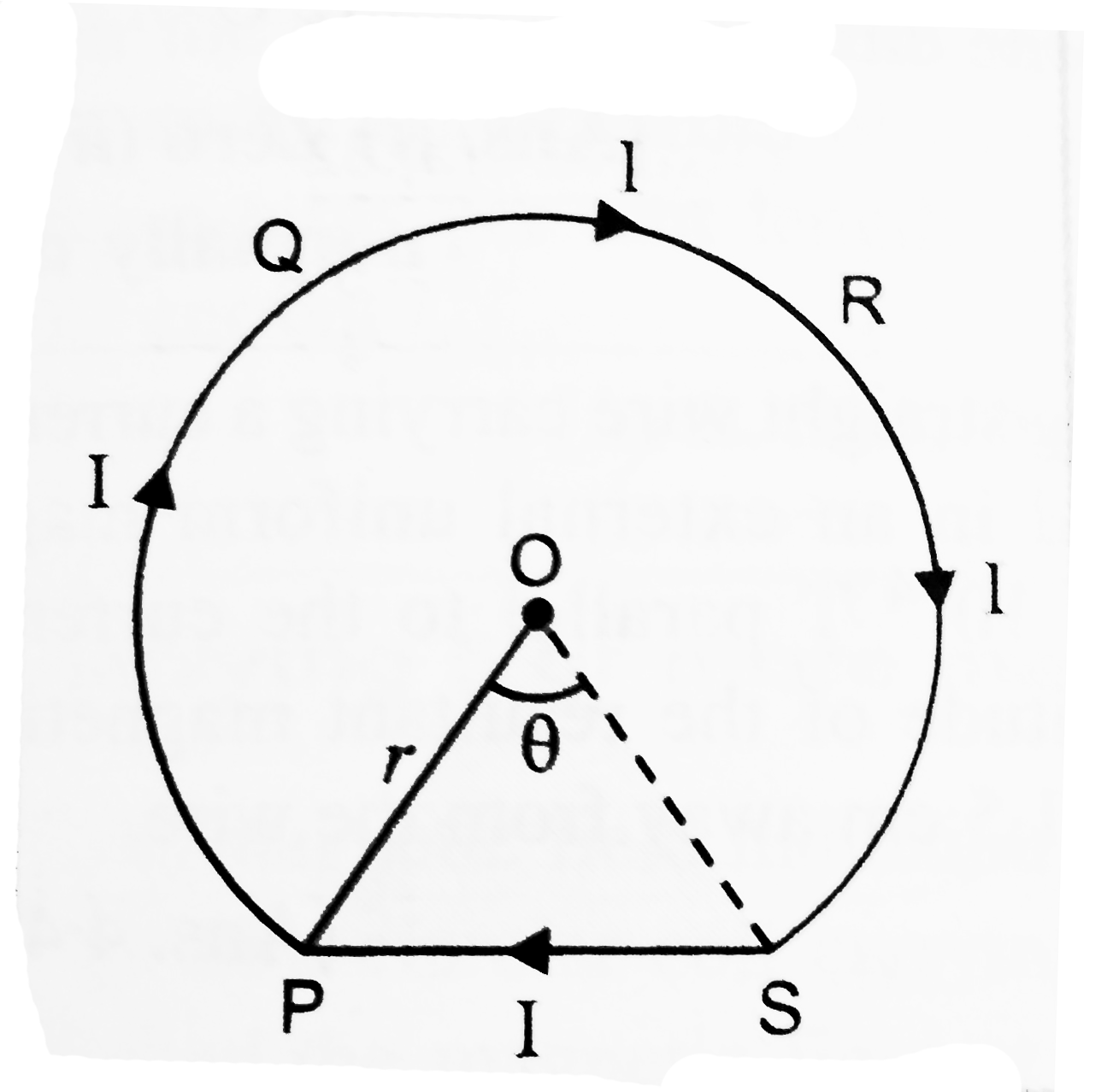
View SolutionA current I(=4A) flows along a thin wire PQRS shaped as shown in figure. The radius of the curved part of the wire is 10⋅0cm. The angle θ=90∘. Find the magnitude of the total magnetic field at the point O.
View Solution(a) Find the magnetic field at the point O if the wire carrying a current i has the shape shown. The radius of the current part of the wire is R, the linear parts of the wire are very long.
(i)
(ii)
(iii)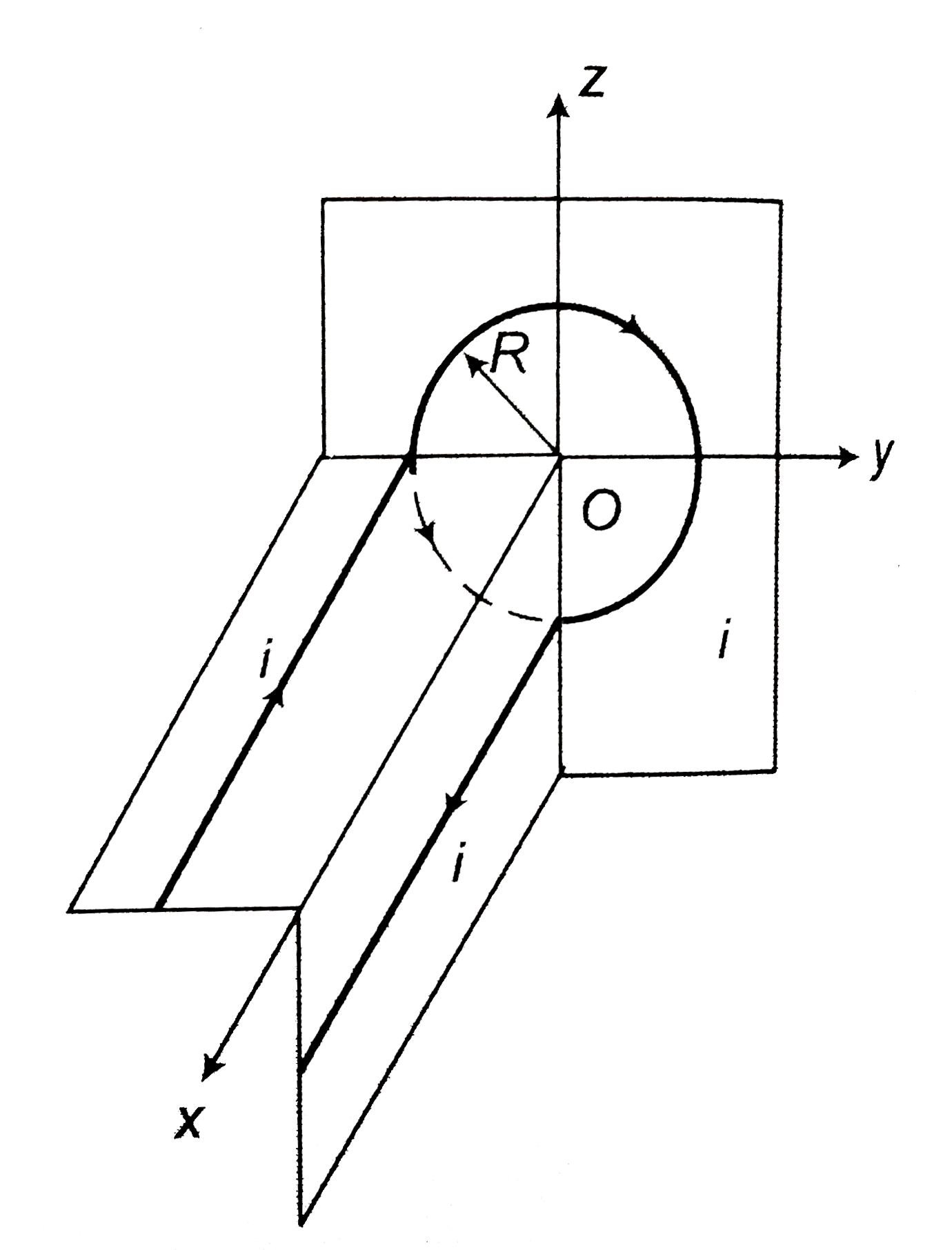
(b) A long straight wire along the z-axis carriers a current i in negative z-direction. Find magnetic field in vector from at a point having co-ordinates (x,y) on z=0 plane.
(c) A non-coplaner loop of conducting wire carrying a current I is placed as shown in the figure. Each of the straight sections of the loop of length 2a. find unit vector along magnetic field magnetic filed at the point P(a,0,a).
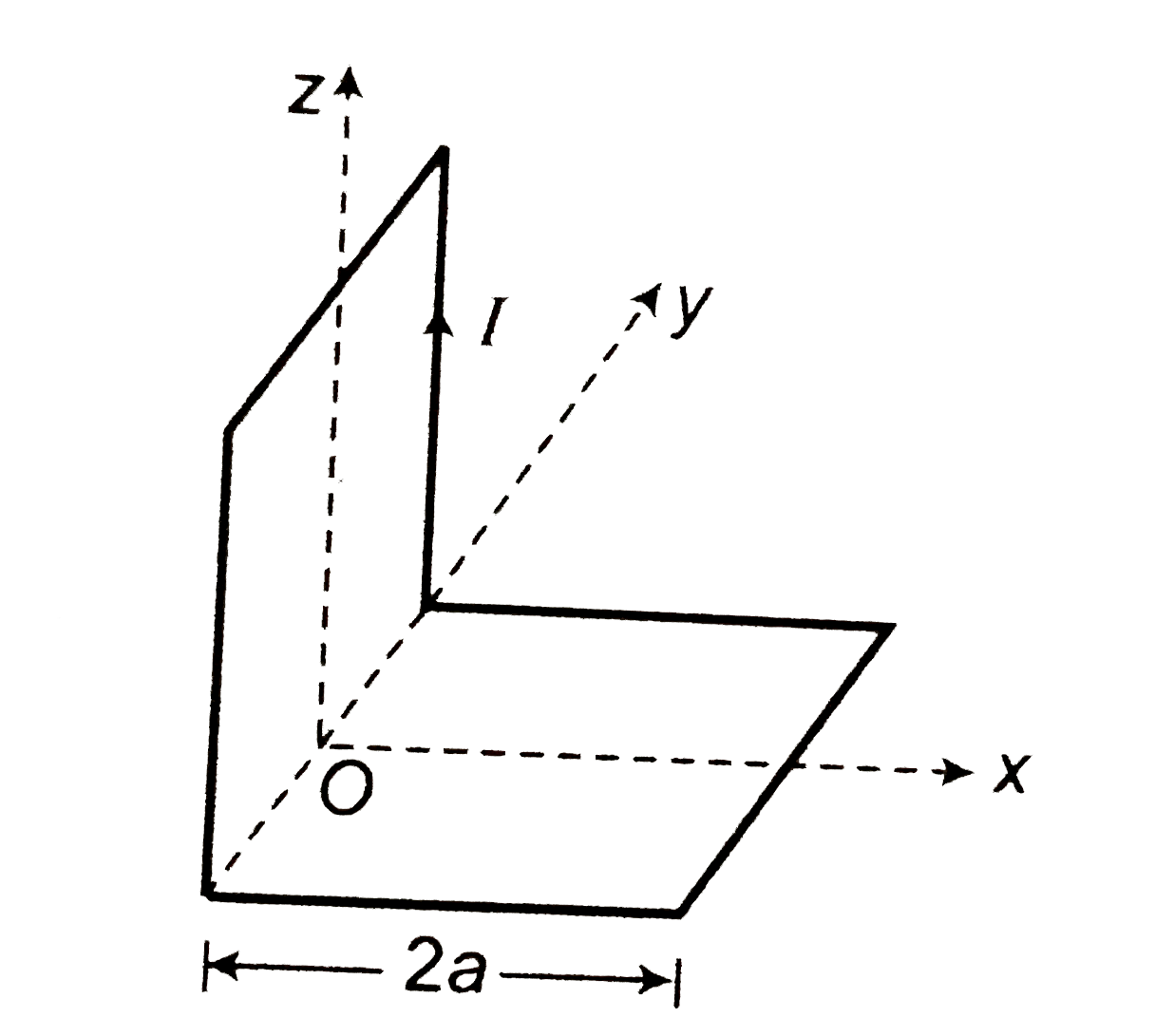
View SolutionA pair of stationary and infintely long bent wires are placed in the XY planes as shown in fig. The wires carry currents of I=10amperes each as shown . The segments PandQ are parallel to the Y−aξs such that OS=OR=0.02m. Find the magnitude and direction of the magnetic induction at the origin O.
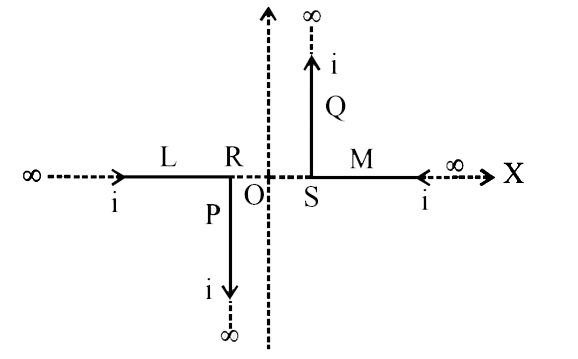
View SolutionA pair of stationary and infintely long bent wires are placed in the XY planes as shown in fig. The wires carry currents of I=10amperes each as shown . The segments PandQ are parallel to the Y−aξs such that OS=OR=0.02m. Find the magnitude and direction of the magnetic induction at the origin O.

View Solution
