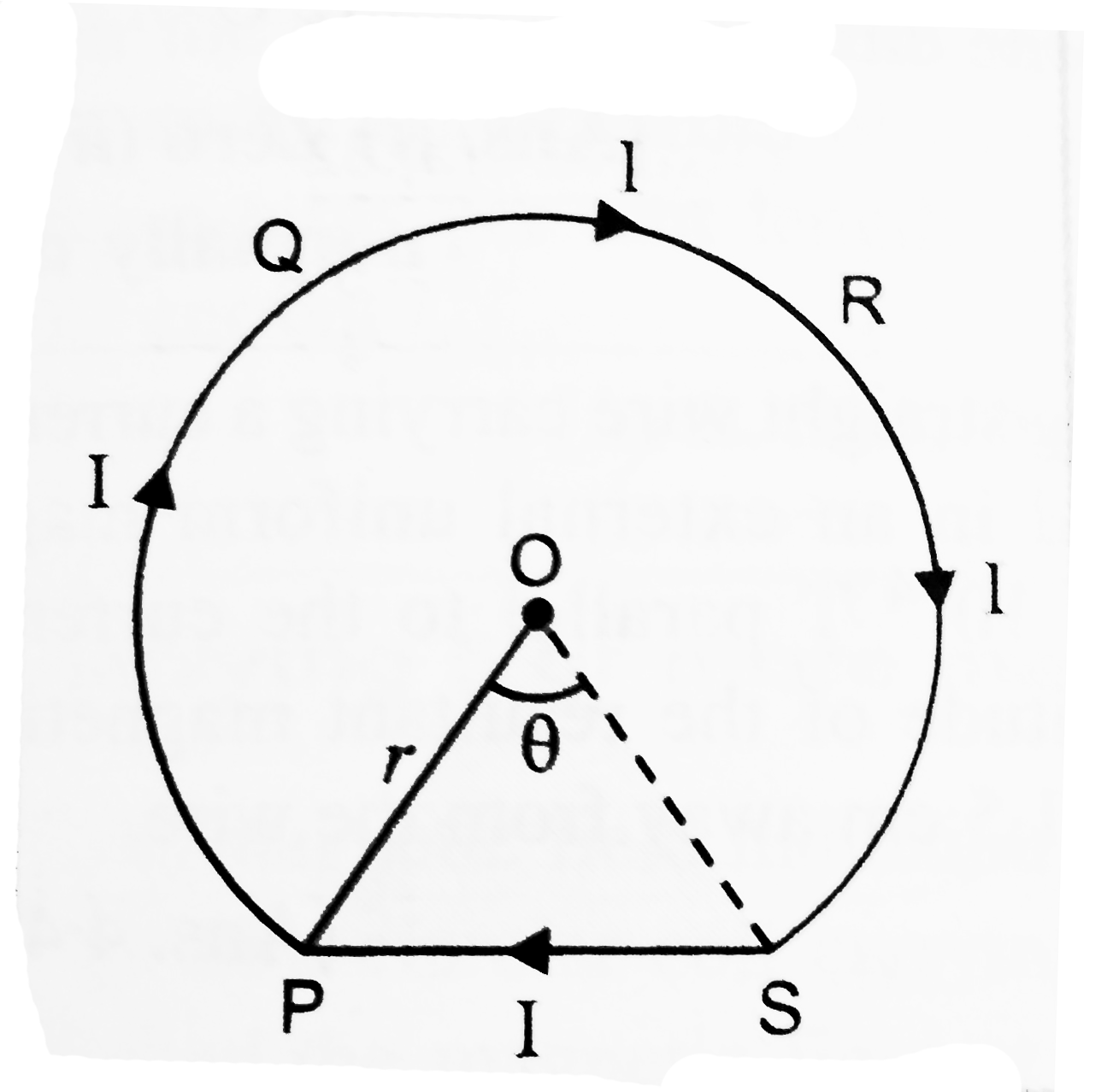
A current I(=4A) flows along a thin wire PQRS shaped as shown in figure. The radius of the curved part of the wire is 10⋅0cm. The angle θ=90∘. Find the magnitude of the total magnetic field at the point O.
The correct Answer is:2⋅68×10−5T
Here, I=4A, r=10⋅0cm=0⋅10cm,
As ∠POS=90∘ and PO=OS=r,
so ∠OPS=∠OSP=45∘
Angle subteded at O by curved wire PQRS
=3π2rad
Magnetic field at O due to current through portion SP of wire is
B1=μ04πIrcosθ/2[sinθ2+sinθ2]
=μ04πIr×2tanθ2
It is acting normally downwards.
Magnetic field at O due to current through portion PQRS of wire is
B2=μ04πIr[2π−π/2]=μ04πIr×3π2
It is acting normally downwards.
Total magnetic field at point O is
B=B1+B2=μ04πIr[2tanθ2+3π2]
=10−7×40⋅1[2tan90∘2+3π2]
=10−7×40[2tan45∘+3π2]
=10−7×40[2×1+32π]
=2⋅68×10−5T acting normally downwards.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (a)1videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (c)1videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Value Based Questions2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS2videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Multiple choice questions1videos
OPTICS
Similar Questions
Find the magnetic induction of the field at the point O at a loop with current I, whose shape is illustrated in figure
(a)In figure a the radii a and b, as well as the angle φ are known
(b)In figure b,the raidus a and the side b are known.
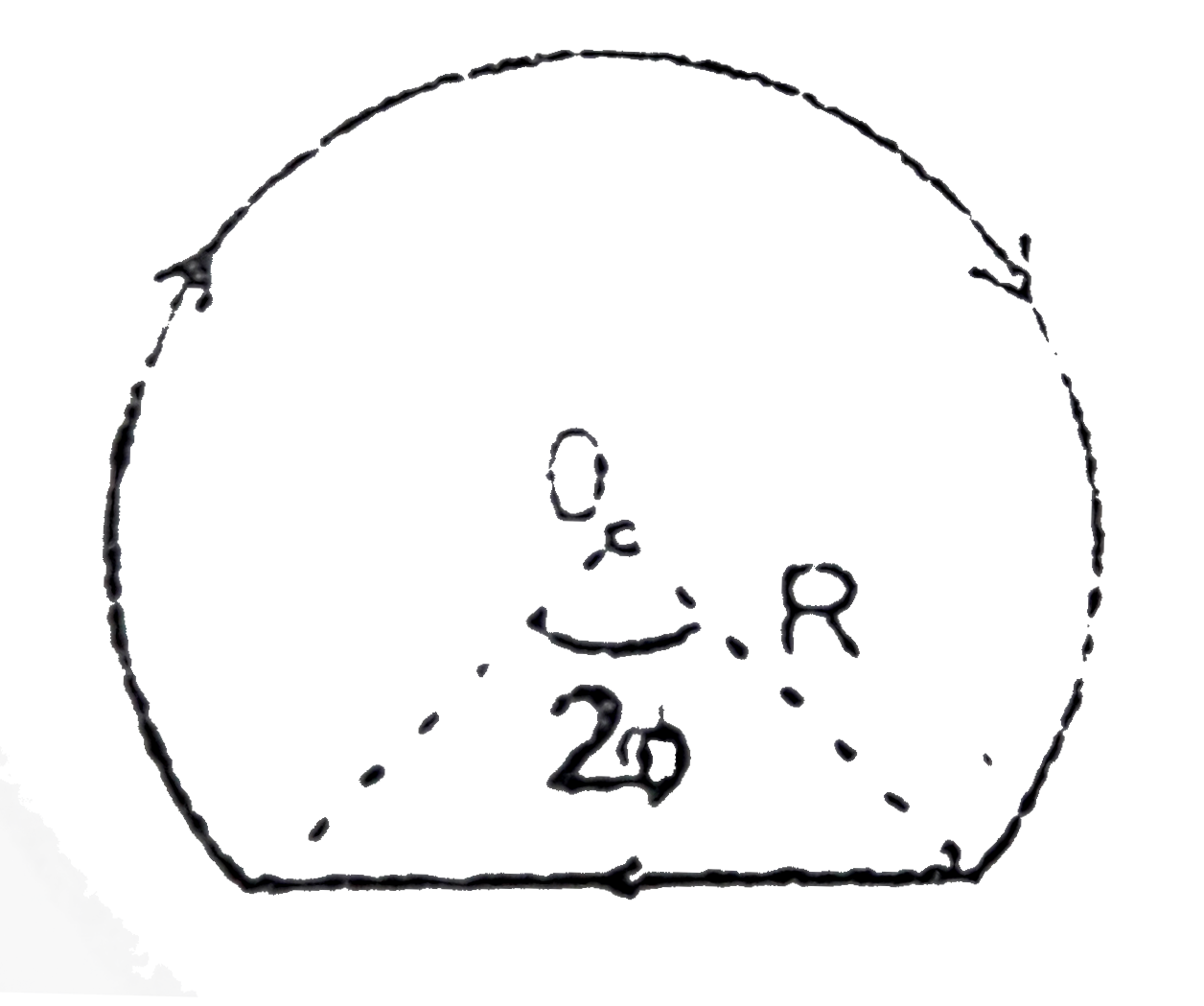
(c)A current I=5.0A flows along a thin wire shaped as shown in figure.The radius of a curved part of the wire is equal to R=120mm,the angle 2φ=90∘.Find the magnetic induction of the field at the point O.
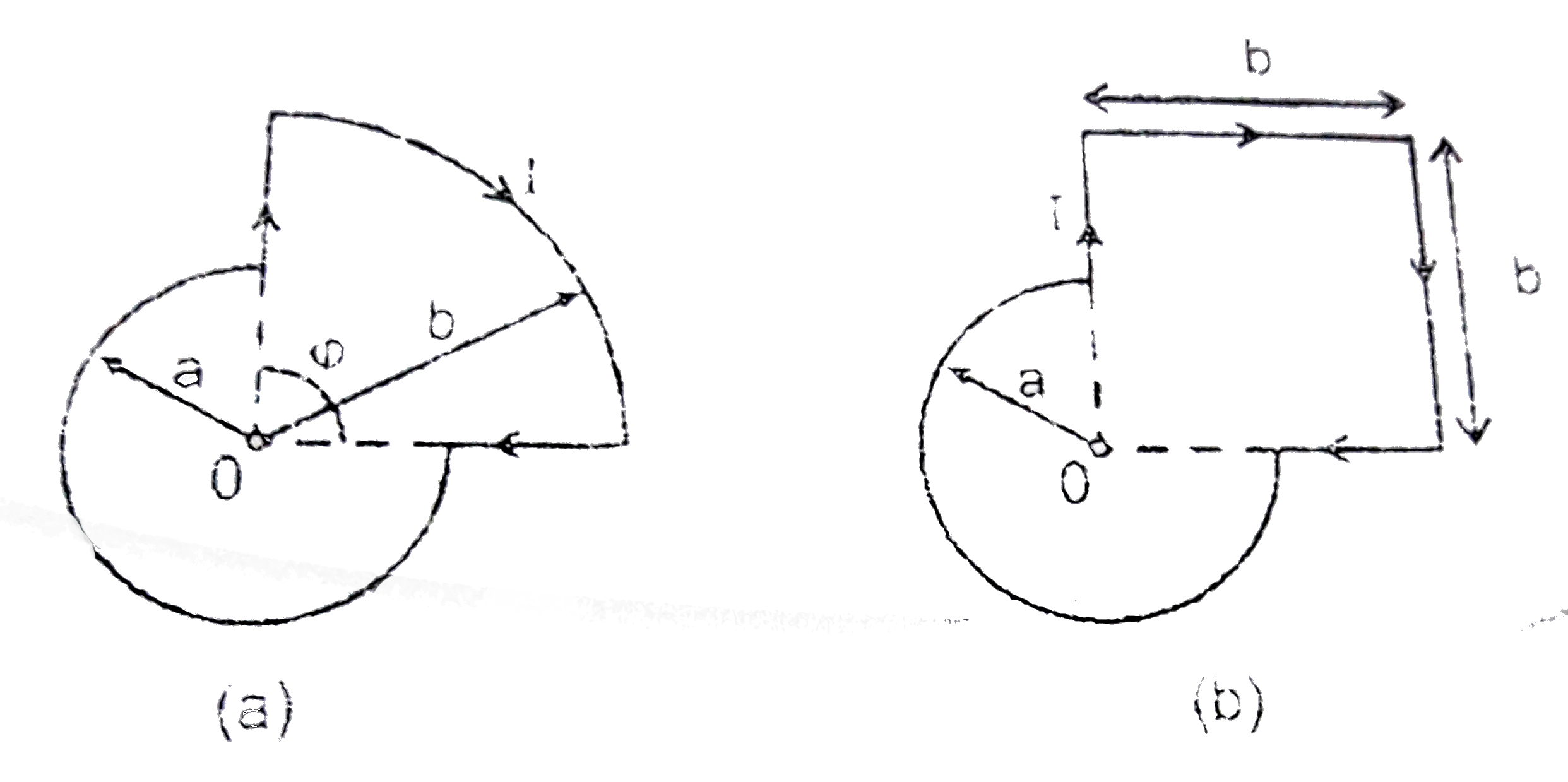
 View Solution
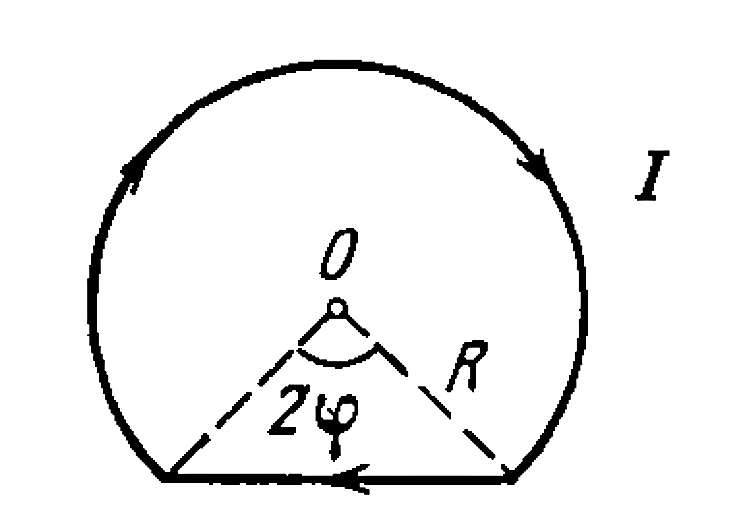
View SolutionA current I=5.0A A flows along a thin wire shaped as shwon in Fig. The radius of a curved part of the wire is equal to R=120mm, the angle 2φ=90∘. Find the magentic induction of the field at the point O.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A current I flows along a thin wire shaped as shown in figure. The radius of the curved part of the wire is r. The field at the centre O of the coil is:
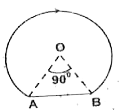 Aμ04.irBμ02πrCμ0I2πrDμ0I8πr(3π+4)
Aμ04.irBμ02πrCμ0I2πrDμ0I8πr(3π+4) - Question 2 - Select One
Current I is flowing in a conductor shaped as shown in the figure. The radius of the curved part is r and the length of straight portion is very large. The value of the magnetic field at the centre will be
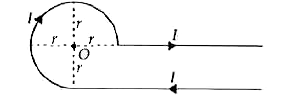 Aμ04πr(π2+1)Bμ04πr(π2−1)Cμ04πr(3π2+1)Dμ04πr(3π2−1)
Aμ04πr(π2+1)Bμ04πr(π2−1)Cμ04πr(3π2+1)Dμ04πr(3π2−1) - Question 3 - Select One
The straight wire AB carries a current I. The ends of the wire subtend angles θ1 and θ2 at the point P as shown in figure. The magnetic field at the point P is
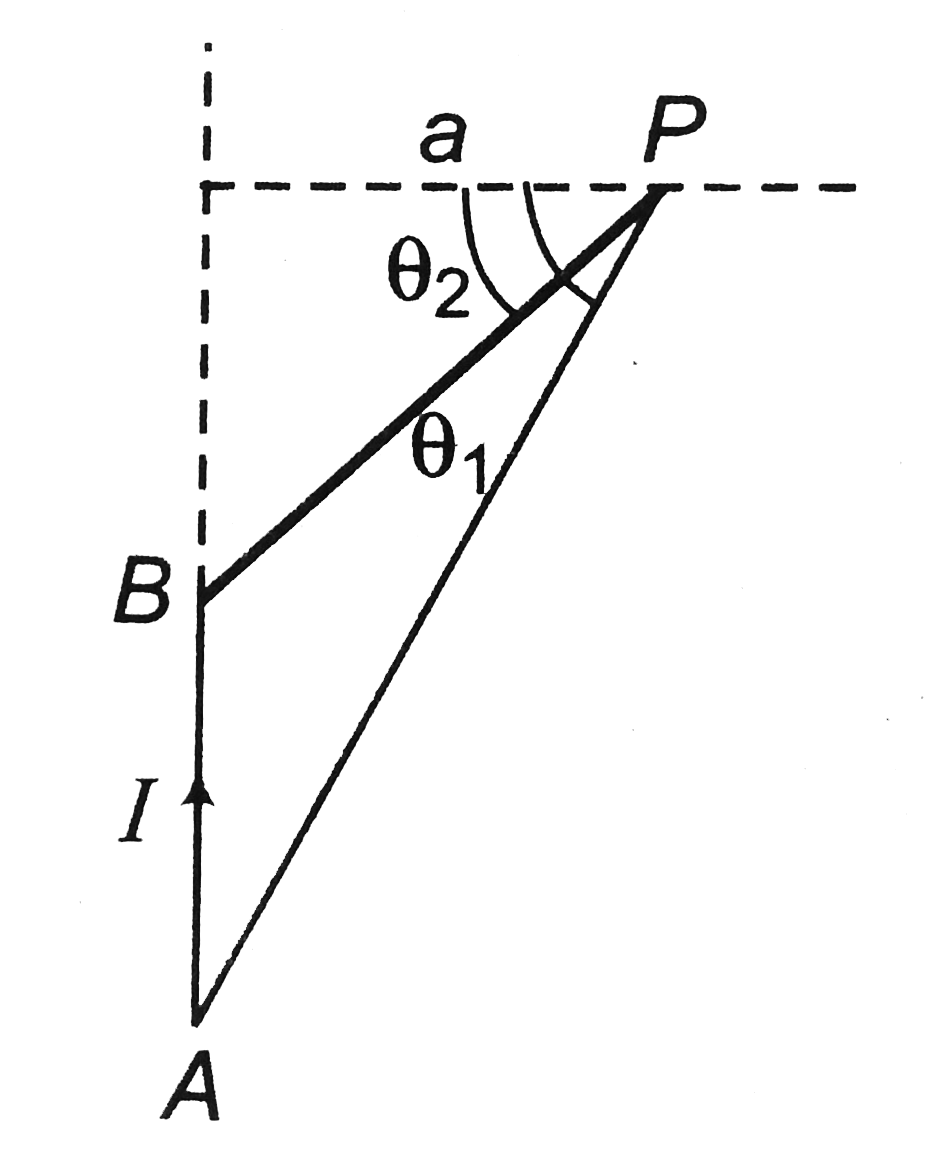 Aμ0I4πa(sinθ1−sinθ2)Bμ0I4πa(sinθ1+sinθ2)Cμ0I4πa(cosθ1−cosθ2)Dμ0I4πa(cosθ1−cosθ2)
Aμ0I4πa(sinθ1−sinθ2)Bμ0I4πa(sinθ1+sinθ2)Cμ0I4πa(cosθ1−cosθ2)Dμ0I4πa(cosθ1−cosθ2)
A current I is flowing in a conductor shaped as shown in figure. The radius of the curved part is r and length of straight portion is very large. Find the magnetic field induction at the centre O.
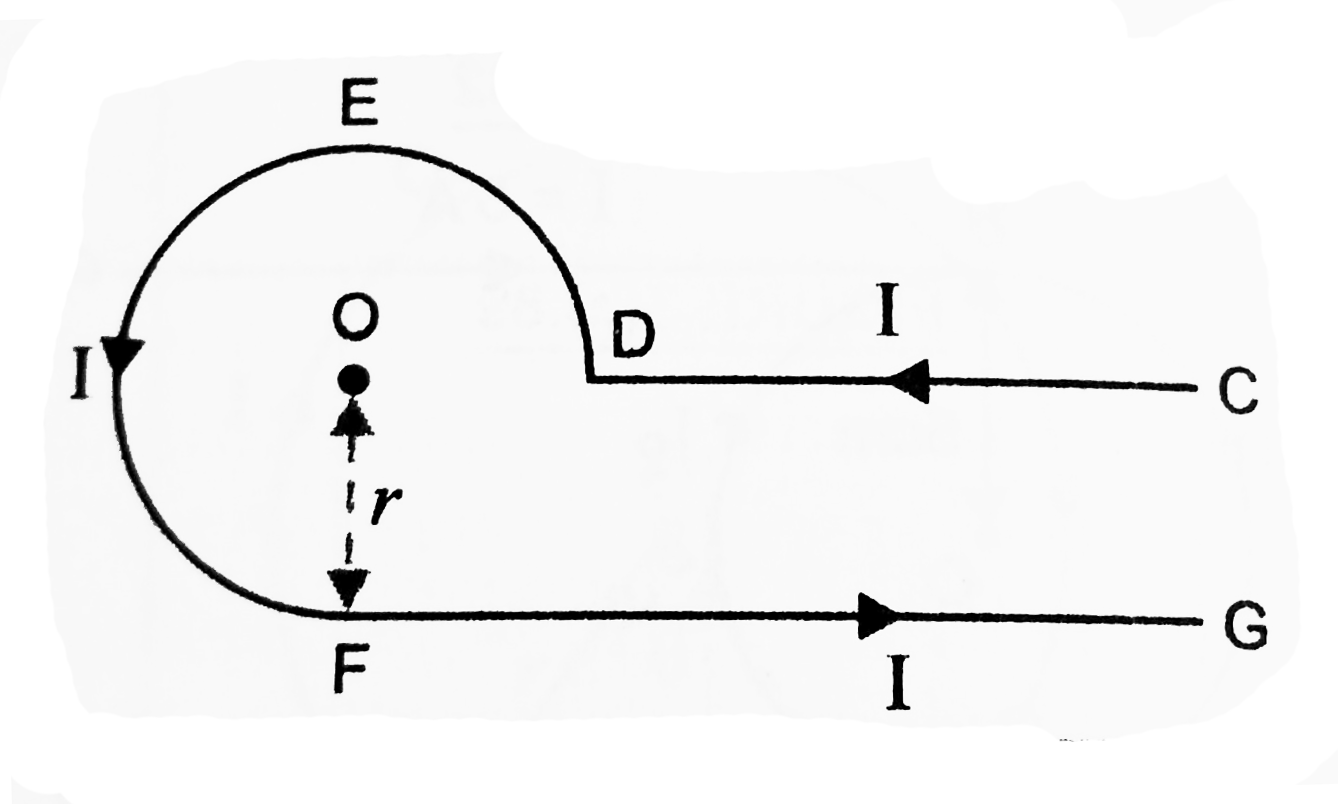 View Solution
View SolutionA current i is flowing in a conductor PQRST shaped as shown in the figure. The radius of curved part QRS is r and length of straight portions PQ and ST is very large. The magnetic field at the centre O of the curved part is -
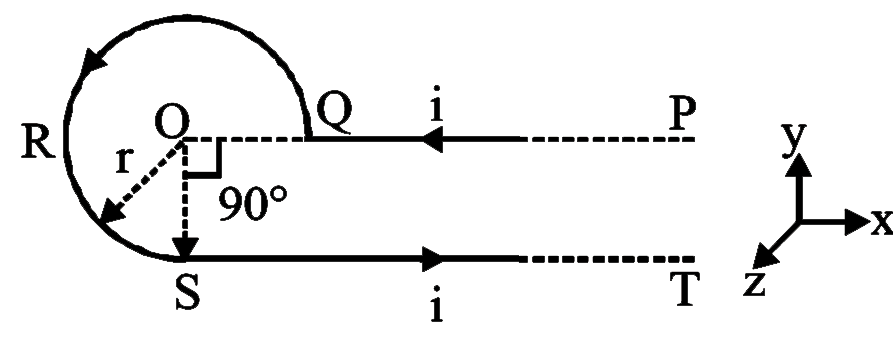 View Solution
View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be
 View Solution
View SolutionA long straight wire carrying current I is bent into the shape as shown in the figure. The circular portion of the wire has radius (10/π)m. The centre of this circle is at a distance 1m from the straight portion of the wire. What is the magnitude of the magnetic field at the centre of the circular portion? Given π2=10.
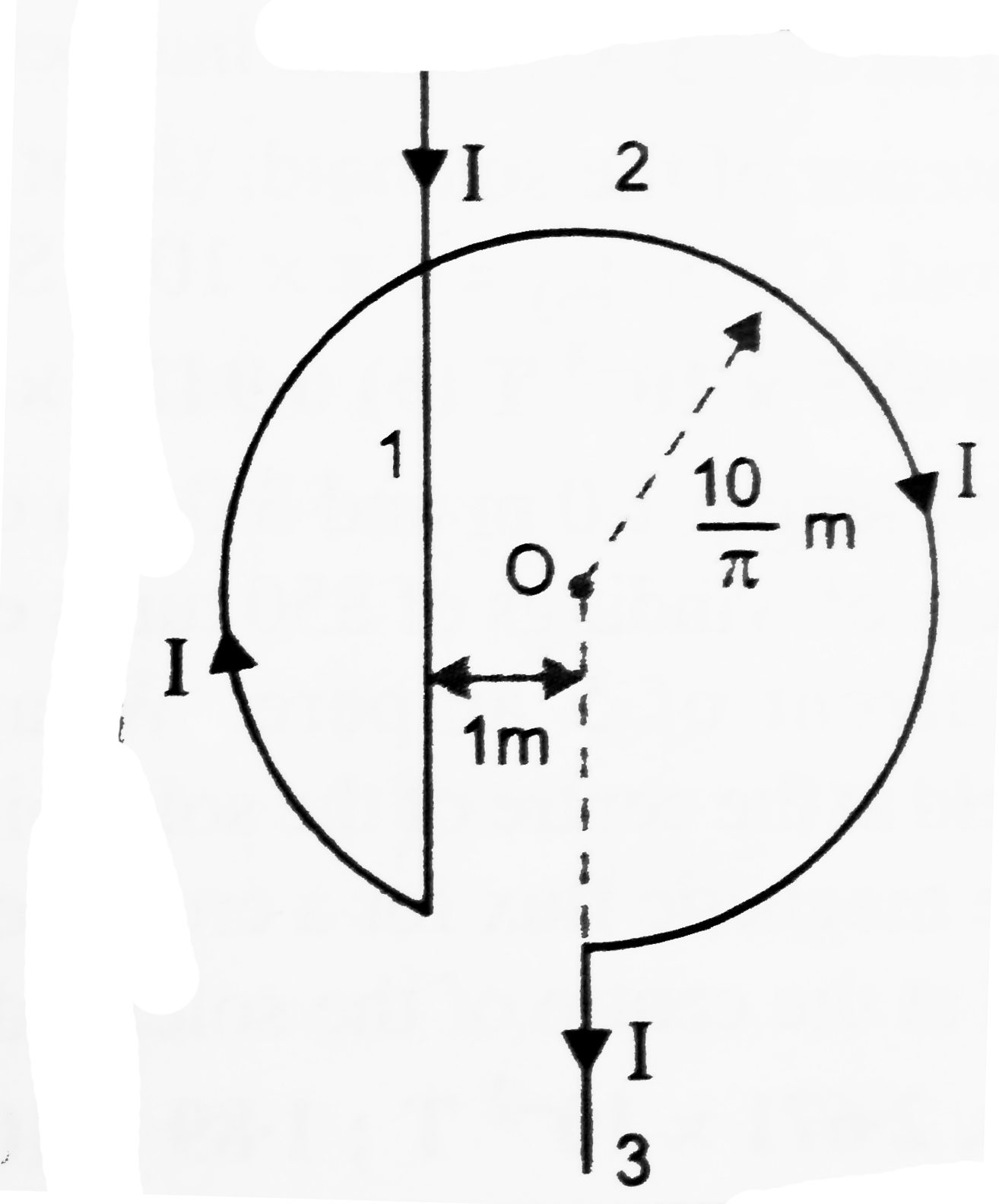 View Solution
View SolutionIn the figure, the curved part represents arc of a circle of radius x. If it carries a current I then the magnetic field at the point O is
 View Solution
View Solution

