There is region of space where uniform magnetic field of induction B exists. The field exists at all points for which x− coordingates are positive. The direction of field ia along negative z axis.
Now a certain charged particle of mass m and charge q a certain speed enters in this region. A magnetic field at a point whose coordinates are x=0,y=−d and z=0 . Magnetic force will start acting on the particle and particle moves in a uniform circular motion, such that origin becomes centre of circular path described by it
The speed of the charge particle will be
qBm
qdm
qbd2m
qBdm
The correct Answer is:D
Radius of circular path will be equal to d=mvqB⇒v=qBdm
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level =I (H.W)
Explore 42 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level -II (H.W)
Explore 37 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:LEVEL-V (SINGLE ANSWER QUESTION)
Explore 85 Videos
- MAGNETISM AND MATTERBook:NARAYNAChapter:MAGNETISM AND MATTERExercise:EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
Explore 17 Videos
- NUCLEAR PHYSICSBook:NARAYNAChapter:NUCLEAR PHYSICSExercise:LEVEL-II-(H.W)
Explore 9 Videos
Similar Questions
A charged particle enters a region of uniform magnetic field at an angle of 85∘ to the magnetic line of force . The path of the particle is a circle .
View SolutionThe figure shows two regions of uniform magnetic field of strengths 2B and 2B. A charged particle of mass m and charge q enters the region of the magnetic field with a velocity υ=qBwm, where w is the width of each region of the magnetic field. The time taken by the particle to come out of the region of the magnetic field is
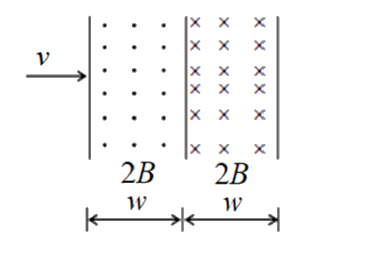
View Solution
Knowledge Check
There is region of space where uniform magnetic field of induction B exists. The field exists at all points for which x− coordingates are positive. The direction of field ia along negative z axis.
Now a certain charged particle of mass m and charge q a certain speed enters in this region. A magnetic field at a point whose coordinates are x=0,y=−d and z=0 . Magnetic force will start acting on the particle and particle moves in a uniform circular motion, such that origin becomes centre of circular path described by it
The particle enters into the region of magnetic field along a directionAparallel to y− axisBat an angle 37∘ with x− axisCalong x− axisDalong a direction of 45∘ with x− axisA charged particle enters a uniform magnetic field perpendicular to it. The magnetic field
Aincreases the K.E. of the particleBdecreases the K.E. of the particleCchanges the direction of motion of the particleDdoes both (a) and ( c)A long straight wire along the z−aξs carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
Aμ0I(yˆi)−xˆj2π(x2+y2)Bμ0I(xˆi)+yˆj2π(x2+y2)Cμ0I(xˆj)−yˆi2π(x2+y2)Dμ0I(yxˆi)−yˆj2π(x2+y2)
Four particles enter a region of uniform magnetic field. Their trajectories are shown in figure. What are the signs of the charge of all four particles ?
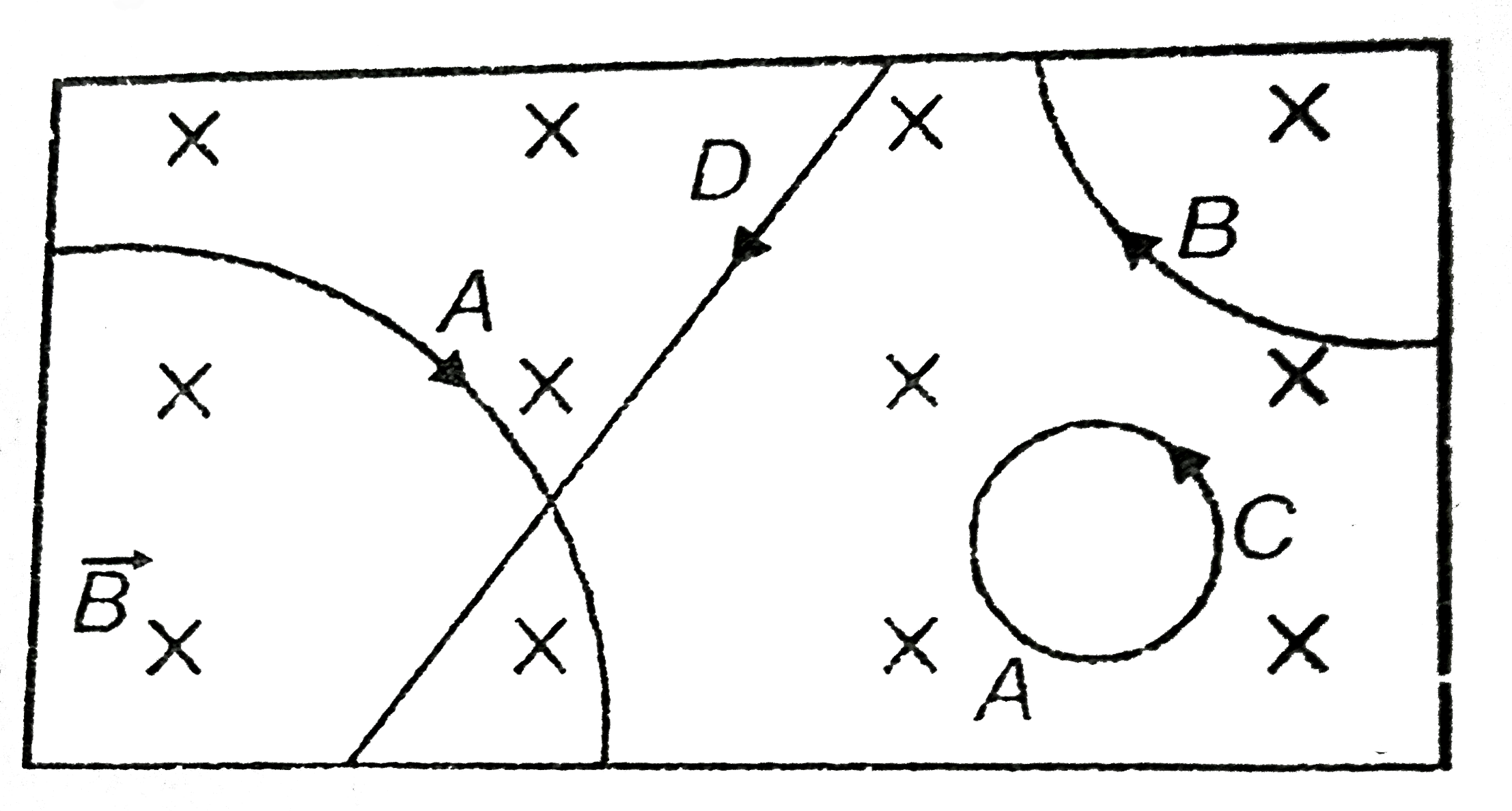
View SolutionA long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field B at a point having coordinate (x,y) on the z=0 plane is:
View SolutionIf a charged particle enters perpendicular in the uniform magnetic field then
View SolutionA charged particle enters in a uniform magnetic field with a certain velocity. The power delivered to the particle by the magnetic field depends on
View SolutionIn a region where both non-zero uniform electric field and magnetic field coexist, the path of a charged particle
View Solution