A loop ABCD containing two resistors as shown in figure is placed in a uniform magnetic fielf B directed outwards to the plane of page. A sliding conductor EF of length l and of negligible resistance moves to th right with a uniform velocity v as shown in Fig. Determine the current in each branch.
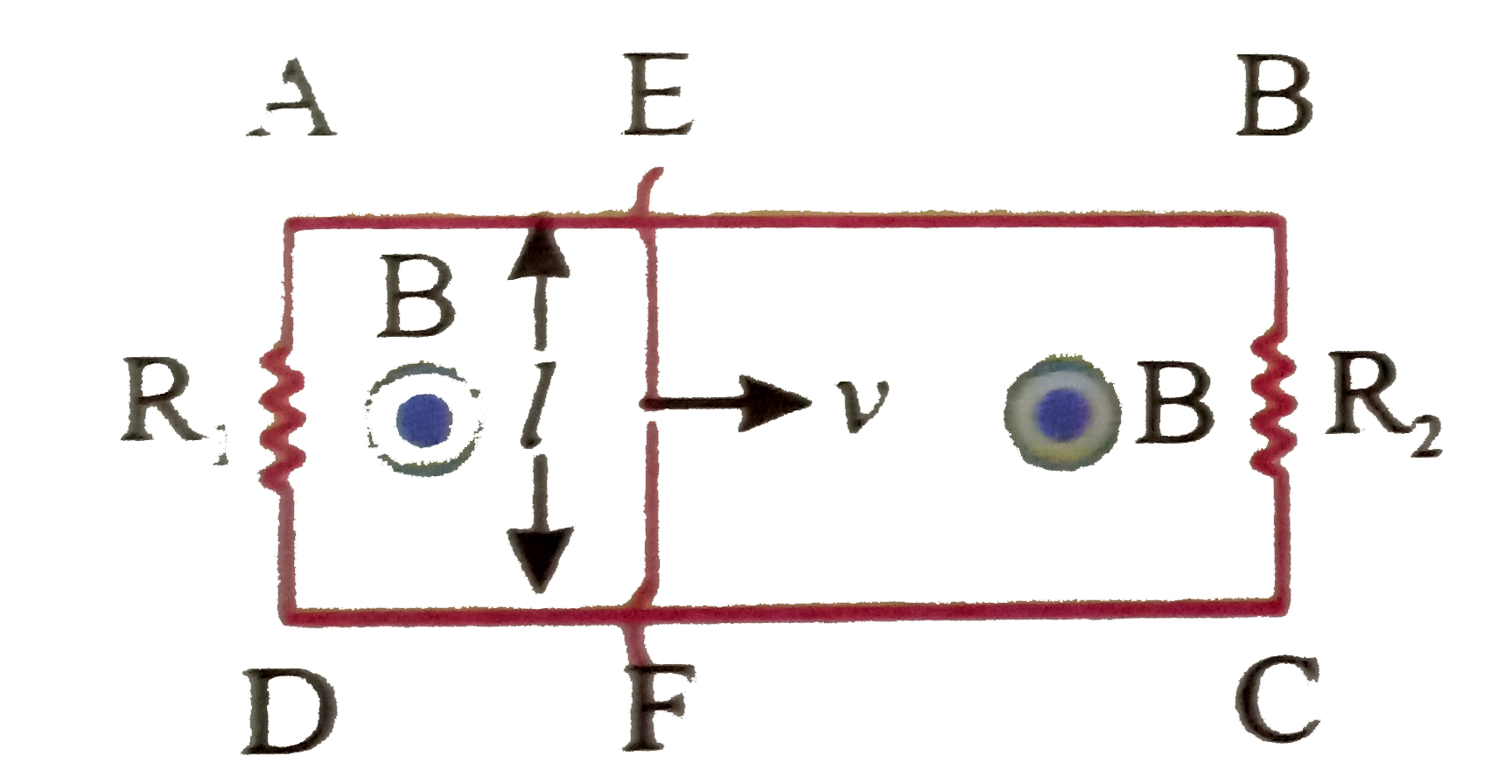
The magnetic field induction B, length l and the velocity v of the conductor EF are mutually perpendicular, hence the emf induction in it is e=Blv (with end F of the rod at higher potential)
∴ The effective electric circuit can be redrawn as shwon Fig.
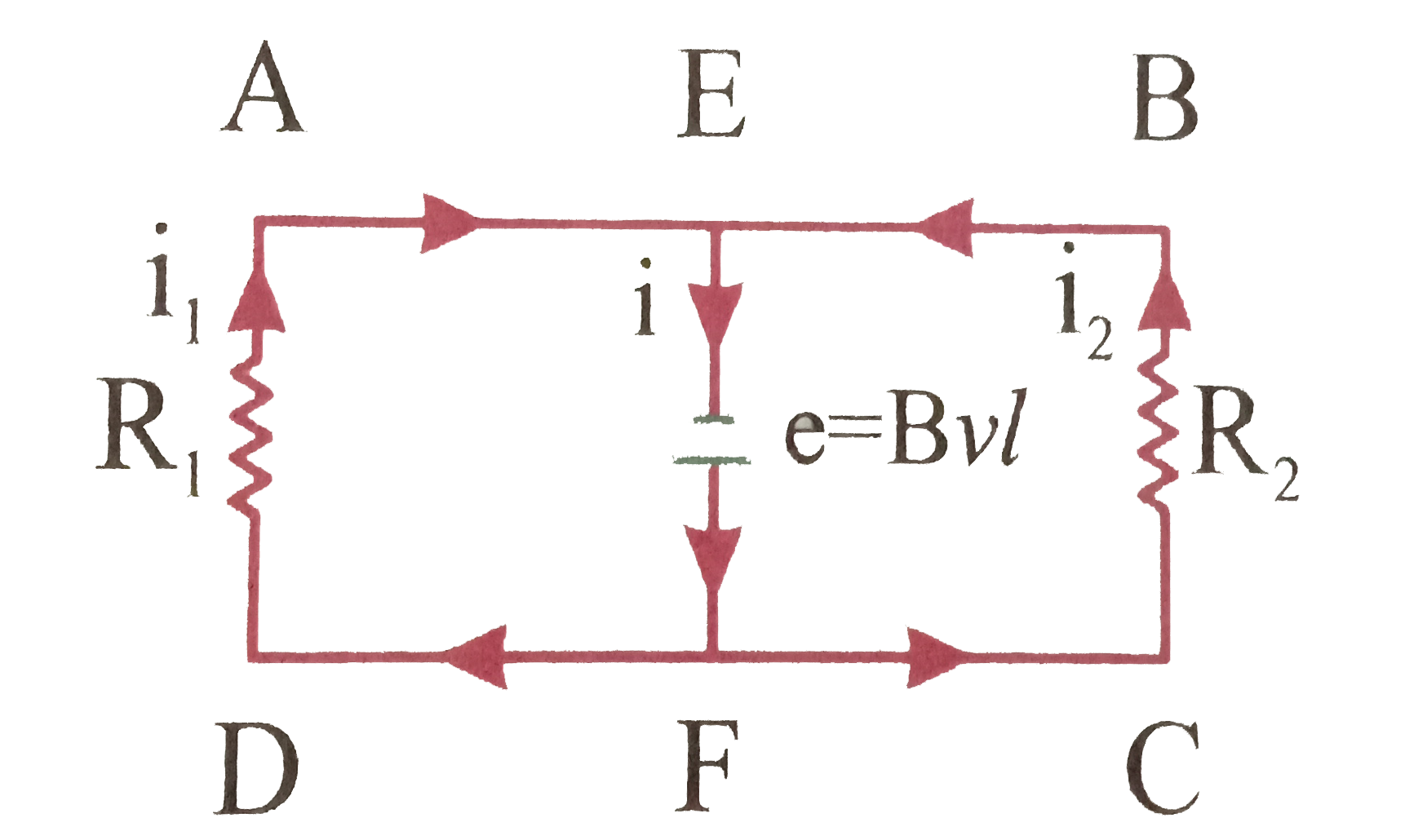
The resistance R1 and R2 are in parallel, so the equilvalent resistance R is given by 1R=1R1+1R2
From Ohms law, the total current i=eR
i=Blv(1R1+1R2)
Current in AD is i1=BlVR1, current in BC is
i2=BlVR2
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - C.U.Q 151videos
ELECTRO MAGNETIC INDUCTION
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Assertion & Reason11videos
ELECTRO MAGNETIC INDUCTION
- BOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -443videos
ELECTRIC CHARGES AND FIELDS
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - LEVEL-II(H.W)14videos
ELECTRO MAGNETIC WAVES
Similar Questions
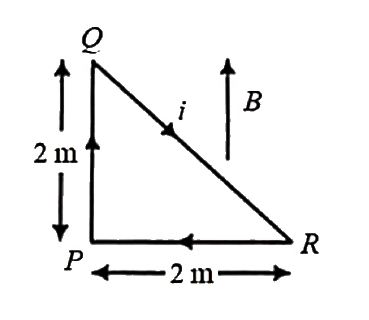
A loop PQR carries a current i=2A as shown in the figure. A uniform magnetic field B = 2T exists in space parallel to the plane of the loop . The magnetic torque on the loop is
 View Solution
View SolutionA closed loop with the geometry shown in Fig. 3.9 is placed in a uniform magnetic field direction into the plane of the paper. If the magnetic field decreases with time, determine the direction of the induced emf in this loop.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A wire is bent to form the double loop shown in figure. There is a uniform magnetic field directed into the plane of the loop. If the magnitude of this field is decreasing, current will flow from:
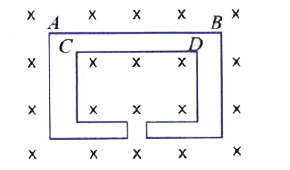 AA to B and C to DBB to A and D to CCA to B and D to CDB to A and C to D
AA to B and C to DBB to A and D to CCA to B and D to CDB to A and C to D - Question 2 - Select One
A wire is bent to form the double loop shown in figure. There is a uniform magnetic field directed into the plane of the loop. If the magnitude of this field is decreasing current will flow from:
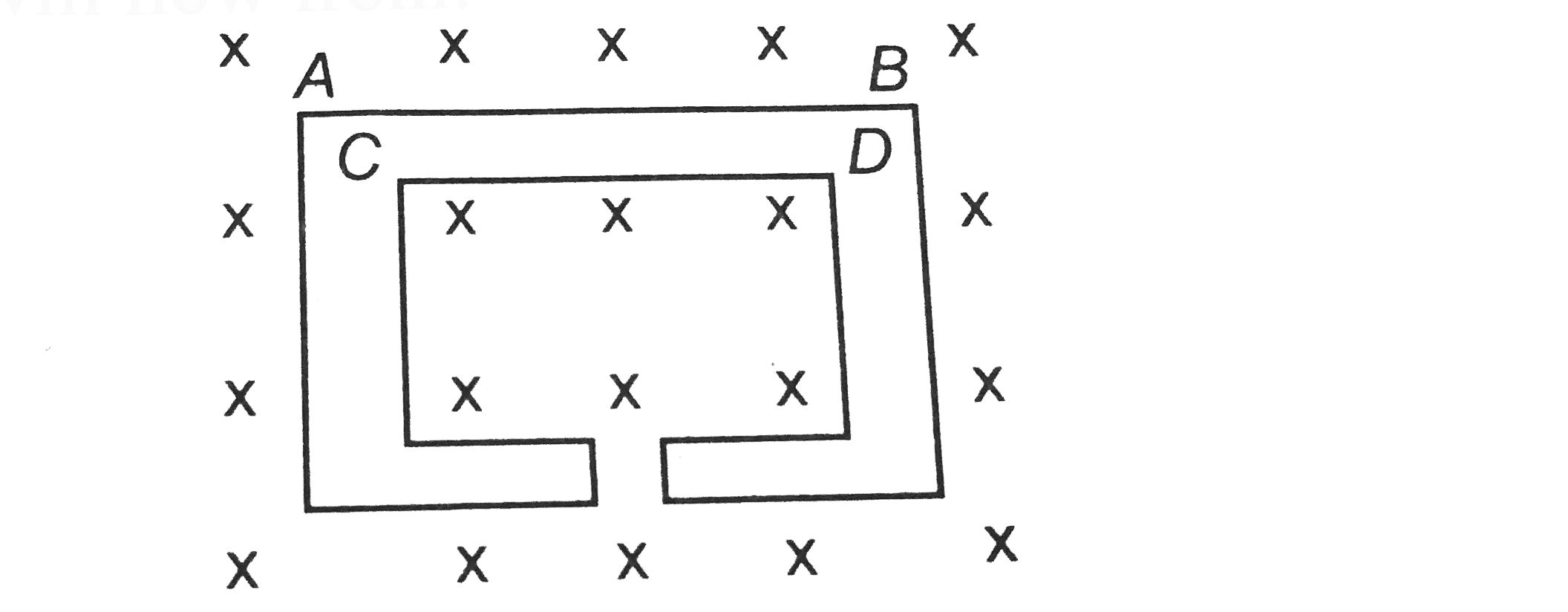 AA to B and C to DBB to A and D to CCA to B and D to CDB to A and C to D
AA to B and C to DBB to A and D to CCA to B and D to CDB to A and C to D - Question 3 - Select One
A square loop of side L, resistance R placed in a uniform magnetic field B acting normally to the plane of the loop. If we attempt to pull it out of the field with a constant velocity v, then the power needed is
ABRlvBB2l2v2RCBl2v2RDBvlR
In the figure shown as uniform magnetic field |B|=0.5T is perpendicular to the plane of circuit. The sliding rod of length l=0.25m moves uniformly with constant speed v=4ms−1. If the resistance of the sllides is 2Ω, then the current flowing through the sliding rod is
 View Solution
View SolutionA long conducting wire AH is moved over a conducting triangular wire CDE with a constant velocity v in a uniform magnetic field →B directed into the plane of the paper. Resistance per unit length of each wire is ρ. Then
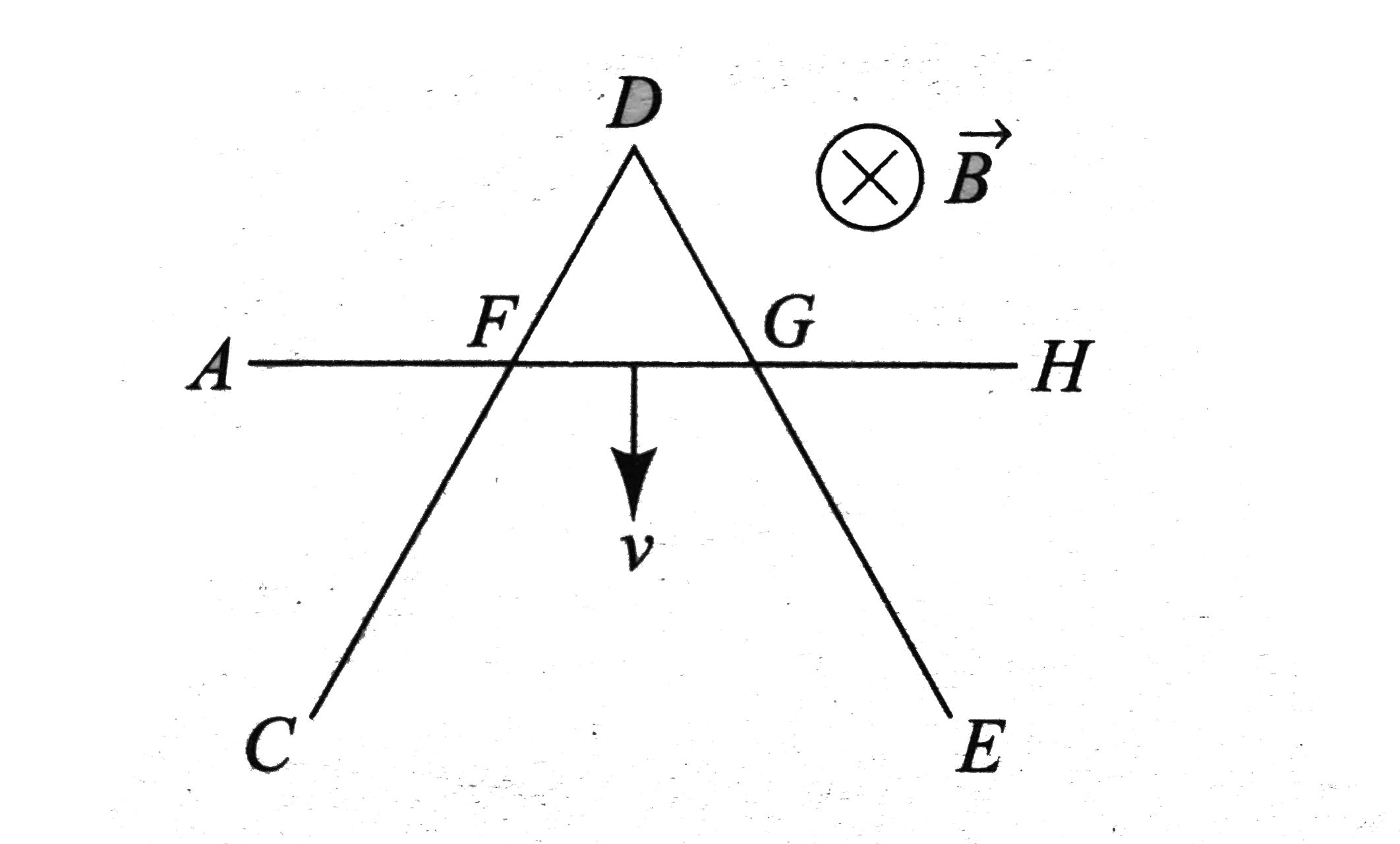 View Solution
View SolutionA wire is bent in the form of a V shape and placed in a horizontal plane. There exists a uniform magnetic field B perpendicular to the plane of the wire. A uniform conducting rod starts sliding over the V shaped wire with a constant speed v as shown in the figure. If the wire no resistance, the current in rod wil
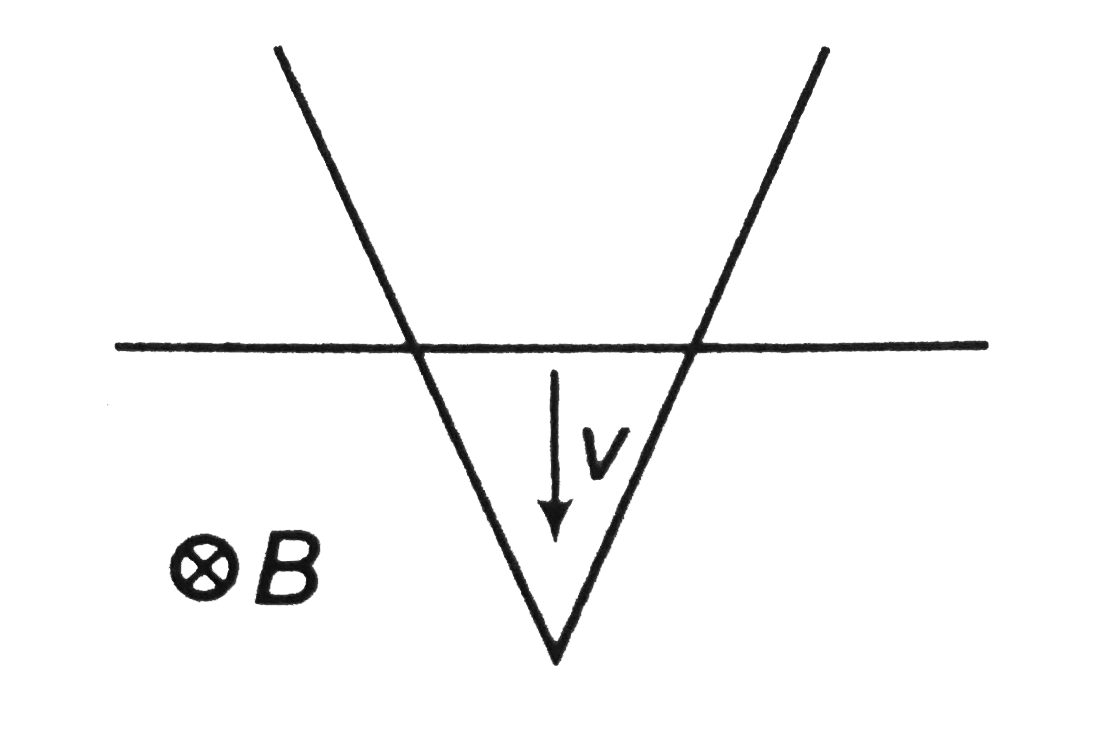 View Solution
View SolutionA square loop is placed in a uniform magnetic field →B as shown in fig. The power needed to pull it out of the field with a velocity v is proportional to
 View Solution
View SolutionA circular loop carrying a current I is placed in the xy-plane as shown in figure. A uniform magnetic fied B is oriented along the positive z-axis. The loop tends to
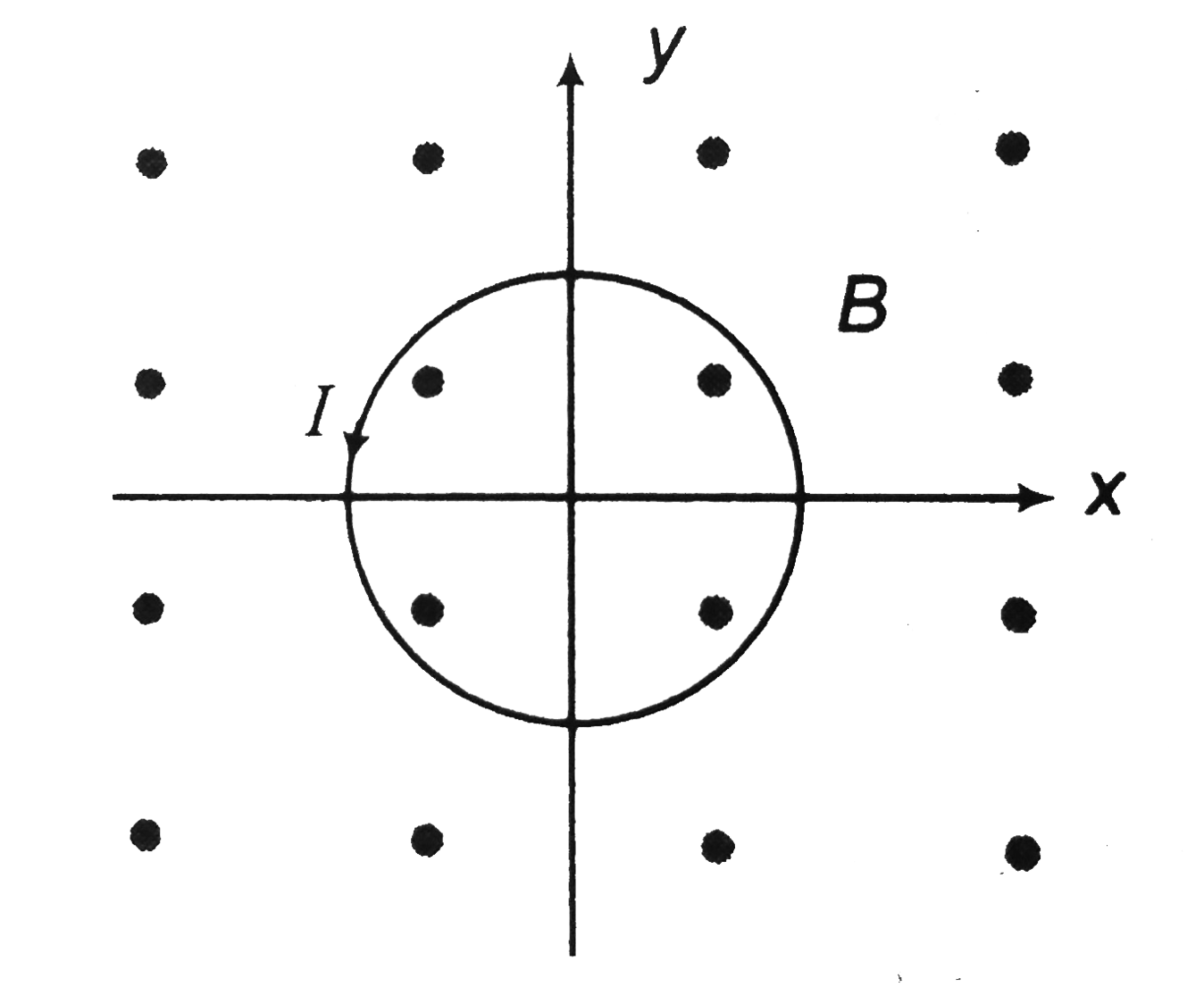 View Solution
View Solution

