A small square loop of wire of side l is placed inside a large square loop of wire of side L(L>>l). The loops are coplanar and their centre coincide. What is the mutual inductance of the system ?
Considering the large loop to be made up of four rod each of length L, the field at the centre, i.e., at a distance (L/2) from each rod, will be
B=4×μ04πId[sinα+sinβ]
i.e., B=4×μ04πI(L/2)×2sin45
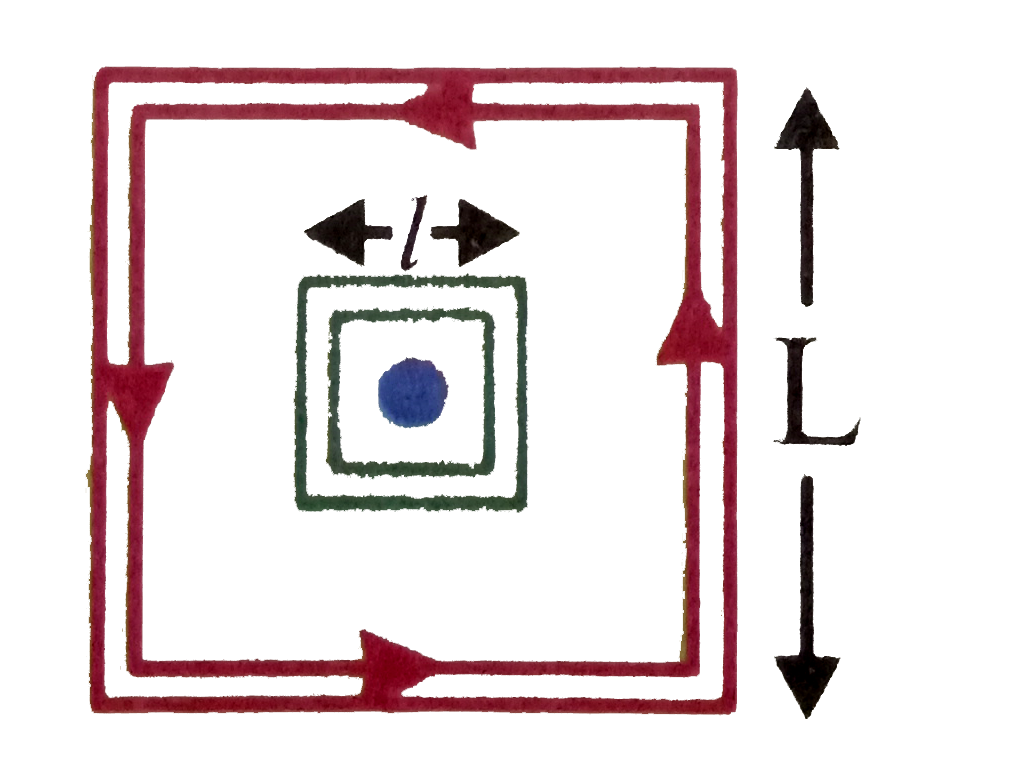
i.e., B1=μ04π8√2LI
So the flux linked with smaller loop
ϕ2=B1S2=μ04π8√2Ll2
and hence, M=ϕ2I=2√2μ0πl2L⇒M∝l2L
Topper's Solved these Questions
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - C.U.Q 1
51 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Assertion & Reason
11 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -4
43 Videos
- ELECTRO MAGNETIC WAVESBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - LEVEL-II(H.W)
14 Videos
Similar Questions
A small square loop of wire of side l is placed inside a large squre loop of wire of side L(>>l). The loops are coplanar and their centre coincide. What is the mutual inductance of the system ?
View SolutionA small square loop of wire of side l is placed inside a large square loop of wire of side (L>>l). The loops are coplanar and their centres coincide. If the mutual inductance of the system is p√qμ0πl2L, then find (p+q).
View Solution
Knowledge Check
A small square loop of wire of side l is placed inside a large square loop of wire of side L(L>>l). The loops are co-planer and their centres coincide. The mutual inductance of the system is proportional to
AlLBl2LCLlDL2lA square loop of side L carries a current I. Another smaller square loop of side l(l<<L) carrying a current i is placed inside the bigger loop such that they are coplanar with their centre coinciding. If the currents in the loops are in the same direction, the magnitude of the torque on the smaller loop is
Aμ0Iil2√2πLBμ0Iil22πLCμ0Iil2√32πLDZero
A small square loop of wire of side l is placed inside a large square loop of wire of side L(L>>l) .The loops are coplanar and their centers coincide.The mutual inductance of the system is proportional to
View SolutionA small square loop of wire of side I is placed inside a large square loop of wire of side L(L>> ) .The loops are coplanar and their centers coincide.The mutual inductance of the system is proportional to
View SolutionA small square loop of wire of side I is placed inside a large square loop of wire of side L(L>> I ) .The loops are coplanar and their centers coincide. The mutual inductance of the system is proportional to
View SolutionA small circular loop of radius a is placed inside a large square loop of edge L(>>a) . The loops are coplanar and concentric. Find mutual inductance.
View SolutionA small square loop of side 'a' and one turn is placed inside a larger square loop of side b and one turn (b>>a). The two loops are coplanar with their centres coinciding. If a current I is passed in the square loop of side 'b', then the coefficient of mutual inductance between the two loops is :
View SolutionA circular loop of radius r is placed at the center of current carrying conducting square loop of side a. If both loops are coplanar and a >> r, then the mutual inductance between the loops will be
View Solution
