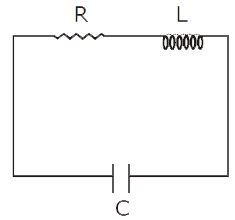
An LCR curcuit is equivalent to a damped pendulum. In an LCR circuit the capacitor is charged to and then connected to the L ans R as shown below.
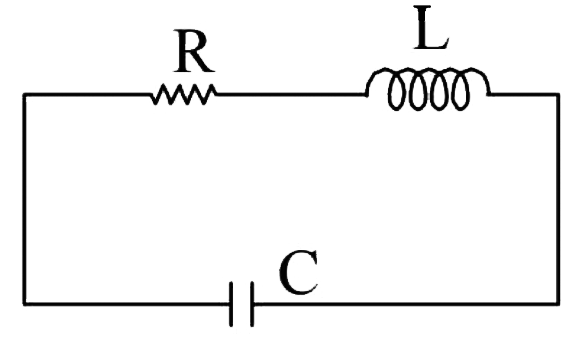
If a student plaots graphs of the square of maximum charge on the capacitor with time (t) for two different values of L then which of the following represents this graph correclty? (plots are schematic and not drawn to scale).
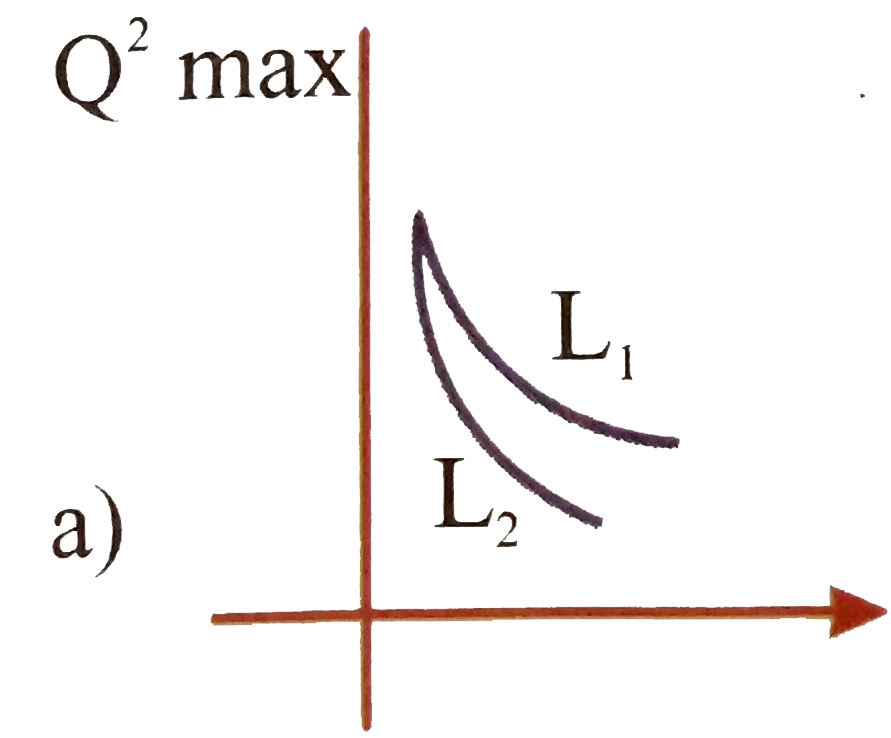
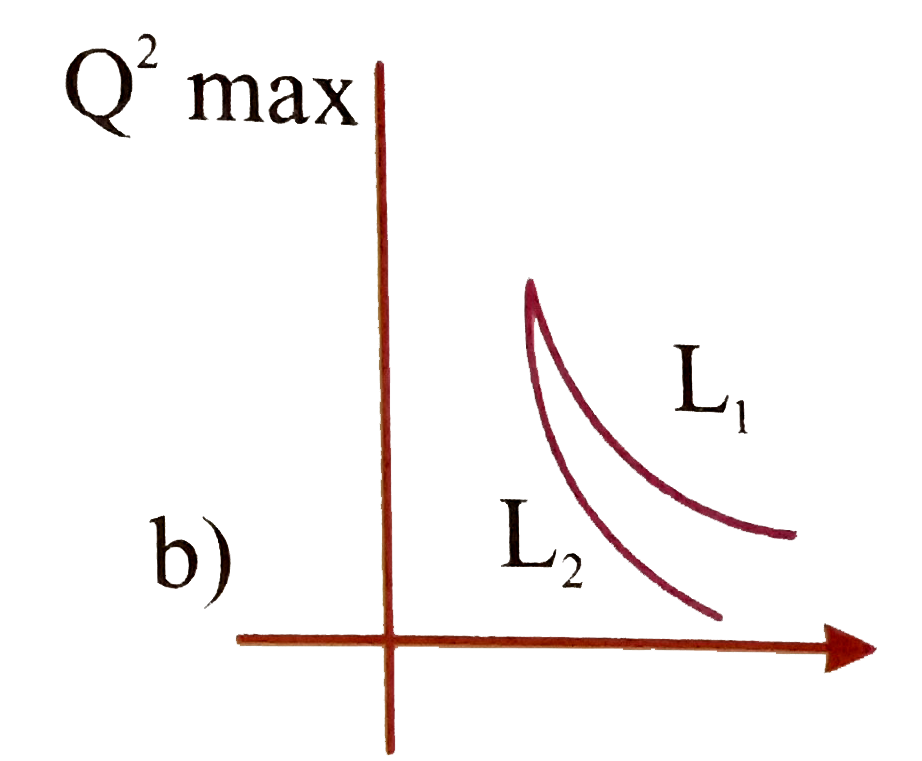
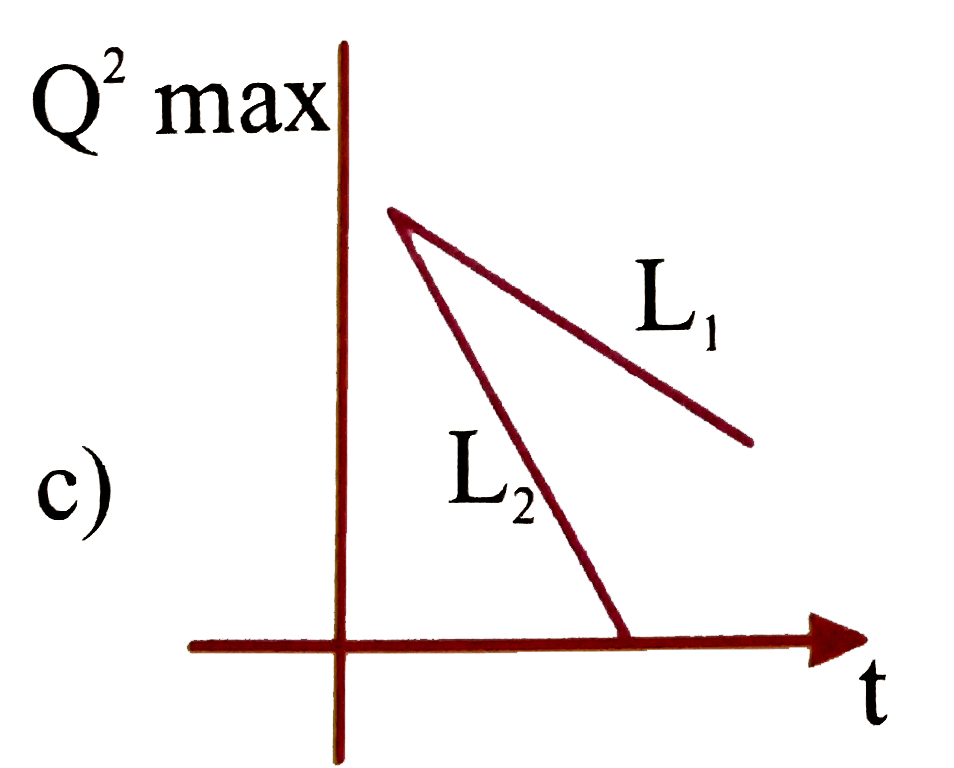

The correct Answer is:A
For a demped pendulum,
(Since plays the same role as )
Topper's Solved these Questions
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - NCERT Based Questions
10 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Single Answer Questions Level -V
11 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Level-II (C.W)
28 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -4
43 Videos
- ELECTRO MAGNETIC WAVESBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - LEVEL-II(H.W)
14 Videos
Similar Questions
The voltage-current graphs for two resistor of the same material and the same radius with lengths, L1andL2 are shown in fig 5.2. if L1>L2, state with reason which of these graphs represents voltage- current change of L1.

View SolutionIn the circuit shown in the figure, if both the lamps L1 and L2 are identical
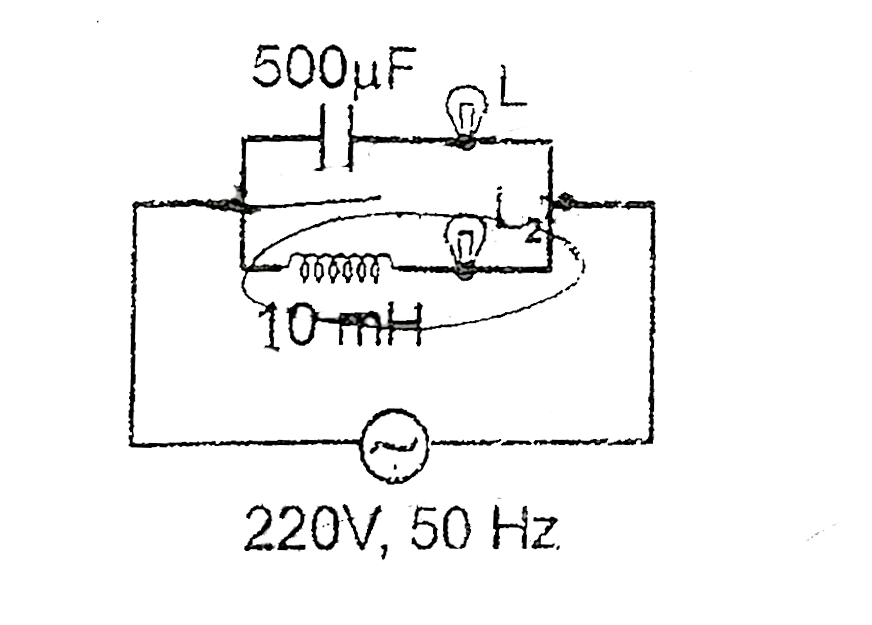
View Solution
Knowledge Check
An LCR circuit is equivalent to a damped pendulum In an LCR circuit the capacitor is charged to Q0 and then connected to the L and R as shown below : Thus potential energy stored in the capacitor and that in the inductor also oscillates between maximum value an zero with double the frequency.
If a student plots graphs of the square of maximum charge (Q2max) on the capacitor with time (t) for two different values L1andL2(L1>L2) of L then which of the following reprersent this graph correctly ? (Plots are shematic and not drawn to scale )A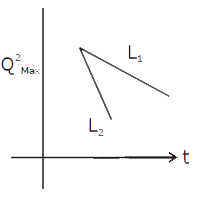 B
B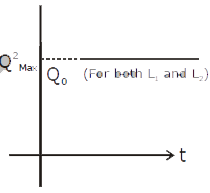 C
C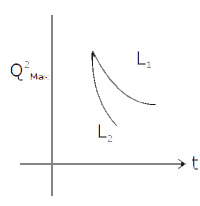 D
D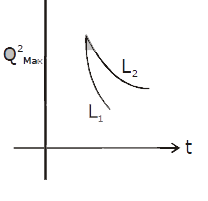
In an LC circuit the capacitor has maximum charge q0. The value of (dIdt)max is
 Aq0LCBq0√LCCq0LC−1Dq0LC+1
Aq0LCBq0√LCCq0LC−1Dq0LC+1In LCR circuit, capacitor C is changed to 4C, then what should be the value of L to keep resonance frequency same
A2 LBL/2CL/4D4L
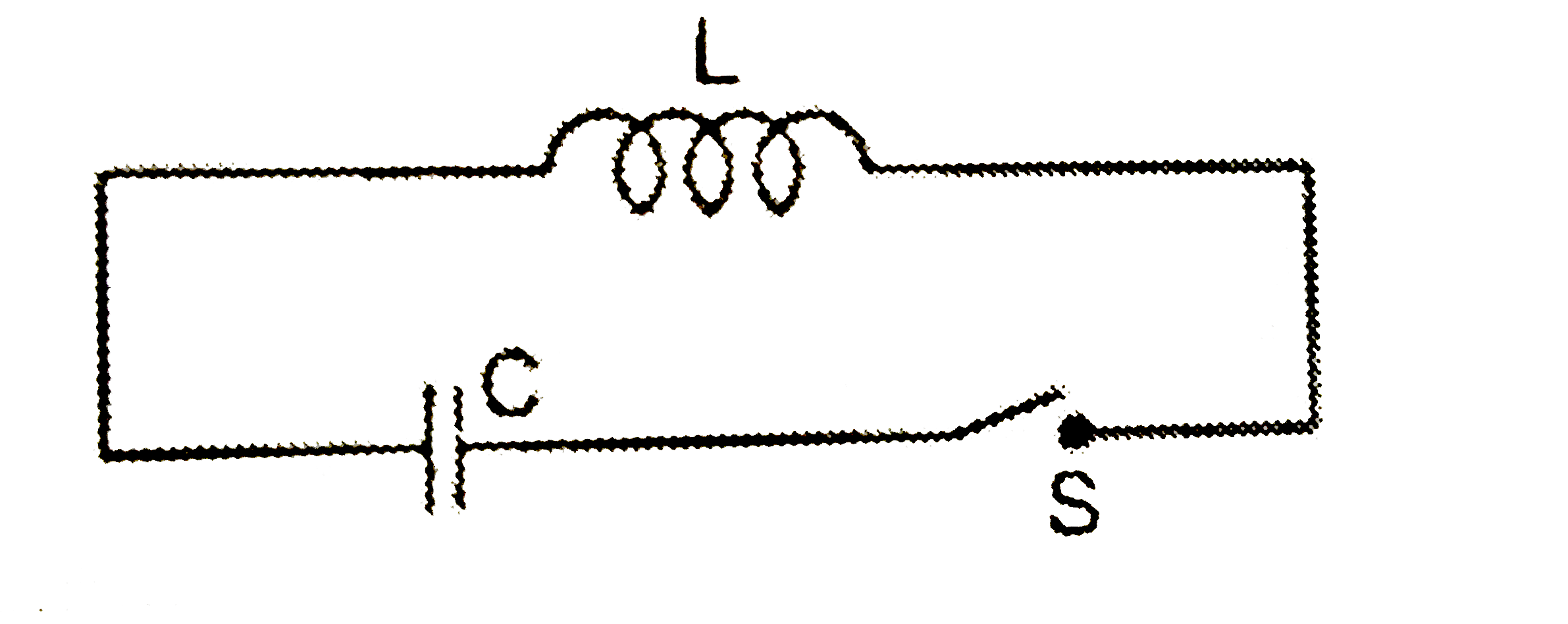
The capacitor of capacity C is given charge Q and then connected to the coil of inductance L by closing the switch S. The maximum current flowing in the circuit at any later time will be
View SolutionThe current in an L - R circuit in a time t = 2L / R reduces to-
View SolutionWhen a capacitor is charged then
lc= conduction current ld = displacembet current)
View SolutionA capacitor of capacitance C is given charge Q and then connected in parallel to a coil of inductance L. There is no resitance in the circuit. When the charge on the capacitor becomes zero, the current in the coil will be
View SolutionThe graph between L and T2 is
View Solution
