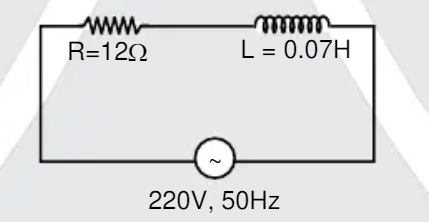
In the given circuit assuming inductor and source to be ideal, the phase differece between current I1 and I2 :
tan−1(XCR)−π2
tan−1(XCR)
tan−1(XCR)+π2
π2
The correct Answer is:C
Let : Vs=Vssinωt
I1=I0sin(ωt−π/2),I2=I02sin(ωt+θ)
tanθ=XCR
So phase difference =θ+π2,tan−1(XcR)+π2
Topper's Solved these Questions
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - I (H.W)
Explore 23 Videos
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - II(H.W)
Explore 13 Videos
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - V
Explore 83 Videos
- ATOMIC PHYSICSBook:NARAYNAChapter:ATOMIC PHYSICSExercise:LEVEL-II (H.W)
Explore 14 Videos
Similar Questions
Knowledge Check
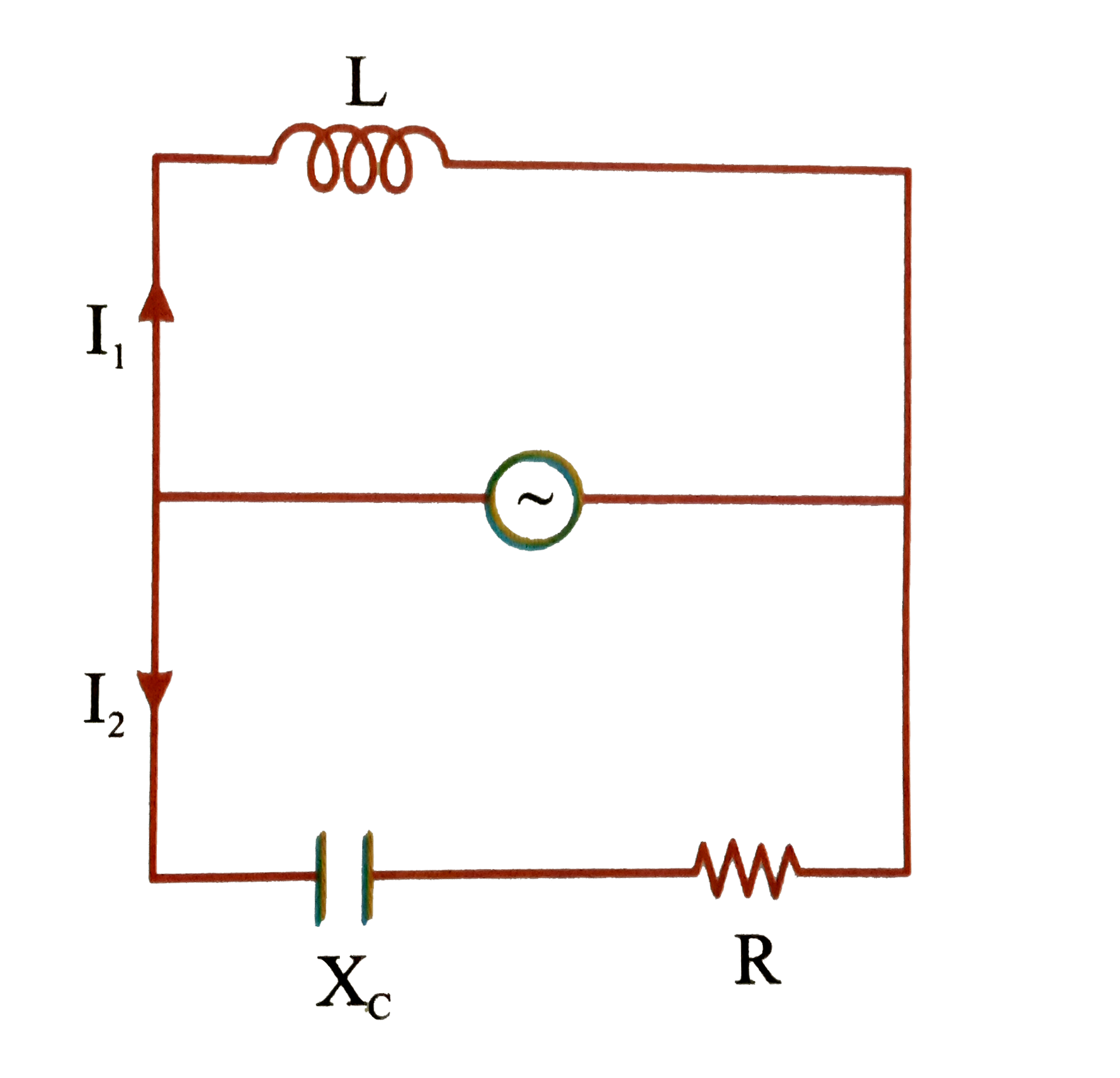
In the shown AC circuit phase different between current I1 and I2 is
 Aπ2−tan−1xLRBtan−1(xL−xC)RCπ2+tan−1xLRDtan−1(xL−xC)R+π2
Aπ2−tan−1xLRBtan−1(xL−xC)RCπ2+tan−1xLRDtan−1(xL−xC)R+π2In the given circuit currents I1 and I2 are
 .A107A,127AB−27A,125AC87A,125AD87A,127A
.A107A,127AB−27A,125AC87A,125AD87A,127AIn the given circuit the current I1 is
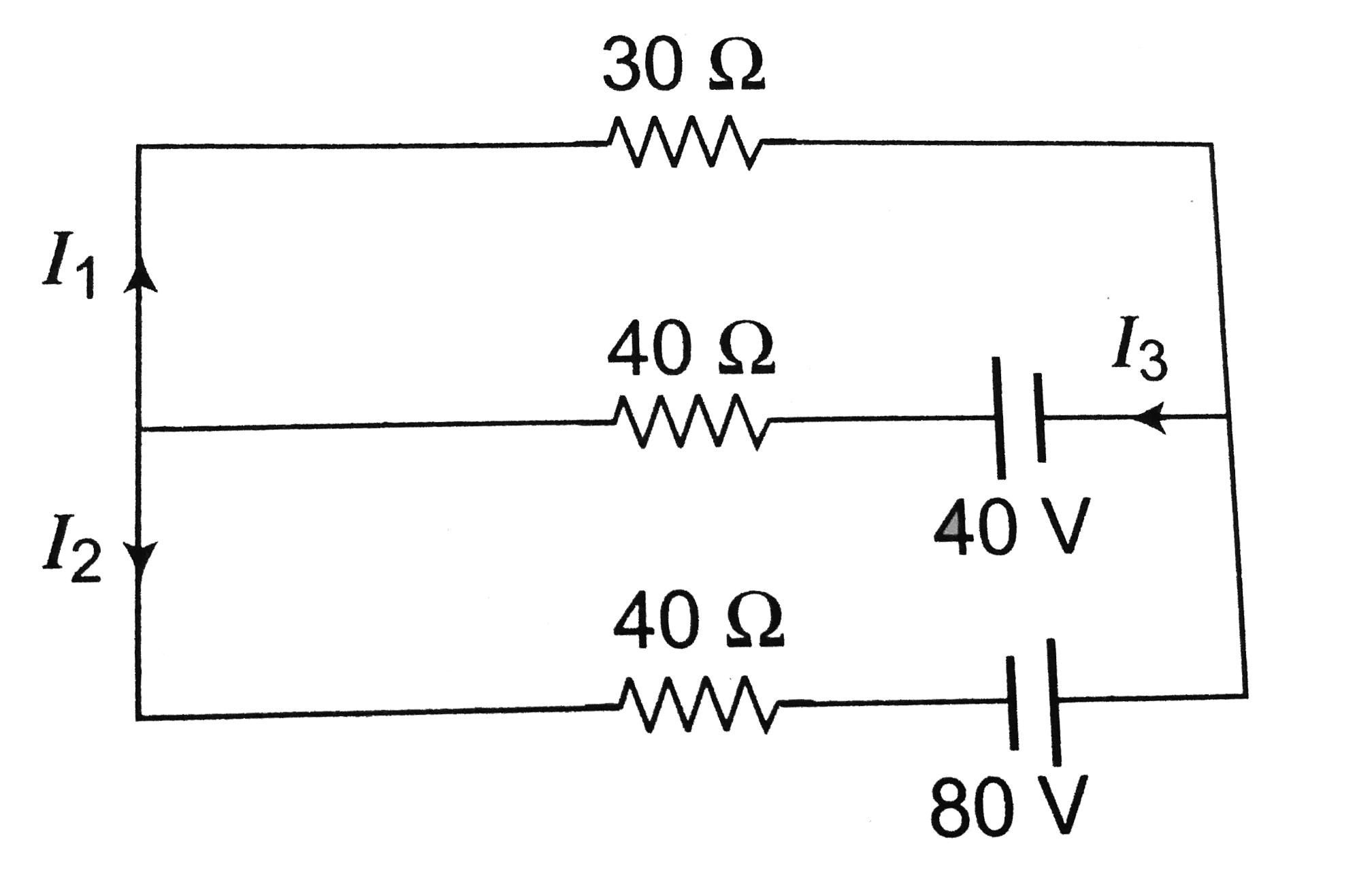 A0.4AB−0.4AC0.8AD−0.8A
A0.4AB−0.4AC0.8AD−0.8A
In the circuit shown in Fig. (i) find the phase difference between the currents through L and R1
(ii) find the phase difference between potential differece across C and R2
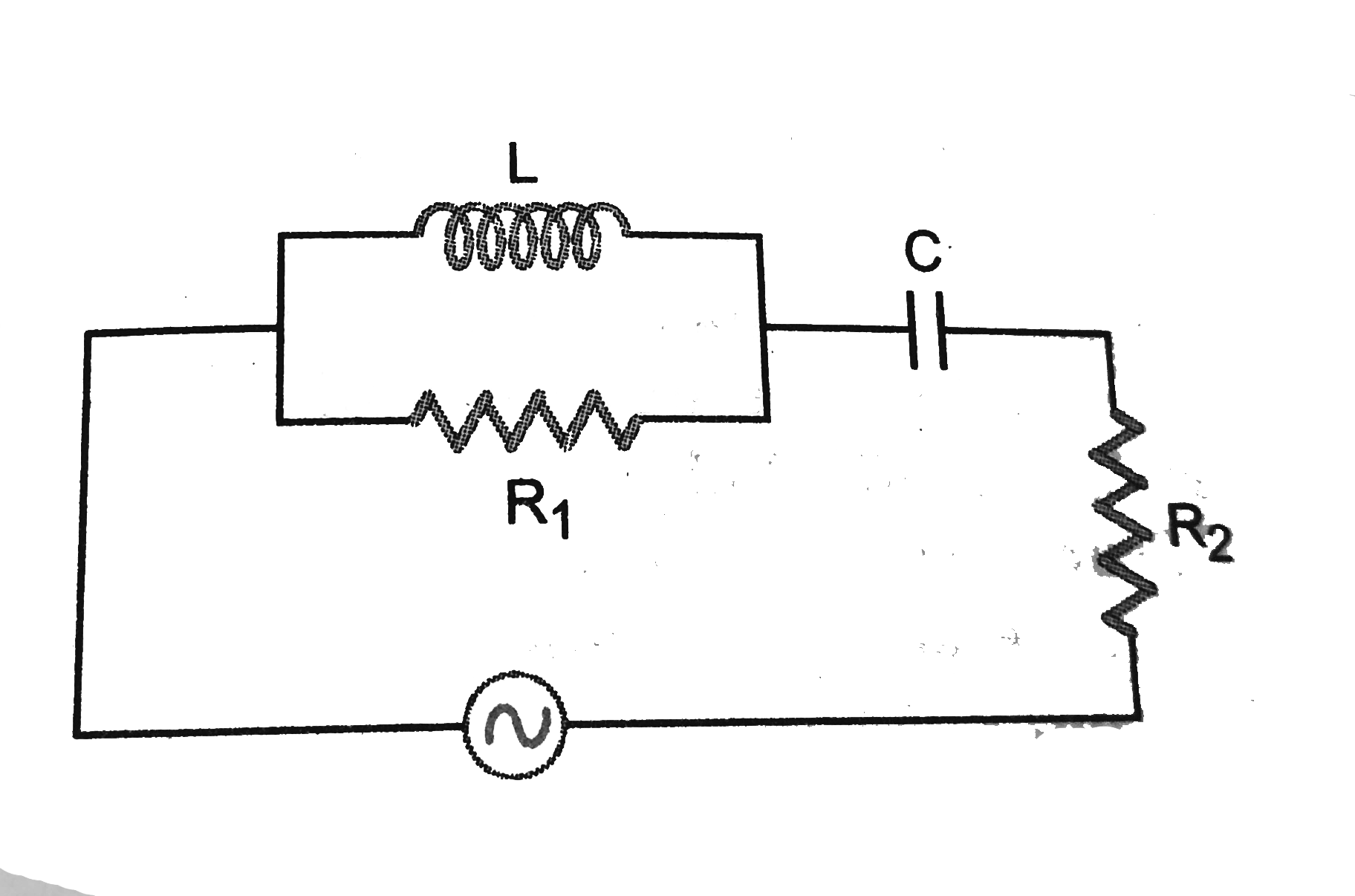
View SolutionIn the circuit shown, the currents i1 and i2 are
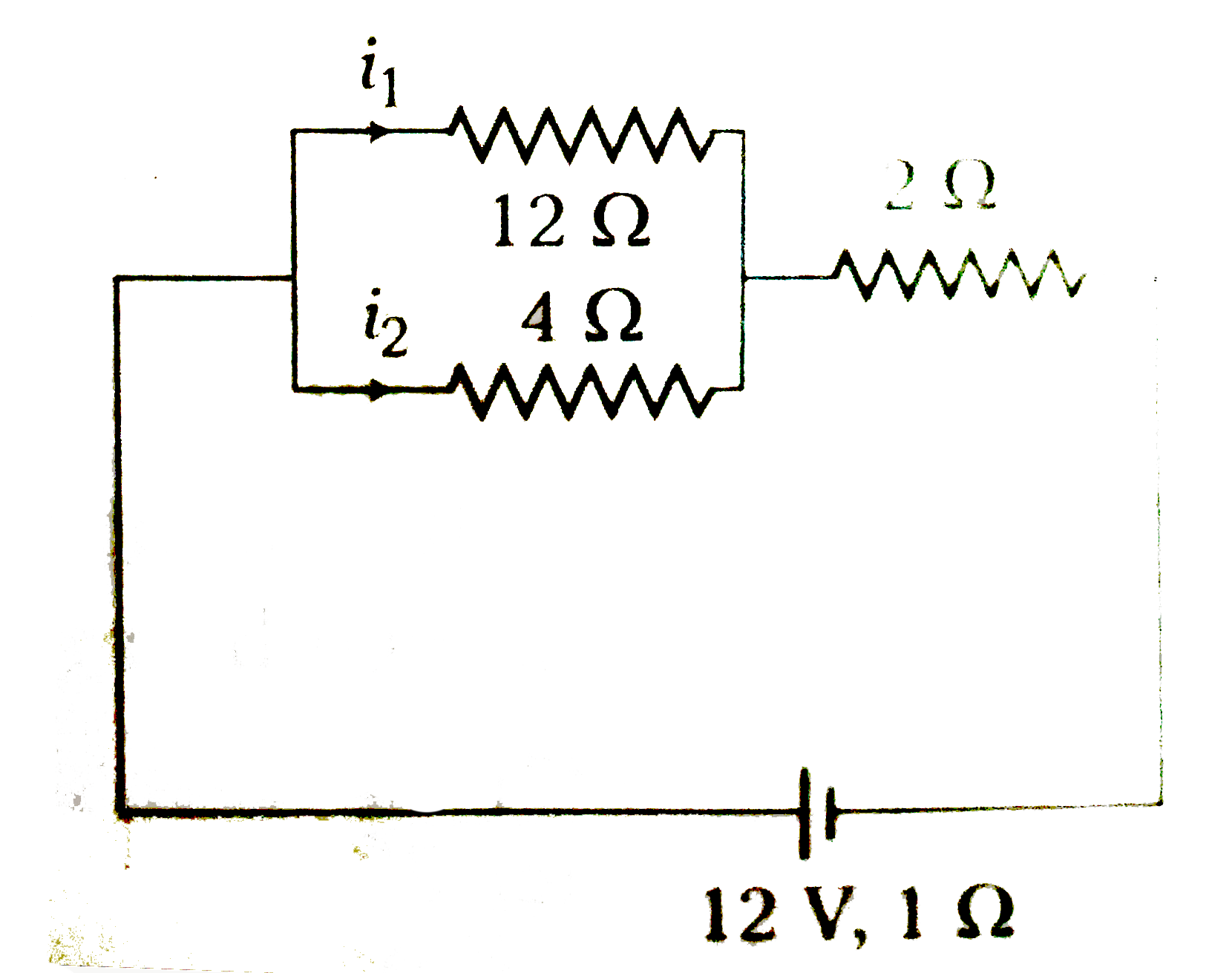
View SolutionIn the circuit shown in figure :
R=10Ω,L=√310H,R2=20Ω and C=√32mF. Current in L−R1 circuit is I1 in C−R1 circuit is I2 and the main current is I

Phase difference between I1 and I2 is
View SolutionAn L-C-R circuit is connected to a source of A.C. current. At resonance, the phase difference between the applied voltage and the current in the circuit, is
View SolutionAn inductor (L) and resistance (R) are connected in series with an AC source. The phase difference between voltage (V) and current (i) is 45∘. Now a capacitor (C) is connected in series with L-R, If the phase difference between V and i remain same, then capacitive reactance and impedance of L-C-R circuit will be-
View Solution