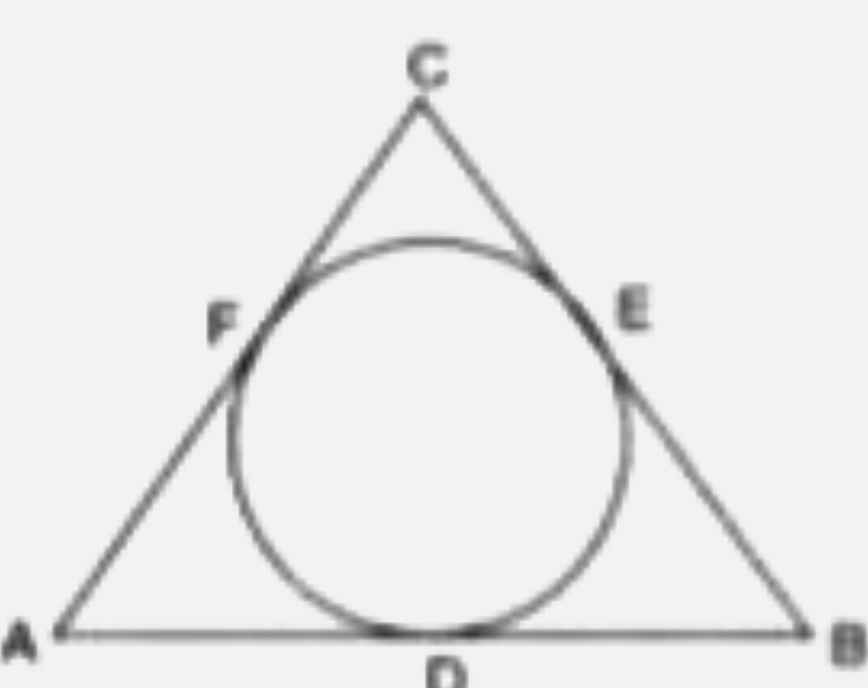
In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F respectively. If AB= 12 cm, BC= 8 cm and AC = 10 cm, find the lengths of AD, BE and CF.
To solve the problem, we need to find the lengths of segments AD, BE, and CF in triangle ABC with the given side lengths.
1. Identify the given values:
- AB = 12 cm
- BC = 8 cm
- AC = 10 cm
2. Define the segments:
- Let AD = x
- Let BE = y
- Let CF = z
3. Express the sides in terms of x, y, and z:
- From triangle ABC, we can express the sides as:
- AB = AD + BD → 12 = x + y
- BC = BE + CE → 8 = y + z
- AC = CF + FA → 10 = z + x
4. Set up the equations:
- From the first equation:
x+y=12 (Equation 1)
- From the second equation:
y+z=8 (Equation 2)
- From the third equation:
z+x=10 (Equation 3)
5. Add all three equations:
(x+y)+(y+z)+(z+x)=12+8+10
Simplifying this gives:
2x+2y+2z=30
Dividing by 2:
x+y+z=15(Equation4)
6. Subtract Equation 1 from Equation 4:
(x+y+z)−(x+y)=15−12
This simplifies to:
z=3
7. Subtract Equation 2 from Equation 4:
(x+y+z)−(y+z)=15−8
This simplifies to:
x=7
8. Subtract Equation 3 from Equation 4:
(x+y+z)−(z+x)=15−10
This simplifies to:
y=5
9. Final values:
- AD (x) = 7 cm
- BE (y) = 5 cm
- CF (z) = 3 cm
Conclusion:
The lengths of the segments are:
- AD = 7 cm
- BE = 5 cm
- CF = 3 cm
- AB = 12 cm
- BC = 8 cm
- AC = 10 cm
- Let AD = x
- Let BE = y
- Let CF = z
- From triangle ABC, we can express the sides as:
- AB = AD + BD → 12 = x + y
- BC = BE + CE → 8 = y + z
- AC = CF + FA → 10 = z + x
- From the first equation:
x+y=12 (Equation 1)
- From the second equation:
y+z=8 (Equation 2)
- From the third equation:
z+x=10 (Equation 3)
(x+y)+(y+z)+(z+x)=12+8+10
Simplifying this gives:
2x+2y+2z=30
Dividing by 2:
x+y+z=15(Equation4)
(x+y+z)−(x+y)=15−12
This simplifies to:
z=3
(x+y+z)−(y+z)=15−8
This simplifies to:
x=7
(x+y+z)−(z+x)=15−10
This simplifies to:
y=5
- AD (x) = 7 cm
- BE (y) = 5 cm
- CF (z) = 3 cm
The lengths of the segments are:
- AD = 7 cm
- BE = 5 cm
- CF = 3 cm
Topper's Solved these Questions
Similar Questions
In the given figure, AB, BC and CA are tangents to the given circle. If AB= 12cm, BC= 8cm and AC= 10cm, find the length of AD,BE=CF
View SolutionThe incircle of an isoceles triangle ABC, with AB=AC, touches the sides AB,BC and CA at D,E and F respecrively. Prove that E bisects BC.
View SolutionAP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC = 4 cm, then the length of AP (in cm) is
View SolutionAP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC = 4 cm, then the length of AP (in cm) is
View SolutionΔABC is right-angled at C. If AC=5cmandBC=12cm find the length of AB.
View SolutionIn ΔABC,∠ABC=∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
(ii) Find the length of BC and CD.
View SolutionIn triangle ABC, ∠B=90∘ and tan A = 0.75 If AC = 30 cm, find the lengths of AB and BC.
View SolutionIn triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC
View SolutionIn Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of side AD.
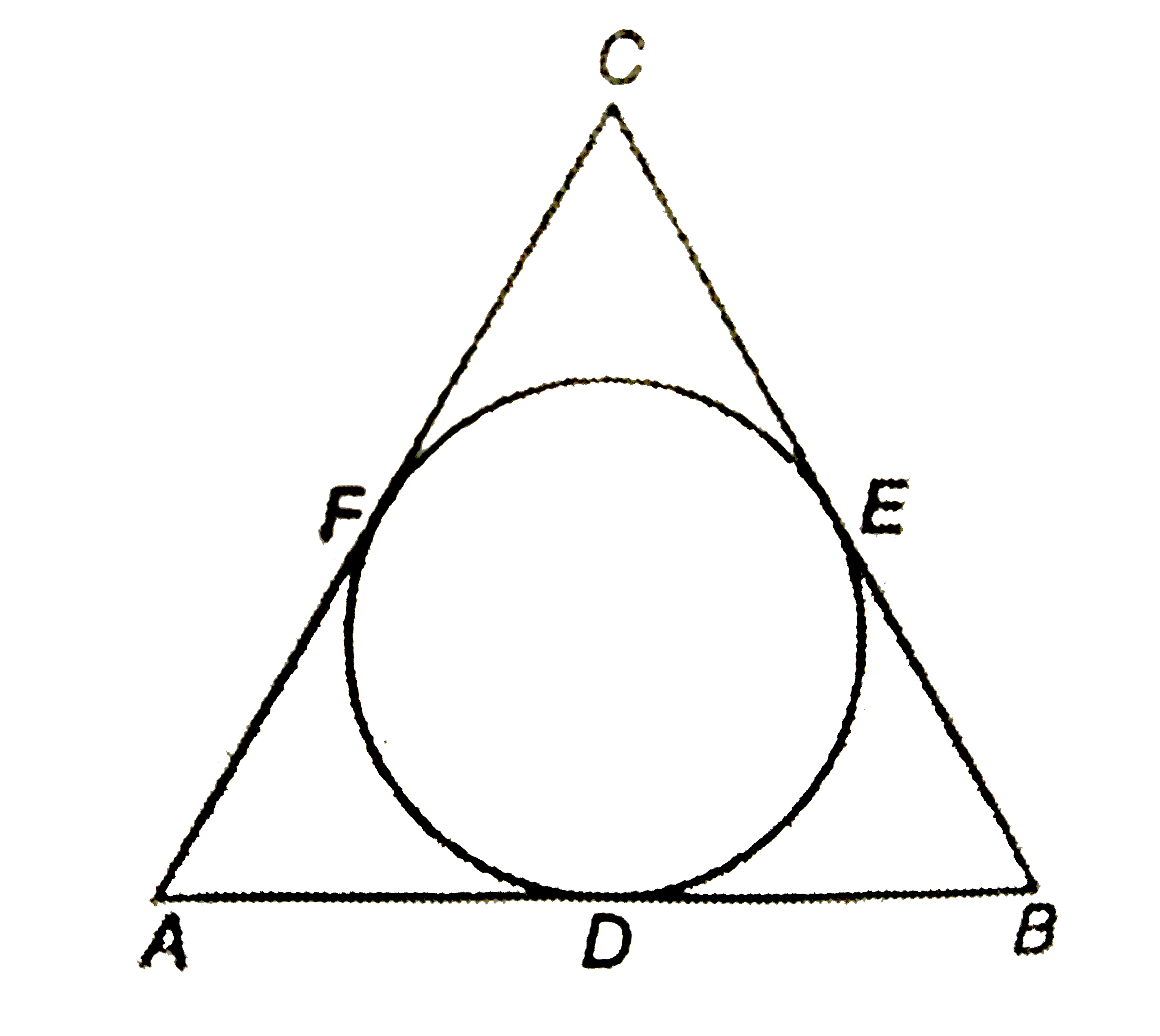
View SolutionA circle is inscribed in a △ABC having sides 8 cm, 10 cm and 12 cm as shown in figure. Find AD, BE and CF.
View Solution
