In the given figure, GH || IJ and AC ||BD. AB and CD are bisector of ∠EAHand∠FCJ respectively, find ∠ABD+∠BDC,if∠BAC=3∠BDC
Step by step video & image solution for In the given figure, GH || IJ and AC ||BD. AB and CD are bisector of /_EAH and /_FCJ respectively, find /_ABD + /_BDC, if /_BAC = 3/_BDC by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
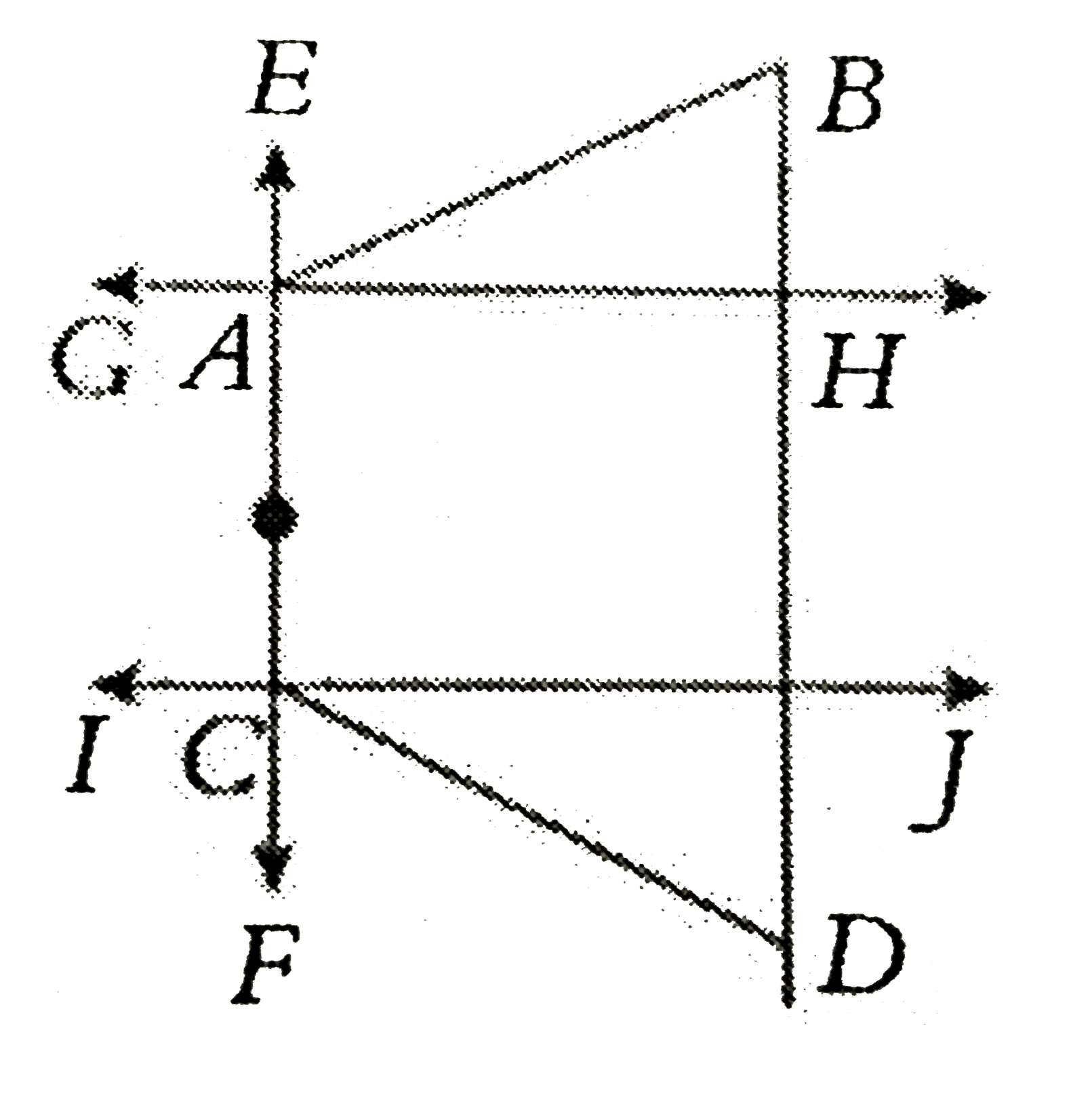
In the above figure, GH∣∣IJ and AC∣∣BD,AB and CD are bisectors of ∠EAH and ∠FCJ respectively. Find the ∠ABD+∠BDC, if ∠BAC=3∠BDC.
View SolutionIn the given figure if AC=BD then prove that AB=CD
View SolutionIn figure AD is the bisector of ∠BAC. If BD=2cm,CD=3cmandAB=5cm. Find AC :

View SolutionIn the given figure ∠ABD=∠BDC and CD=4AB. Show that BD=5BE.

View SolutionIn the given figure, if AC = BD, then prove that AB = CD.

View SolutionIn the given figure, if AC = BD, then prove that AB = CD.

View SolutionIn the given figure, D is a point on side BC of ΔABC such that BDCD=ABAC. Prove that AD is the bisector of ∠BAC.

View SolutionIn the given figure AC = BD, prove that AB = CD.

View Solution
