Form the pair of linear equations in the following problem, and find the solution graphically: 10 students of class X took part in Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
To solve the problem step by step, we will first form the pair of linear equations based on the information provided and then solve them graphically.
Step 1: Define Variables
Let:
- x = number of boys
- y = number of girls
Step 2: Form the First Equation
According to the problem, the total number of students (boys + girls) is 10. Therefore, we can write the first equation as:
x+y=10
Step 3: Form the Second Equation
The problem states that the number of girls is 4 more than the number of boys. This can be expressed as:
y=x+4
Rearranging this equation gives us:
x−y+4=0
This is our second equation.
Step 4: Write the Pair of Linear Equations
Now we have the following pair of linear equations:
1. x+y=10 (Equation 1)
2. x−y+4=0 (Equation 2)
Step 5: Solve the Equations Graphically
To solve these equations graphically, we need to plot them on a graph.
For Equation 1: x+y=10
- When x=0:
y=10
(Point A: (0,10))
- When y=0:
x=10
(Point B: (10,0))
For Equation 2: x−y+4=0 or x−y=−4
- When x=0:
−y=−4⟹y=4
(Point C: (0,4))
- When y=0:
x=−4
(Point D: (−4,0))
Step 6: Plot the Points and Draw the Lines
- Plot points A (0,10) and B (10,0) for the first equation and draw a line through them.
- Plot points C (0,4) and D (−4,0) for the second equation and draw a line through them.
Step 7: Find the Intersection Point
The solution to the system of equations is the point where the two lines intersect. By examining the graph, we find that the lines intersect at the point (3,7).
Step 8: Interpret the Solution
From our defined variables:
- x=3 (number of boys)
- y=7 (number of girls)
Final Answer
The number of boys who took part in the quiz is 3, and the number of girls is 7.
---
Let:
- x = number of boys
- y = number of girls
According to the problem, the total number of students (boys + girls) is 10. Therefore, we can write the first equation as:
x+y=10
The problem states that the number of girls is 4 more than the number of boys. This can be expressed as:
y=x+4
Rearranging this equation gives us:
x−y+4=0
This is our second equation.
Now we have the following pair of linear equations:
1. x+y=10 (Equation 1)
2. x−y+4=0 (Equation 2)
To solve these equations graphically, we need to plot them on a graph.
- When x=0:
y=10
(Point A: (0,10))
- When y=0:
x=10
(Point B: (10,0))
- When x=0:
−y=−4⟹y=4
(Point C: (0,4))
- When y=0:
x=−4
(Point D: (−4,0))
- Plot points A (0,10) and B (10,0) for the first equation and draw a line through them.
- Plot points C (0,4) and D (−4,0) for the second equation and draw a line through them.
The solution to the system of equations is the point where the two lines intersect. By examining the graph, we find that the lines intersect at the point (3,7).
From our defined variables:
- x=3 (number of boys)
- y=7 (number of girls)
The number of boys who took part in the quiz is 3, and the number of girls is 7.
Topper's Solved these Questions
Similar Questions
Form the pair of linear equations in the following problems, and find their solutions graphically.
10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
View SolutionForm the pair of linear equations in the following problems, and find their solutions graphically. (i) 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
View Solution
Knowledge Check
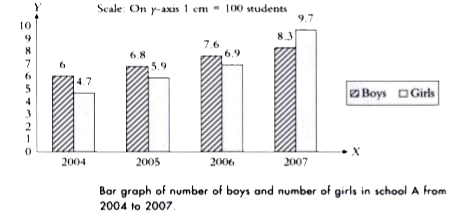
In which year the number of girls is more than the number of boys?A2004B2005C2006D2007
From the pair of linear equations in the following problems, and find their solutions graphically.
(i)10 students of Class X took pan in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
(ii)5 pencils and 7 pens together cost Rs 50, whereas 7 pencils and 5 pens together cost Rs 46. Find the cost of one pencil and that of one pen.
View SolutionFrom the pairs of linear equation in this problem and find its solution graphically 10 students class x took park in mathematics quize. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quize
View SolutionTen students of class X took part in Mathematics quiz. If the number of girls is 4 more than the number of boys. Represent this situation algebraically and graphically.
View SolutionIn class VI, there are 30 students. If the number of girls is 3 more than twice the number of boys, then the number of boys and girls are :
View SolutionIn a class of 60 students, the number of girls is one third the number of boys. Find the number of girls and boys in the class.
View SolutionThe number of boys and girls in a class are in the ratio 5:4. If the number of boys is 9 more than the number of girls, then number of boys is 9.
View SolutionIn a school, the number of girls is 50 more than the number of boy The total number of students is 1070. Find the number of girls.
View Solution
