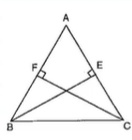
If D and E are points on sides AB and AC respectively of a ABC such that DEBC and BD=CE . Prove that ABC is isosceles.
To prove that triangle ABC is isosceles given the conditions, we can follow these steps:
Step 1: Understand the Given Information
We have triangle ABC with points D and E on sides AB and AC respectively. We know that DE is parallel to BC and that BD = CE.
Step 2: Apply the Basic Proportionality Theorem
Since DE is parallel to BC, by the Basic Proportionality Theorem (also known as Thales' theorem), we can write the following proportion:
ADDB=AEEC
Step 3: Use the Given Condition
From the problem, we know that BD = CE. Let's denote this common length as x. Therefore, we can write:
DB=xandEC=x
Step 4: Substitute in the Proportion
Substituting the values of DB and EC into the proportion gives us:
ADx=AEx
Step 5: Simplify the Equation
Since x is common in both denominators, we can cancel it out (assuming x ≠ 0):
AD=AE
Step 6: Conclude that Triangle ABC is Isosceles
Since AD = AE, we can conclude that triangle ABC has two sides (AB and AC) that are equal in length. Therefore, triangle ABC is isosceles.
Final Statement
Thus, we have proved that triangle ABC is isosceles.
---
We have triangle ABC with points D and E on sides AB and AC respectively. We know that DE is parallel to BC and that BD = CE.
Since DE is parallel to BC, by the Basic Proportionality Theorem (also known as Thales' theorem), we can write the following proportion:
ADDB=AEEC
From the problem, we know that BD = CE. Let's denote this common length as x. Therefore, we can write:
DB=xandEC=x
Substituting the values of DB and EC into the proportion gives us:
ADx=AEx
Since x is common in both denominators, we can cancel it out (assuming x ≠ 0):
AD=AE
Since AD = AE, we can conclude that triangle ABC has two sides (AB and AC) that are equal in length. Therefore, triangle ABC is isosceles.
Thus, we have proved that triangle ABC is isosceles.
Topper's Solved these Questions
Similar Questions
Knowledge Check
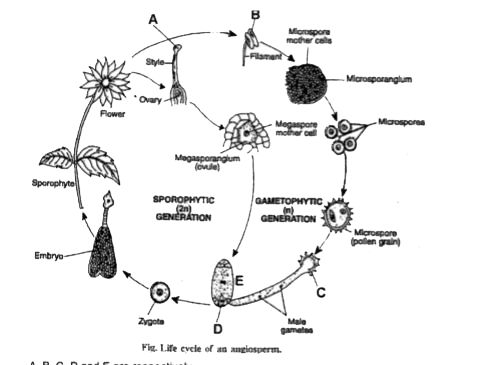
A, B, C, D and E are respectively -AStigma, Anther, Male gametophyte, Egg and Female gametophyteBStigma, Anther, Female gametophyte, Egg and Male gametophyteCStigma, Anther, Male gametophyte, Fertilized egg and Female gametophyteDStigma, Anther, Embryo sac, Egg and Female gametophyte
In Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD

View SolutionIn Figure, it is given that AE=AD and BD=CE. Prove that AEB≅ADC
View SolutionIn a ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DEBC : AB=12 cm, AD=8 cm, AE=12 cm and AC=18 cm . (ii) AB=5.6 cm, AD=1.4 cm, AC=7.2 cm and AE=1.8 cm
View SolutionIn a ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DEBC : AB=10.8cm, BD=4.5 cm, AC=4.8cm and AE=2.8cm (ii) AD=5.7cm, BD=9.5cm, AE=3.3cm and EC=5.5cm .
View SolutionIn a ABC , D and E are points on the sides AB and AC respectively such that DEBC If AD=4 , AE=8 , DB=x−4 , and EC=3x−19 , find x (ii) If AD=8 cm , AB=12cm and AE=12 cm , find CE . (iii) If AD=4 cm , DB=4.5 cm and AE=8 cm , find AC .
View SolutionD, E, F are the mid-points of the sides BC, CA and AB respectively of a ABC . Determine the ratio of the areas of DEF and ABC .
View SolutionDandE are points on equal sides ABandAC of an isosceles triangle ABC such that AD=AE . Prove that B,C,D,E are concylic.
View Solution