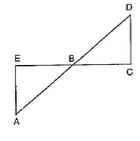
In Fig. 4.143, ∠A=∠CED , prove that CABCED . Also, find the value of x . (FIGURE)
To solve the problem, we need to prove that triangle CAB is similar to triangle CED and find the value of x.
Step 1: Identify the angles
We are given that ∠A=∠CED. Additionally, since both triangles share angle C, we have:
- ∠C=∠C (common angle)
We are given that ∠A=∠CED. Additionally, since both triangles share angle C, we have:
- ∠C=∠C (common angle)
Topper's Solved these Questions
Similar Questions
In Fig. 4.143, ∠A=∠CED , prove that CABCED . Also, find the value of x . (FIGURE)
View SolutionIn Fig. 4.97, if ∠A=∠C , then prove that AOB~COD . (FIGURE)
View SolutionIn Figure, ∠E>∠A and ∠C>∠D . Prove that AD>EC
View SolutionIn Fig. 4.124, E is a point on side CB produced of an isosceles triangle ABC with AB=AC . If AD⊥BC and EF⊥AC , prove that (i) ABDECF (ii) AB×EF=AD×EC . (FIGURE)
View SolutionIn Fig. 4.128, DEFG is a square and ∠BAC=90o . Prove that AGFDBG (ii) AGFEFC (FIGURE) (iii) DBGEFC (iv) DE2=BD×EC
View SolutionIn Fig. 4.144, we have ABCDEF . If AB=6cm , CD=x cm , EF=10cm , BD=4cm and DE=y cm , calculate the values of x and y . (FIGURE)
View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD

View SolutionIn Fig. 4.178, DEBC (FIGURE) If DE=4cm , BC=6cm and Area (ADE)=16 cm2 , find the area of ABC . (ii) If DE=4cm, BC=8cm and Area (ADE)=25 cm2 , find the area of ABC . (iii) If DE:BC=3:5 . Calculate the ratio of the areas of ADE and the trapezium BCED .
View SolutionIn Fig. 10.78, if AD, AE and BC are tangents to the circle at D, E and F respectively. Then, (FIGURE) AD=AB+BC+CA (b) 2AD=AB+BC+CA (c) 3AD=AB+BC+CA (d) 4AD=AB+BC+CA
View SolutionIn a ABC , D and E are points on the sides AB and AC respectively such that DEBC If AD=8x−7, DB=5x−3, AE=4x−3 and EC=(3x−1) , find the value of x . (ii) If AD=4x−3, AE=8x−7, BD=3x−1 and CE=5x−3 , find the volume x . (iii) If AD=2.5 cm , BD=3.0 cm and AE=3.75 cm , find the length of AC .
View Solution
