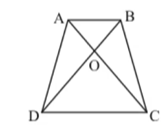
Diagonals AC and BD of a trapezium ABCD with ABDC intersect each other at the point O . Using similarity criterion for two triangles, show that OAOC=OBOD .
Step by step video & image solution for Diagonals A C and B D of a trapezium A B C D with A B D C intersect each other at the point O . Using similarity criterion for two triangles, show that (O A)/(O C)=(O B)/(O D) . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that OAOC=OBOD
View SolutionDiagonals AC and BD of a trapezium ABCD with ABDC intersect each other at the point O . Using similarity criterion for two triangles, show that OAOC=OBOD .
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(AOD)=ar(BOC) . Prove that ABCD is a trapezium.
View SolutionIf the diagonals AC,BD of a quadrilateral ABCD, intersect at O, and seqarate the quadrilateral into four triangles of equal area, show that quadrilateral ABCD is a parallelogram. GIVEN : A quadrilateral ABCD such that its diagonals AC and BD intersect at O and separate it into four parts such that ar(AOB)=ar(BOC)=ar(COD)=ar(AOD) TO PROVE : Quadrilateral ABCD is a parallelogram.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD)=ar ( BOC). Prove that ABCD is a trapezium.
View SolutionIn an isosceles triangle ABC, with AB=AC, the bisectors of B and C intersect each other at O. Join A to O. Show that :
(i) OB=OC
(ii) AO bisects A
View SolutionThe diagonals of quadrilateral ABCD,ACandBD intersect in O. Prove that if BO=OD, the triangles ABCandADC are equal in area.
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣CD . Prove that: ar(AOD)=ar(BOC).
View SolutionIn figure ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)=AODO.

View SolutionA point O is taken inside an equilateral four sided figure ABCD such that its distances from the angular points D and B are equal. Show that AO and OC are in one and the same straight line. GIVEN : A point O inside an equilateral quadrilateral four sided figure ABCD such that BO=OD. TO PROVE : AO and OC are in one and the same straight line.
View Solution
