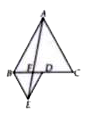
In figure ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)=AODO.

△ABC and △DBC are two triangles on the same base BC. If AD intersects BC at O.
To Prove:
Ar(ΔABC)Ar(ΔDBC)=AODO
Construction: Drawn AP⊥BCand DM⊥BC.
Areaof△=12×base×height
ArΔABCAr(ΔDBC)=12×BC×DM12×BC×AP=APDM
In △APO and △DMO,
∠APO=∠DMO=90∘
(construction)
∠AOP=∠DOM (Vertically opposite angles)
∴△APO∼△DMO
(Similarity criterion is AAA.)
⇒Ar(ΔABC)Ar(ΔDBC)=AODO
(proved)
Similar Questions
In Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)= AODO
View SolutionIn the given figure, ΔABCandΔDBC are on the same base BC. If AD intersects BC at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
View SolutionIn the same figure, ΔABCandΔDBC are on the same base BC . If AD is intersects BC at O, prove that
ar(ΔABC)ar(ΔDBC)=AODO
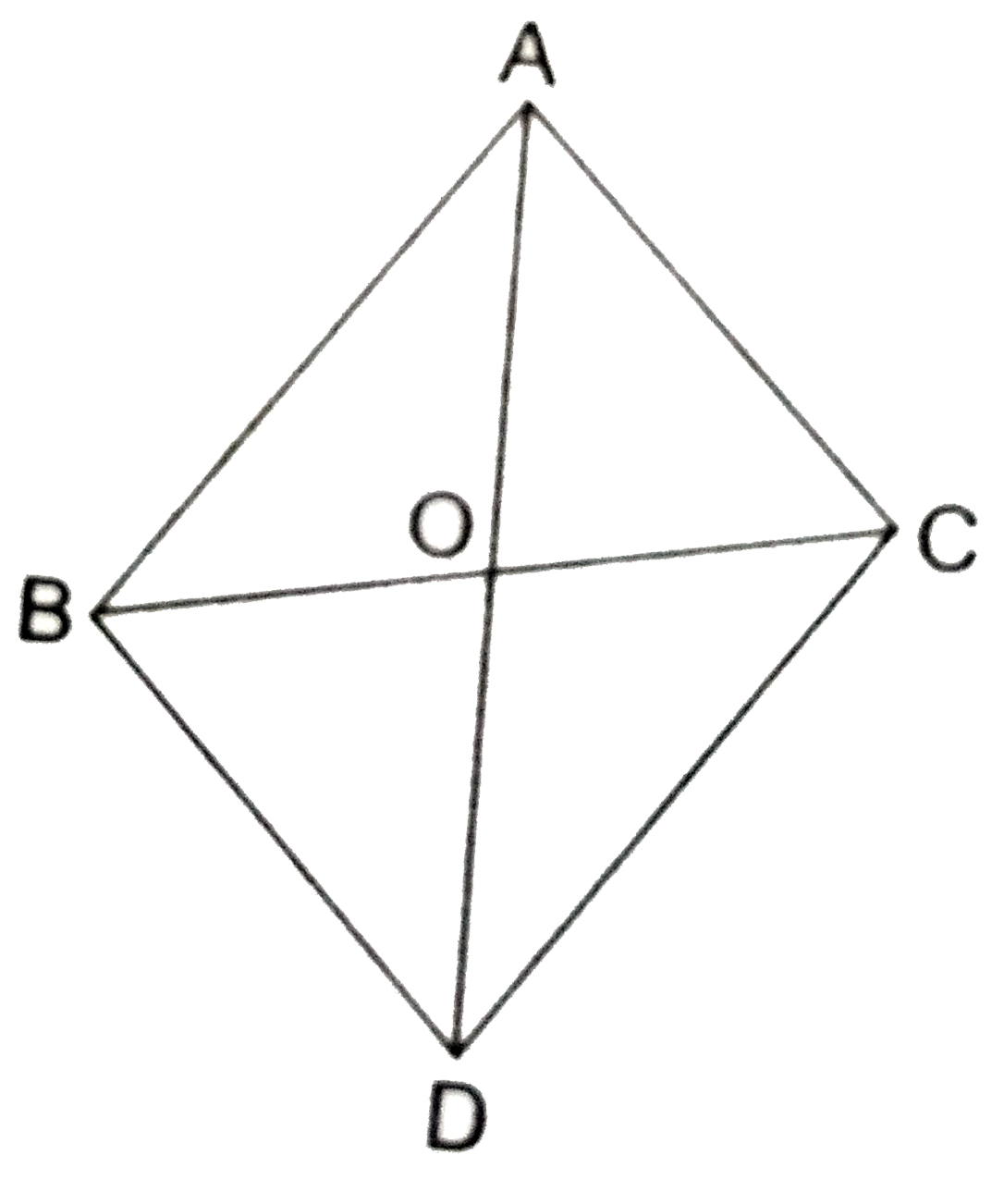
View SolutionIn the given figure, ΔABCandΔDBC have the same base BC. If AD and BC intersect at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
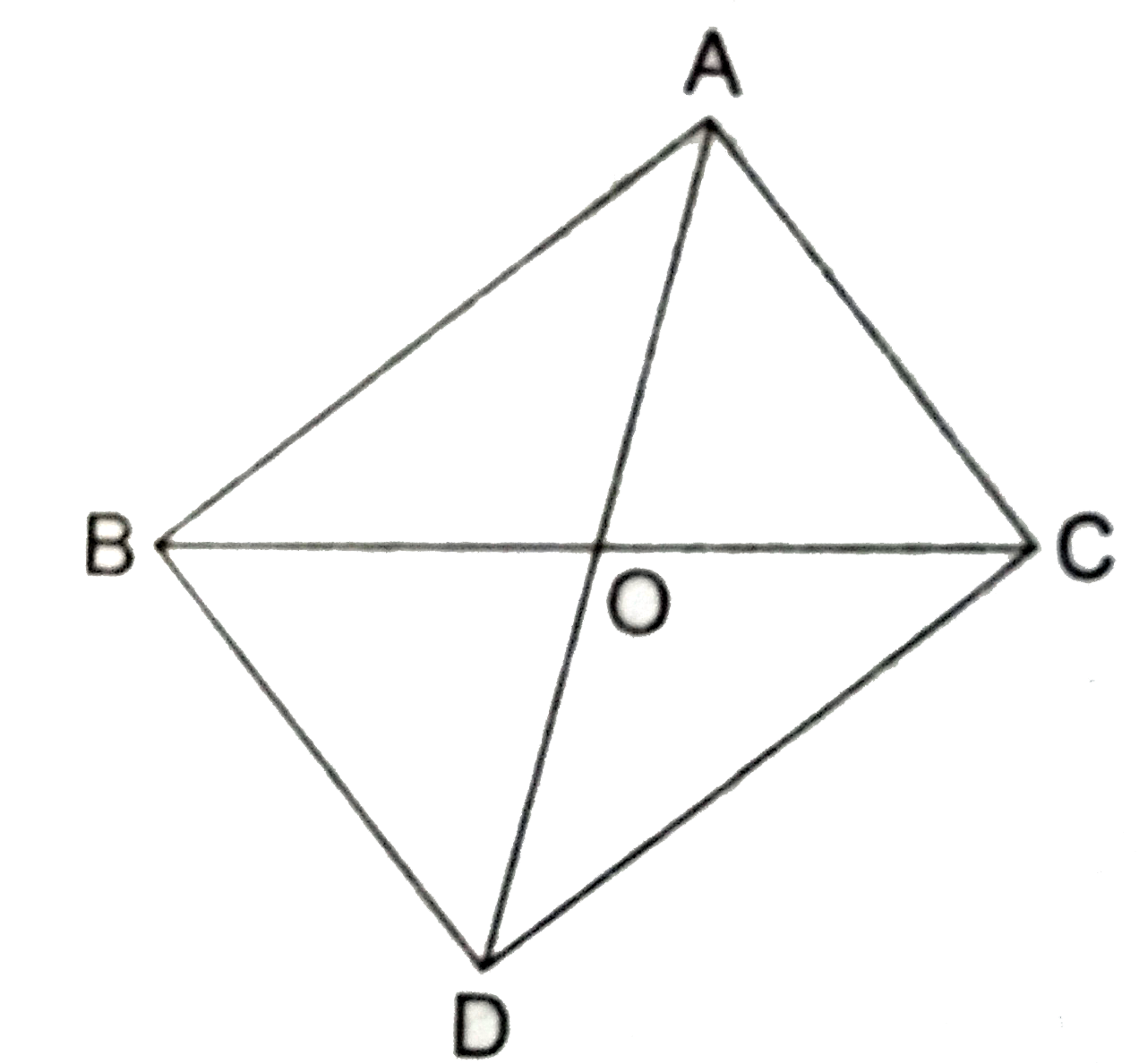
View SolutionIn Fig. 4.179, ABC and DBC are on the same base BC . If AD and BC intersect at O , prove that Area (ABC)Area (DBC)=AODO (FIGURE)
View SolutionIn Figure, ABC and DBC are two triangles on the same base BC such that AB=AC and DB=DC. Prove that ∠ABD=∠ACD
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
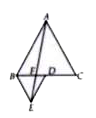
ar(ΔBDE) = 1/4 ar(ΔABC)
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
ar(ΔABC) = 2 ar(ΔBEC)
View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD

View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).

View Solution
