In ABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ADE and ABC .
To find the ratio of the areas of triangle ADE and triangle ABC, we can follow these steps:
Step 1: Identify the midpoints
Given triangle ABC, points D and E are the midpoints of sides AB and AC respectively.
Step 2: Establish parallel lines
Since D and E are midpoints, the line segment DE is parallel to side BC of triangle ABC. This is a property of triangles where the line segment joining the midpoints of two sides is parallel to the third side.
Step 3: Use properties of similar triangles
Because DE is parallel to BC, triangles ADE and ABC are similar by the Basic Proportionality Theorem (also known as Thales' theorem). This means that the corresponding angles of triangles ADE and ABC are equal:
- ∠ADE=∠ABC
- ∠ADE=∠ACB
- ∠A=∠A (common angle)
Step 4: Establish the ratio of corresponding sides
Since D and E are midpoints, we can say:
- AD=12AB
- AE=12AC
Thus, the ratio of the corresponding sides AD to AB is:
ADAB=12
Step 5: Calculate the ratio of the areas
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can write:
Area of △ADEArea of △ABC=(ADAB)2=(12)2=14
Step 6: Express the ratio in simplest form
Thus, the ratio of the areas of triangle ADE to triangle ABC is:
Area of △ADE:Area of △ABC=1:4
Final Answer
The ratio of the areas of triangle ADE and triangle ABC is 1:4.
---
Given triangle ABC, points D and E are the midpoints of sides AB and AC respectively.
Since D and E are midpoints, the line segment DE is parallel to side BC of triangle ABC. This is a property of triangles where the line segment joining the midpoints of two sides is parallel to the third side.
Because DE is parallel to BC, triangles ADE and ABC are similar by the Basic Proportionality Theorem (also known as Thales' theorem). This means that the corresponding angles of triangles ADE and ABC are equal:
- ∠ADE=∠ABC
- ∠ADE=∠ACB
- ∠A=∠A (common angle)
Since D and E are midpoints, we can say:
- AD=12AB
- AE=12AC
ADAB=12
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can write:
Area of △ADEArea of △ABC=(ADAB)2=(12)2=14
Thus, the ratio of the areas of triangle ADE to triangle ABC is:
Area of △ADE:Area of △ABC=1:4
The ratio of the areas of triangle ADE and triangle ABC is 1:4.
Topper's Solved these Questions
Similar Questions
D, E, F are the mid-points of the sides BC, CA and AB respectively of a ABC . Determine the ratio of the areas of DEF and ABC .
View SolutionIn a ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DEBC : AB=12 cm, AD=8 cm, AE=12 cm and AC=18 cm . (ii) AB=5.6 cm, AD=1.4 cm, AC=7.2 cm and AE=1.8 cm
View Solution
Knowledge Check
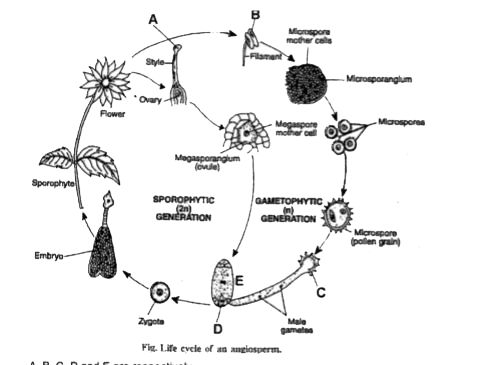
A, B, C, D and E are respectively -AStigma, Anther, Male gametophyte, Egg and Female gametophyteBStigma, Anther, Female gametophyte, Egg and Male gametophyteCStigma, Anther, Male gametophyte, Fertilized egg and Female gametophyteDStigma, Anther, Embryo sac, Egg and Female gametophyte
In Figure, triangle ABC is right-angled at B. Give that AB=9CM, AC=15CM,andD,E are the mid-points of the sides ABandAC respectively, calculate
The length of BC
(ii) The area of ADE
View SolutionIn a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View SolutionABC is an isosceles triangle in which AB=AC. If DandE are the mid-points of ABandAC respectively, prove that the points B,C,DandE are concylic.
View SolutionABC is an isosceles triangle in which AB=AC. If D and E are the mid-points of AB and AC respectively, prove that the points B, C, D and E are concyclic.
View SolutionABCD is a trapezium with parallel sides AB=a and DC=b. If EandF are mid-points of non-parallel sides ADandBC respectively, then the ratio of areas of quadrilaterals ABFEandEFCD is:
(a) a:b
(b) (a+3b):(3a+b)
(c) (3a+b):(a+3b)
(d) (3a+b):(3a+b)
View SolutionIn a ABC , D and E are points on AB and AC respectively such that DE/BC . If AD=2.4cm, AE=3.2cm, DE=2cm and BC=5cm , find BD and CE .
View SolutionIn Fig. 32, ABCD is a rectangle of length AB=40 cm and breadth BC=25 cm. If P,Q,R,S be the mid-points of the sides AB, BC, CD and DA respectively, find the area of the shaded region.
View Solution
