(Result on acute triangle) In Fig. 4.184, ∠B of ABC is an acute angle and AD⊥BC , prove that AC2=AB2+BC2−2 BC×BD
To prove that AC2=AB2+BC2−2⋅BC⋅BD given that AD⊥BC in triangle ABC where ∠B is an acute angle, we can follow these steps:
Step 1: Identify the right triangles
Since AD is perpendicular to BC, we can analyze two right triangles: △ABD and △ADC.
Step 2: Apply the Pythagorean theorem to triangle ABD
In triangle ABD:
AB2=AD2+BD2(1)
Step 3: Apply the Pythagorean theorem to triangle ADC
In triangle ADC:
AC2=AD2+DC2(2)
Step 4: Express DC in terms of BC and BD
Since D is a point on BC, we have:
DC=BC−BD
Step 5: Substitute DC into equation (2)
Substituting DC into equation (2):
AC2=AD2+(BC−BD)2
Step 6: Expand the squared term
Now, expand (BC−BD)2:
(BC−BD)2=BC2−2⋅BC⋅BD+BD2
Thus,
AC2=AD2+BC2−2⋅BC⋅BD+BD2
Step 7: Combine terms
Now we can combine terms:
AC2=AD2+BD2+BC2−2⋅BC⋅BD
Step 8: Substitute AD2+BD2 from equation (1)
From equation (1), we know:
AD2+BD2=AB2
Substituting this into our equation gives:
AC2=AB2+BC2−2⋅BC⋅BD
Conclusion
Thus, we have proved that:
AC2=AB2+BC2−2⋅BC⋅BD
Since AD is perpendicular to BC, we can analyze two right triangles: △ABD and △ADC.
In triangle ABD:
AB2=AD2+BD2(1)
In triangle ADC:
AC2=AD2+DC2(2)
Since D is a point on BC, we have:
DC=BC−BD
Substituting DC into equation (2):
AC2=AD2+(BC−BD)2
Now, expand (BC−BD)2:
(BC−BD)2=BC2−2⋅BC⋅BD+BD2
Thus,
AC2=AD2+BC2−2⋅BC⋅BD+BD2
Now we can combine terms:
AC2=AD2+BD2+BC2−2⋅BC⋅BD
From equation (1), we know:
AD2+BD2=AB2
Substituting this into our equation gives:
AC2=AB2+BC2−2⋅BC⋅BD
Thus, we have proved that:
AC2=AB2+BC2−2⋅BC⋅BD
Topper's Solved these Questions
Similar Questions
Knowledge Check
In an acute-angled triangle ABC if sin (B+C−A)=√32 and tan(C+A−B)=1, then C is equal to
A37.5∘B67.5∘C52.5∘D72.5∘
In figure, ABC is triangle in which ∠ABC=90∘and AD⊥CBproduced. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionIn ABC , AD is a median. Prove that AB2+AC2=2 AD2+2 DC2 .
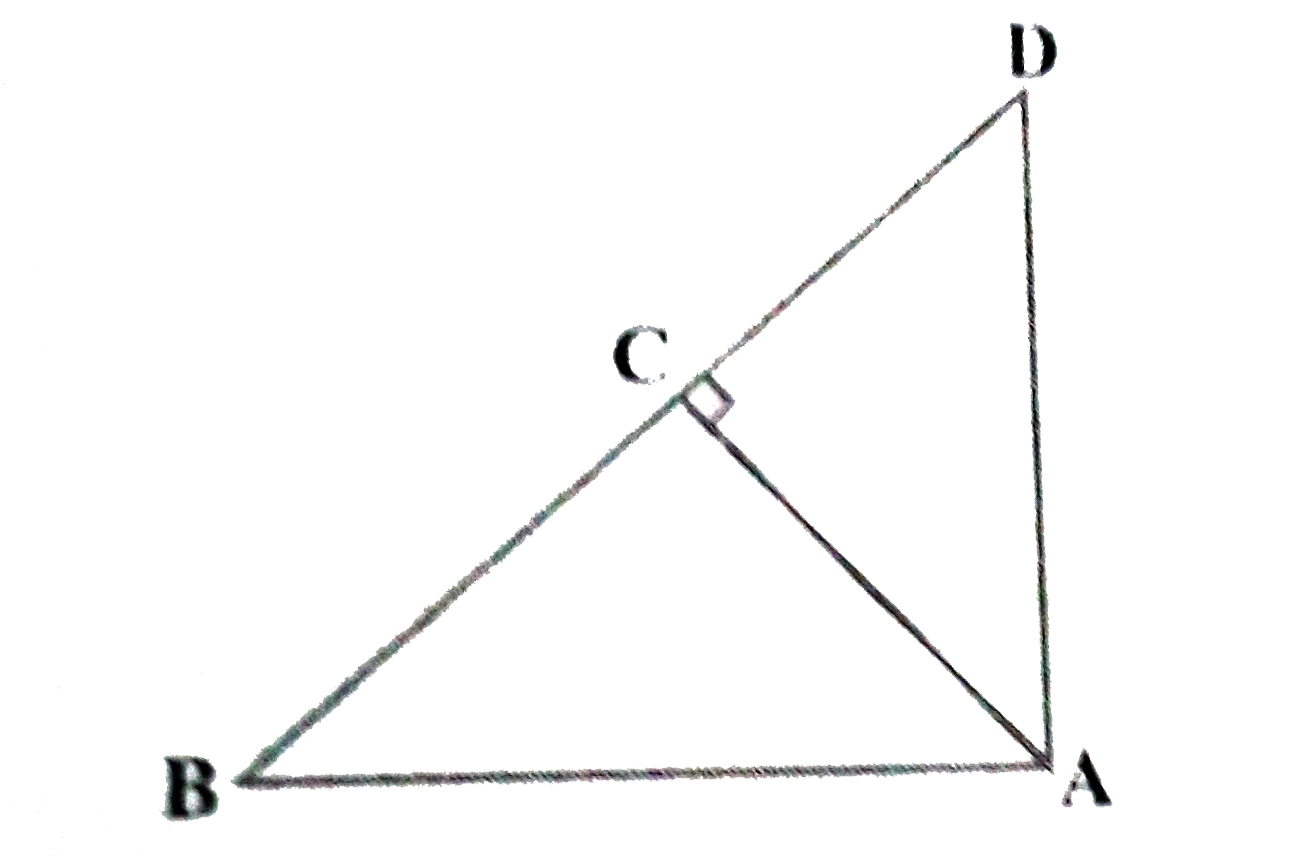
View SolutionIn Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
View SolutionIn a quadrilateral ABCD , given that ∠A+∠D=90o . Prove that AC2+BD2=AD2+BC2 .
View SolutionIn Fig. 5.10, if AC=BD, then prove that AB=CD.

View SolutionIn an equilateral triangle ABC if AD⊥BC, then AD2 = (a)CD2 (b) 2CD2 (c) 3CD2 (d) 4CD2
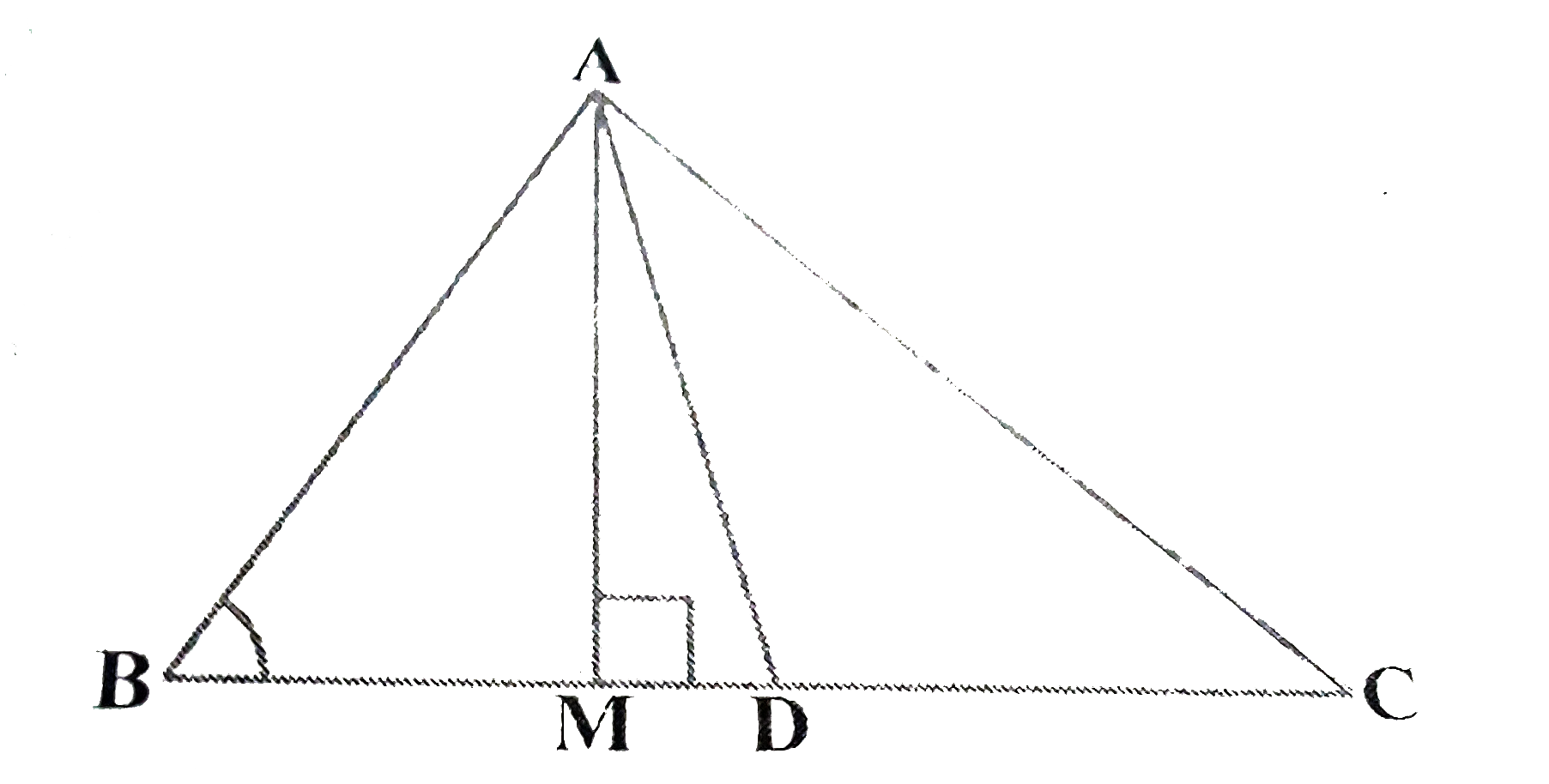
View SolutionIn figure, AD is a median of a triangle ABC and AM⊥BC. Prove that:
(i) AC2=AD2+BC.DM+(BC2)2
(ii) AB2=AD2−BC.DM+(BC2)2
(iii) AC2+AB2=2AD2+12BC2
View Solution

